Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
tvms_06_131206.ppt
Содержание
- 1. tvms_06_131206.ppt
- 2. ВОПРОС 56:МЕТОД МОНТЕ-КАРЛО (МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ)
- 3. Метод статистических испытаний
- 4. ВОПРОС 57:Оценка погрешности метода Монте-Карло
- 5. Определить число δ:- задача определения доверительного интервалаСлучай
- 6. Случай 2.где tγ – из таблиц распределения Стьюдента по входным параметрам n и γ,
- 7. Случай 3.
- 8. Разыгрывание случайных величин
- 9. ВОПРОС 58:Разыгрывание дискретныхслучайных величин
- 10. Определение. Случайными числами называют возможные значения r
- 11. Разыгрывание дискретной случайной величины Задача. Построить реализацию
- 12. 01p1+p2p1p1+p2+…+pn-1…Теорема. 010101010…10…10Генерируемая с.в. соответствует закону распределения F(x)
- 13. Пример. Разыграть 10 значений дискретной случайной величины
- 14. Разыгрывание противоположных событий Пример. 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34.
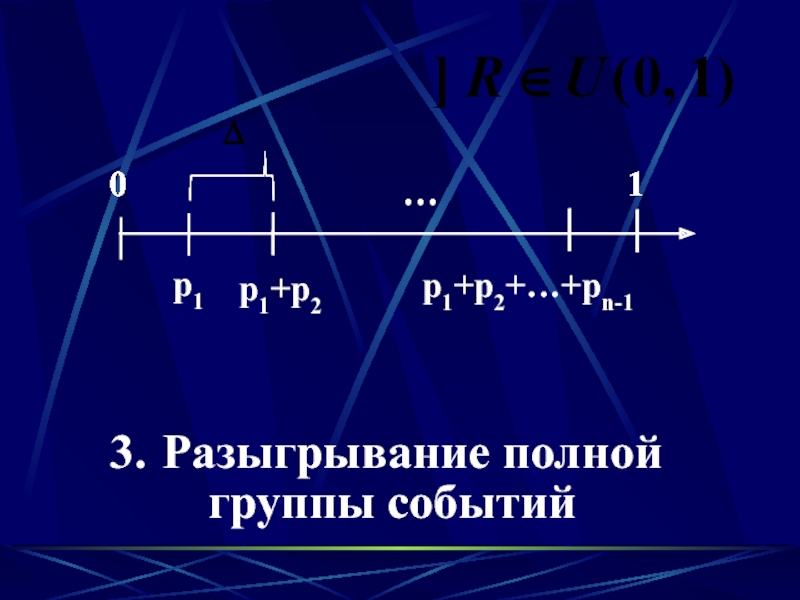
- 15. 01p1+p2p1p1+p2+…+pn-1…010101010…10…10Разыгрывание полной группы событий
- 16. ВОПРОС 59:Разыгрывание непрерывныхслучайных величин
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Метод суперпозиции ➪т.к. при х→∞ F(x) → 1
- 21. ] Z – c.в.: Z:
- 22. Приближенное разыгрывание нормальной случайной величины ➪n = 12:
- 23. В силу центральной предельной теоремы ➪При n=12:
- 24. КОРРЕЛЯЦИОННЫЙИ РЕГРЕССИОННЫЙ АНАЛИЗ
- 25. ВОПРОС 60:Статистические зависимости
- 26. ЗАВИСИМОСТИФункциональныеСтатистическиеОпределение:Две случайные величины и находятся в статистической
- 27. ВОПРОС 61:Коэффициент корреляции
- 28. Определение:Определение:Две случайные величины независимы, если для них
- 29. Свойства:1. Для независимых случайных величин коэффициент корреляции равен нулю:2.
- 30. - нормально-распределенной с.в.
- 31. Функции и линии регрессии ВОПРОС 62:
- 32. Определение:- зависимые случайные величины: называется условной плотностью распределения с.в.
- 33. Определение:Условным математическим ожиданием называется Функция
- 34. Аналогично:Условным математическим ожиданием называется Функция
- 35. Слайд 35
- 36. Аналогично:Здесь - коэффициенты регрессии
- 37. ВОПРОС 63:Анализ линейной зависимости по опытным данным
- 38. (x1, y1), (x2, y2), ..., (xi, yi), ..., (xn, yn)
- 39. Определение:Выборочными коэффициентом корреляции называется число
- 40. Оценки коэффициентов регрессии:
- 41. Уравнения эмпирических прямых регрессий
- 42. Проверка гипотезы о значимости выборочного коэффициента корреляции ВОПРОС 64:
- 43. Н0: rn=0 Н1: rn ≠ 0 α
- 44. ВОПРОС 65:Ранговая корреляция
- 45. ] выборка объема n содержит независимые объекты
- 46. Две последовательности рангов: по признаку А:
- 47. ,
- 48. Свойства выборочного коэффициента корреляции Спирмена1. A=kB
- 49. Н1: ρS ≠ 0. Н0: ρS =
- 50. Выборочный коэффициент ранговой корреляции Кендалла
- 51. Спасибо за внимание!
- 52. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5
Определить число δ:
- задача определения доверительного интервала
Случай 1.
где t –
аргумент функции Лапласа, при котором Ф(t) = γ/2.
Слайд 10
Определение. Случайными числами называют возможные значения r непрерывной случайной величины
R, распределенной равномерно в интервале
Слайд 11Разыгрывание дискретной
случайной величины
Задача. Построить реализацию с.в. X с
известным законом распределения F(x):
Х х1 х2 … хn
F р1 р2 … рn
Слайд 12
0
1
p1+p2
p1
p1+p2+…+pn-1
…
Теорема.
0
1
0
1
0
1
0
1
0
…
1
0
…
1
0
Генерируемая с.в. соответствует
закону распределения F(x)
Слайд 13Пример.
Разыграть 10 значений дискретной случайной величины Х, закон распределения
которой имеет вид: Х 2
3 6 8P 0,1 0,3 0,5 0,1
Решение. Разобьем интервал (0, 1) на частичные интервалы: Δ1- (0; 0,1), Δ2 – (0,1; 0,4), Δ3 - (0,4; 0,9), Δ4 – (0,9; 1).
Выпишем из таблицы случайных чисел 10 чисел: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34. Первое и седьмое числа лежат на интервале Δ1, следовательно, в этих случаях разыгрываемая случайная величина приняла значение х1 = 2; третье, четвертое, восьмое и десятое числа попали в интервал Δ2, что соответствует х2 = 3; второе, пятое, шестое и девятое числа оказались в интервале Δ3 – при этом Х = х3 = 6; на последний интервал не попало ни одного числа. Итак, разыгранные возможные значения Х таковы: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.
Слайд 14
Разыгрывание противоположных событий
Пример.
0,09; 0,73; 0,25; 0,33; 0,76; 0,52;
0,01; 0,35; 0,86; 0,34.
Слайд 21] Z – c.в.: Z: 1
2
P: C1 C2Если Z=1, то ищем искомое возможное значение Х из уравнения
а если Z=2, то решаем уравнение
Слайд 26ЗАВИСИМОСТИ
Функциональные
Статистические
Определение:
Две случайные величины и находятся в статистической (корреляционной) зависимости, если
каждому значению одной из этих величин соответствует определенное распределение вероятностей
другой.Слайд 28Определение:
Определение:
Две случайные величины независимы, если для них выполняется условие
Коэффициентом корреляции
двух случайных величин называется безразмерная мера связи (зависимости), определяемая соотношением
Слайд 32Определение:
- зависимые случайные величины:
называется условной плотностью распределения с.в.
Слайд 33Определение:
Условным математическим ожиданием называется
Функция
называется
функцией регрессии на , а ее
график - линией регрессии на .
Слайд 34Аналогично:
Условным математическим ожиданием называется
Функция
называется
функцией регрессии на , а ее
график - линией регрессии на .
Слайд 43
Н0: rn=0
Н1: rn ≠ 0
α – уровень
значимости
|Tнабл| < tкр – нулевая гипотеза принимается
(корреляции нет);
|Tнабл| >
tкр – нулевая гипотеза отвергается (корреляция есть).
Слайд 45] выборка объема n содержит независимые объекты
обладающие двумя качественными
признаками: А и В.
rang(O) = 1, rang(O) = 2,
…, rang(OСлайд 48Свойства выборочного коэффициента
корреляции Спирмена
1. A=kB
ρS=1.
2. A
не зависит от B
ρS=0.
3. В остальных случаях
-1<ρS <0
Слайд 49Н1: ρS ≠ 0.
Н0: ρS = 0.
k=n–2,
α
S(α,
k)
tкр(α, k)
| ρS | < Tкр,
Н0 не отвергается.
| ρS | > Tкр,
Н0 отвергается.
Слайд 50Выборочный коэффициент
ранговой корреляции Кендалла
R =R1 + R2 +…+ Rn-1
Ri - число рангов правее yi в
ряду y1,y2,…,yn



















![tvms_06_131206.ppt ] Z – c.в.: Z: 1 2 ] Z – c.в.: Z: 1 2](/img/thumbs/68bcc39be3251520959620e90f2ba7b7-800x.jpg)























![tvms_06_131206.ppt ] выборка объема n содержит независимые объекты обладающие двумя качественными признаками: ] выборка объема n содержит независимые объекты обладающие двумя качественными признаками: А и В. rang(O) = 1,](/img/thumbs/ae1c8504e48dfd80a57d747da52acfb1-800x.jpg)