Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тягово-скоростные свойства КМ с гидродинамической передачей Одним из основных
Содержание
- 1. Тягово-скоростные свойства КМ с гидродинамической передачей Одним из основных
- 2. Обеспечение оптимальных зависимостей изменения Mкр от оборотов
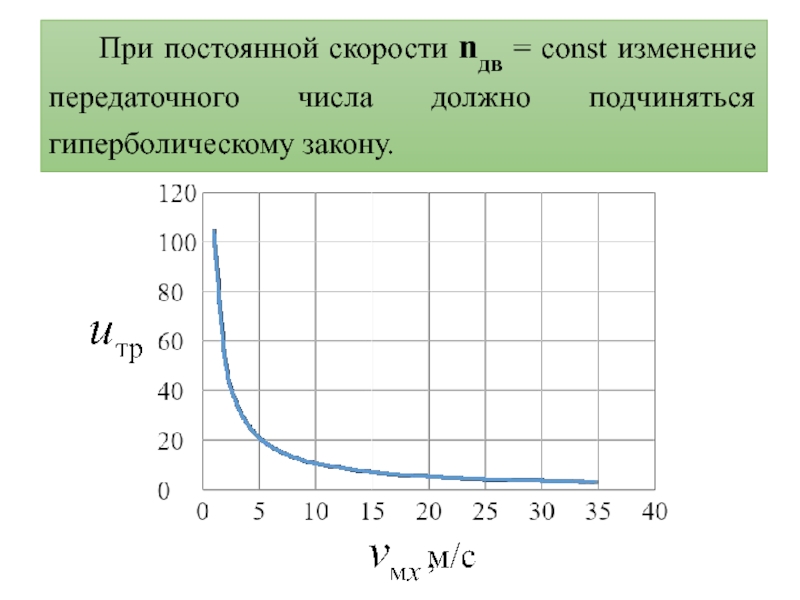
- 3. При постоянной скорости nдв = const изменение передаточного числа должно подчиняться гиперболическому закону.
- 4. Однако при малых скоростях движения и большом
- 5. Основные параметры гидродинамической передачи:Из бесступенчатых передач наибольшее
- 6. Основные параметры гидродинамической передачи:коэффициент трансформации Kгт =
- 7. Основные параметры гидродинамической передачи:коэффициент полезного действияηгт(iгт), Kгт(iгт), λнас(iгт)Энергетические параметры:Безразмерные характеристики:
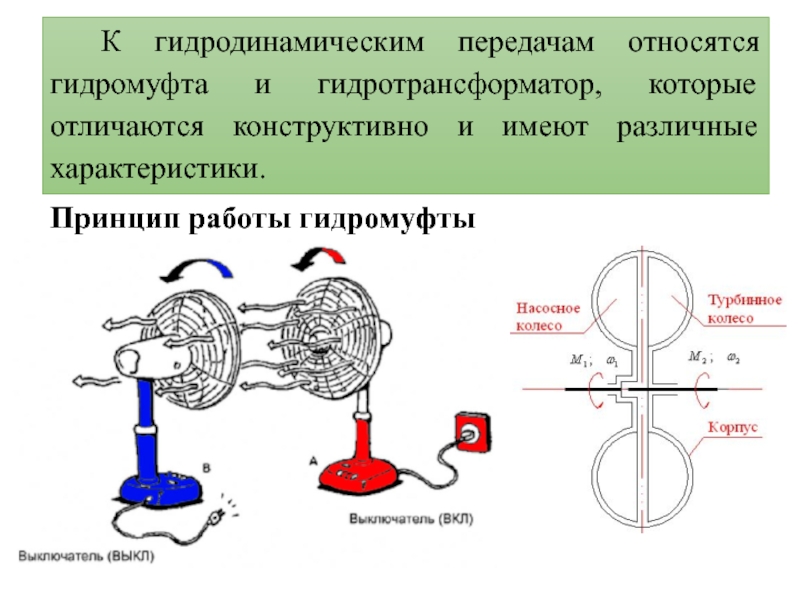
- 8. К гидродинамическим передачам относятся гидромуфта и гидротрансформатор, которые отличаются конструктивно и имеют различные характеристики.Принцип работы гидромуфты
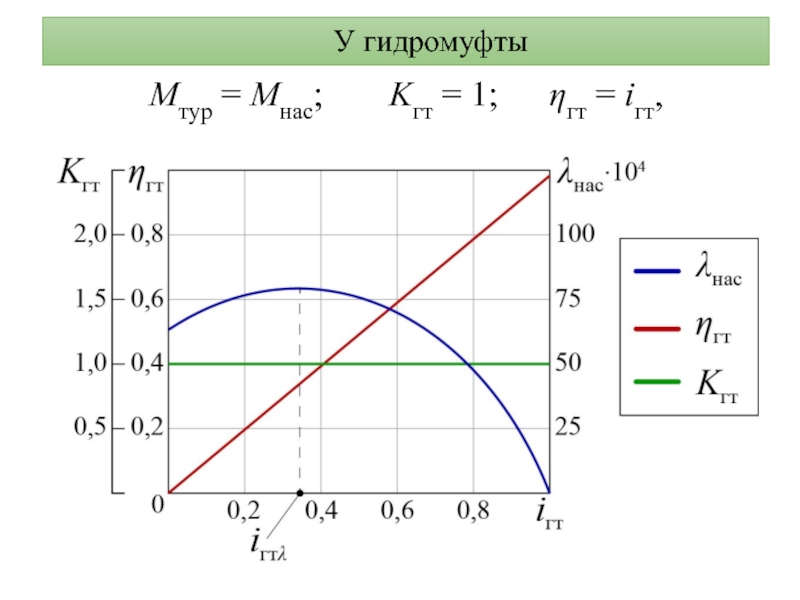
- 9. У гидромуфты Mтур = Mнас; Kгт = 1; ηгт = iгт,
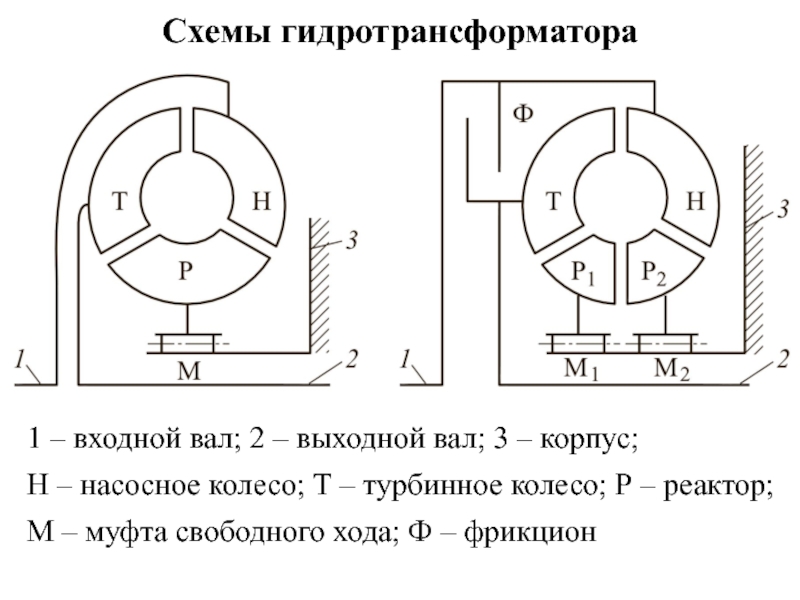
- 10. 1 – входной вал; 2 – выходной
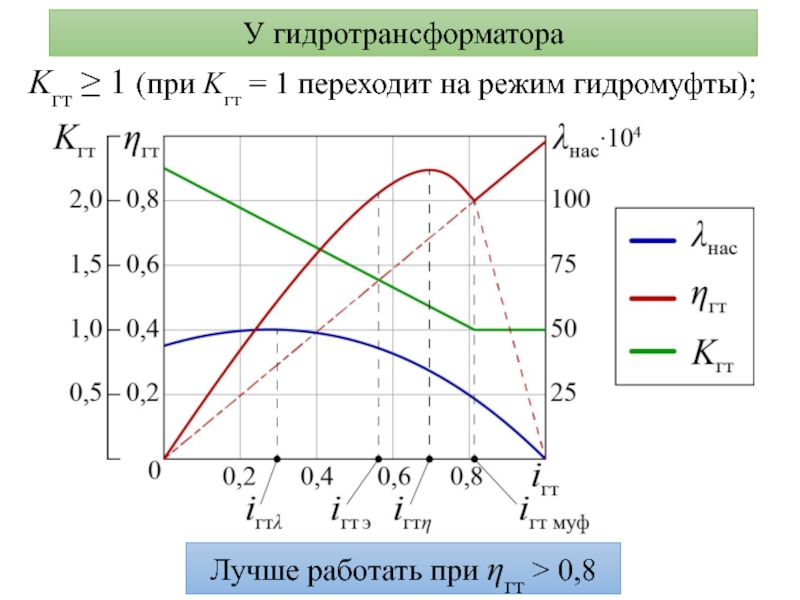
- 11. У гидротрансформатора Kгт ≥ 1 (при Kгт
- 12. Имеются следующие характерные точки:1. В стоповом режиме
- 13. Диапазон 0 ≤ iгт ≤ iгт э
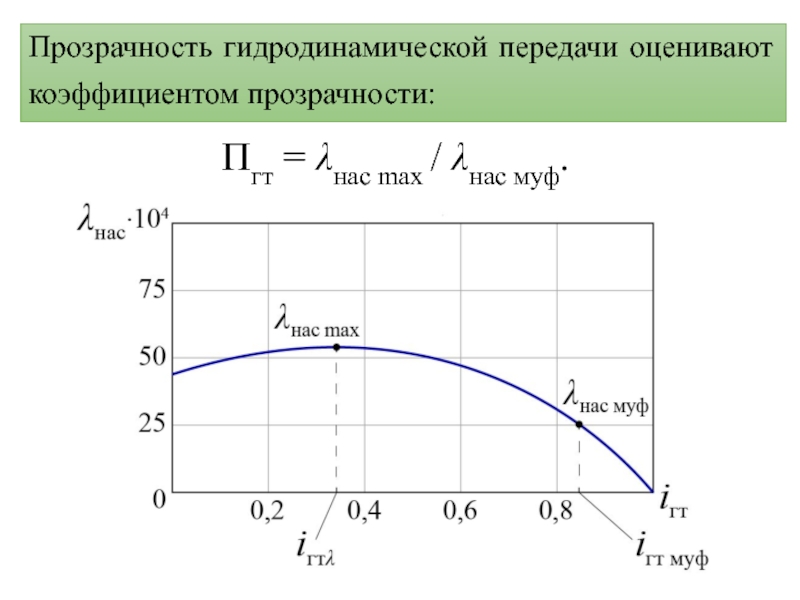
- 14. Прозрачность гидродинамической передачи оценивают коэффициентом прозрачности:Пгт = λнас max / λнас муф.
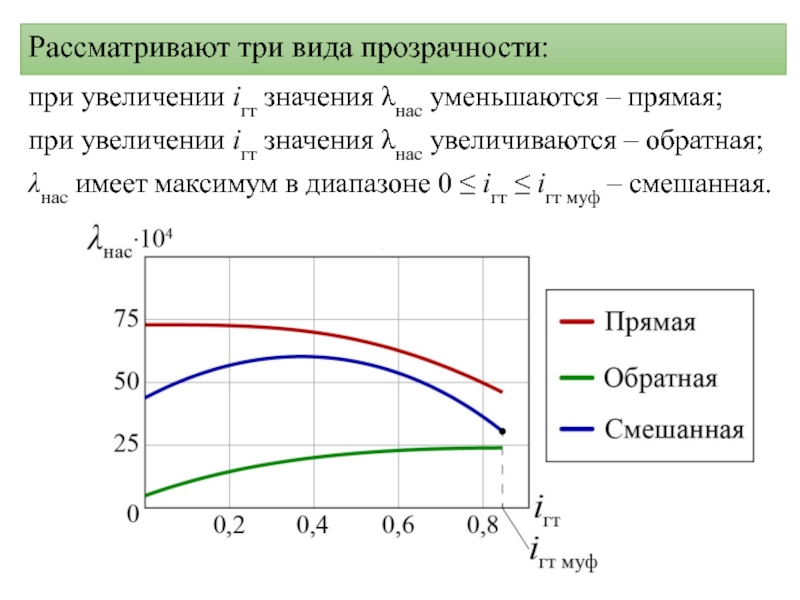
- 15. Рассматривают три вида прозрачности:при увеличении iгт значения
- 16. В зависимости от значения коэффициента прозрачности гидродинамические
- 17. Это объясняется тем, что эти передачи, в
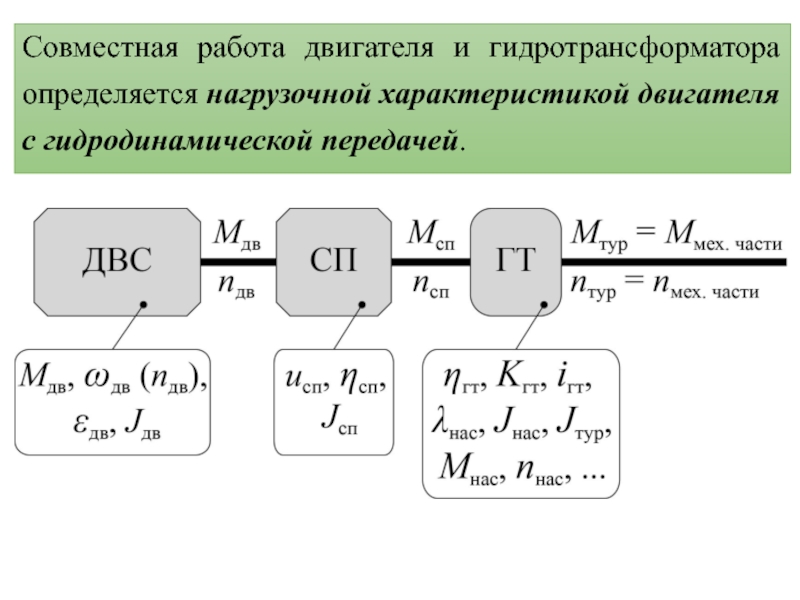
- 18. Совместная работа двигателя и гидротрансформатора определяется нагрузочной характеристикой двигателя с гидродинамической передачей.
- 19. Согласующая передача (СП) обеспечивает согласование оборотов двигателя и рабочих оборотов насосного колеса.
- 20. Для совместной работы необходимо, чтобы момент, поступающий
- 21. Пересечения кривых Mсп(nсп) и Mнас(nнас) при nсп
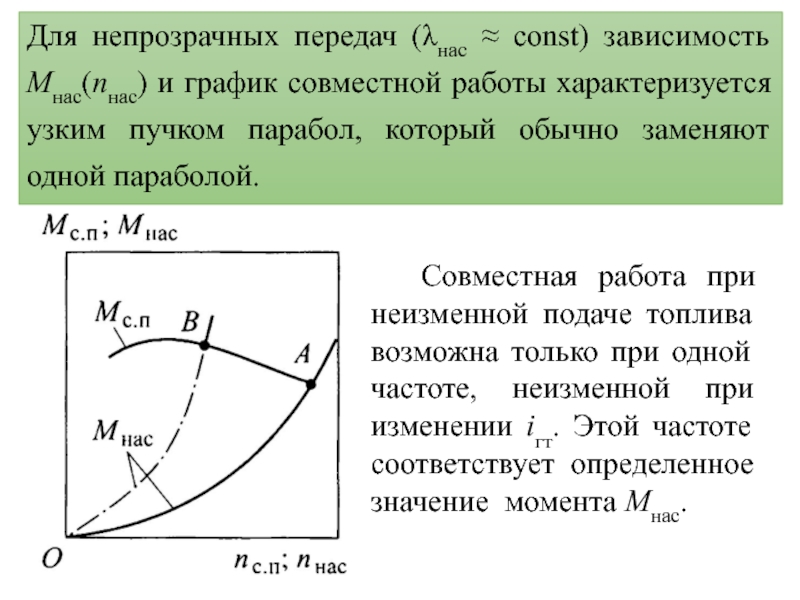
- 22. Для непрозрачных передач (λнас ≈ const) зависимость
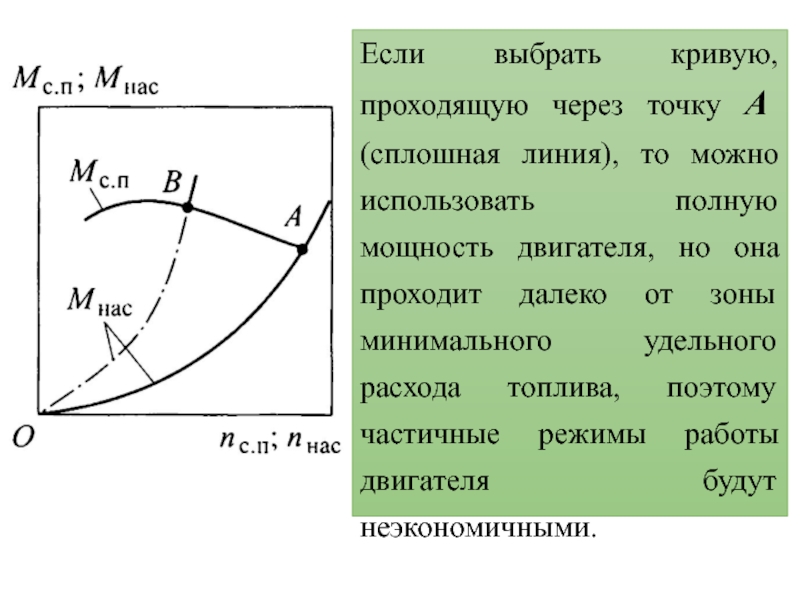
- 23. Если выбрать кривую, проходящую через точку A
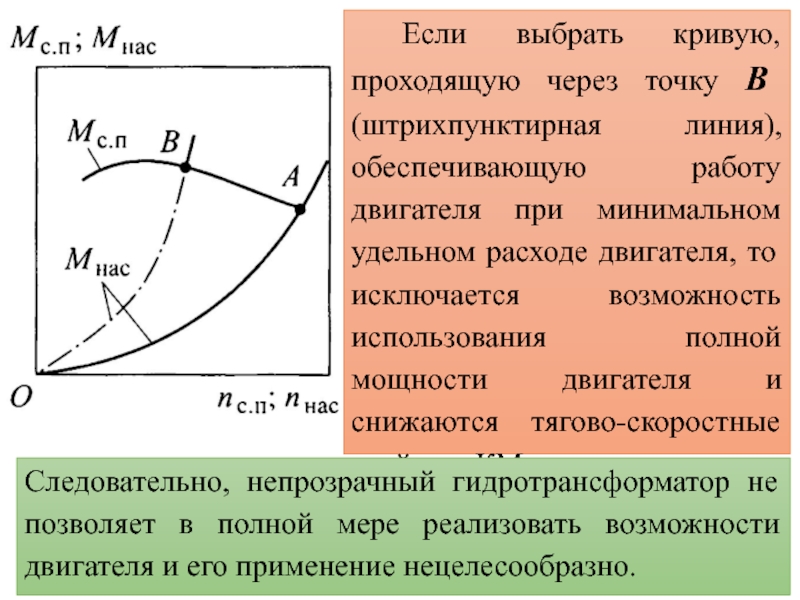
- 24. Если выбрать кривую, проходящую через точку B
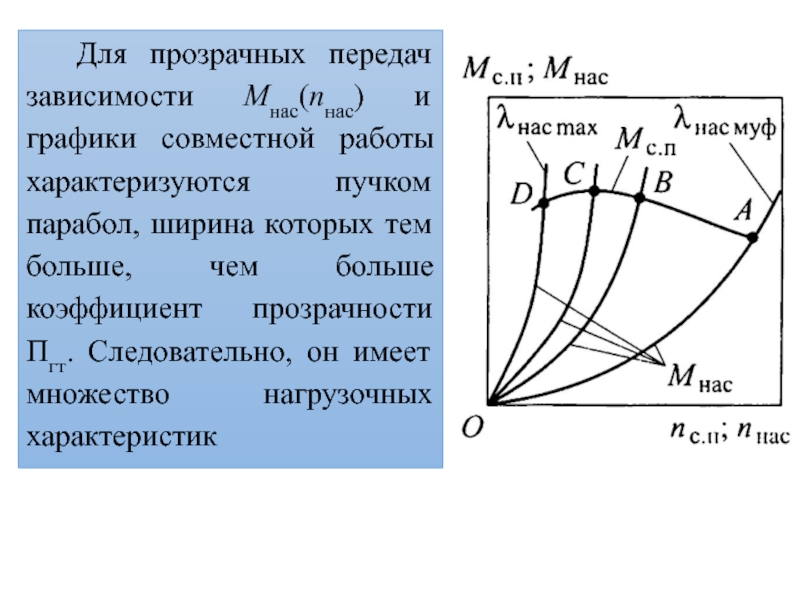
- 25. Для прозрачных передач зависимости Mнас(nнас) и графики
- 26. Точки пересечения кривых Mсп(nсп) и Mнас(nнас) при
- 27. Нагрузочная кривая, получаемая при λнас max, должна
- 28. Для определения динамической характеристики Dф(mм; vxм; uтр)
- 29. Параметры входного вала насосного колеса: nсп =
- 30. Определяются параметры на выходном валу турбинного колеса,
- 31. Дальнейший расчет аналогичен рассмотренному ранее расчету для
- 32. Дифференциальное уравнение прямолинейного движения КМ с гидромеханической
- 33. где Jспi – момент инерции i-й вращающейся
- 34. Суммарный инерционный момент двигателя, согласующей передачи и
- 35. Для непрозрачного гидротрансформатора dωнас / dt =
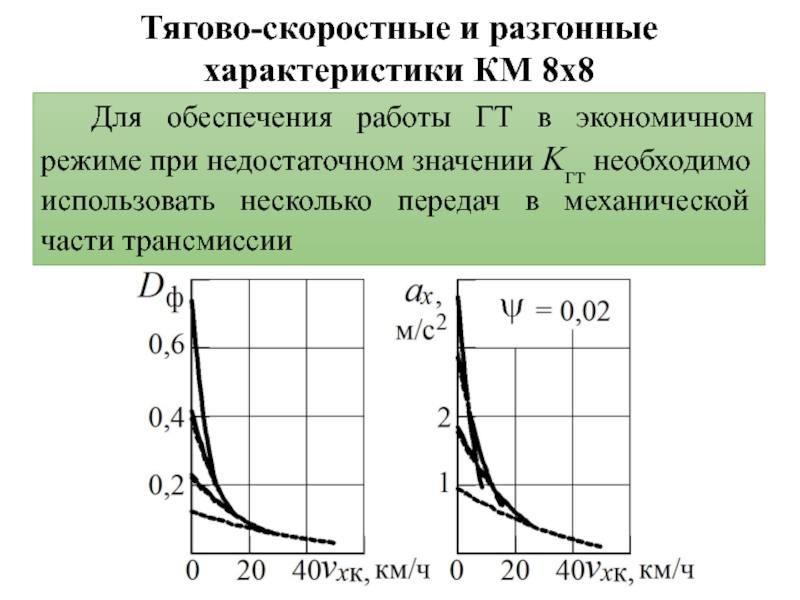
- 36. Тягово-скоростные и разгонные характеристики КМ 8х8Для обеспечения
- 37. Скачать презентанцию
Обеспечение оптимальных зависимостей изменения Mкр от оборотов на КД возможно за счет изменения передаточного числа в трансмиссии, которое может быть определено из уравнения:
Слайды и текст этой презентации
Слайд 1Тягово-скоростные свойства КМ с гидродинамической передачей
Одним из основных направлений частичной
Слайд 2Обеспечение оптимальных зависимостей изменения Mкр от оборотов на КД возможно
за счет изменения передаточного числа в трансмиссии, которое может быть
определено из уравнения:
Слайд 3При постоянной скорости nдв = const изменение передаточного числа должно
подчиняться гиперболическому закону.
Слайд 4Однако при малых скоростях движения и большом передаточном числе трансмиссии
момент на колесе ограничен предельной реакцией по сцеплению (Rx) должен
быть ограничен и диапазон передаточных чисел величиной uтр max.При изменении передаточного числа uтр по гиперболическому закону увеличивается скорость движения на предельных по мощности двигателя подъемах, возрастает ускорение при разгоне, уменьшается время и путь разгона.
Слайд 5Основные параметры гидродинамической передачи:
Из бесступенчатых передач наибольшее распространение получили гидродинамические.
передаточное
отношение
iгт = ωтур / ωнас
ωтур – угловая скорость турбинного
колесаωнас – угловая скорость насосного колеса
скольжение (в %)
sгт = 100∙(ωнас - ωтур) / ωнас =100 ∙(1 - iгт)
Кинематические параметры:
Слайд 6Основные параметры гидродинамической передачи:
коэффициент трансформации
Kгт = Mтур / Mнас
Mтур
– крутящий момент на турбинном колесе
Mнас – крутящий момент на
насосном колесеλнас и λтур – коэффициенты пропорциональности крутящих моментов
Силовые (преобразующие) параметры:
Слайд 7Основные параметры гидродинамической передачи:
коэффициент полезного действия
ηгт(iгт), Kгт(iгт), λнас(iгт)
Энергетические параметры:
Безразмерные характеристики:
Слайд 8К гидродинамическим передачам относятся гидромуфта и гидротрансформатор, которые отличаются конструктивно
и имеют различные характеристики.
Принцип работы гидромуфты
Слайд 101 – входной вал; 2 – выходной вал; 3 –
корпус;
Н – насосное колесо; Т – турбинное колесо; Р
– реактор;М – муфта свободного хода; Ф – фрикцион
Схемы гидротрансформатора
Слайд 11У гидротрансформатора
Kгт ≥ 1 (при Kгт = 1 переходит
на режим гидромуфты);
Лучше работать при ηгт > 0,8
Слайд 12Имеются следующие характерные точки:
1. В стоповом режиме (iгт = 0)
Kгт
max = 2…2,5 – у легковых КМ; Kгт max = 2,2…4
– у грузовых КМ.2. Передаточное отношение iгт муф = 0,84…0,87 характеризует переход на режим гидромуфты.
3. Максимальное значение КПД ηгт max = 0,88…0,92 находится в диапазоне iгтη = 0,7…0,8.
4. Ограничение эксплуатационного режима диапазоном iгтη = 0,4…0,6 при КПД ηгт э ≈ 0,8.
5. Максимальное значение коэф. пропорциональности момента iгтλ
Слайд 13Диапазон 0 ≤ iгт ≤ iгт э используется при трогании
КМ с места, при большом сопротивлении движению и низком коэффициенте
сцепления.Зависимость λнас(iгт) характеризует прозрачность гидродинамической передачи – способность передавать двигателю изменение нагрузки на валу турбины.
Слайд 14Прозрачность гидродинамической передачи оценивают коэффициентом прозрачности:
Пгт = λнас max /
λнас муф.
Слайд 15Рассматривают три вида прозрачности:
при увеличении iгт значения λнас уменьшаются –
прямая;
при увеличении iгт значения λнас увеличиваются – обратная;
λнас имеет максимум
в диапазоне 0 ≤ iгт ≤ iгт муф – смешанная.
Слайд 16В зависимости от значения коэффициента прозрачности гидродинамические передачи подразделяют на:
Пгт
= 1…1,2 – непрозрачная
(двигатель не реагирует на изменение сопротивления
движению КМ); Пгт = 1,2…1,5 – малопрозрачная;
Пгт > 1,5 – прозрачная.
Слайд 17Это объясняется тем, что эти передачи, в отличие от механической,
не обеспечивают жесткой, однозначной связи вала двигателя с ведущими колесами,
при которой величина крутящего момента ведущих колес определяется произведением крутящего момента двигателя на передаточное число трансмиссии (без учета потерь), а угловая скорость колес – делением угловой скорости вала двигателя на то же передаточное число.При наличии в КМ гидродинамической передачи невозможно рассчитывать тяговую характеристику так, как при механической трансмиссии.
Слайд 18Совместная работа двигателя и гидротрансформатора определяется нагрузочной характеристикой двигателя с
гидродинамической передачей.
Слайд 19Согласующая передача (СП) обеспечивает согласование оборотов двигателя и рабочих оборотов
насосного колеса.
Слайд 20Для совместной работы необходимо, чтобы момент, поступающий к валу насосного
колеса воспринимался гидравлическим моментом на его лопатках
при
Слайд 21Пересечения кривых Mсп(nсп) и Mнас(nнас) при nсп = nнас определяют
точку совместной работы двигателя с гидродинамической передачей.
Слайд 22Для непрозрачных передач (λнас ≈ const) зависимость Mнас(nнас) и график
совместной работы характеризуется узким пучком парабол, который обычно заменяют одной
параболой.Совместная работа при неизменной подаче топлива возможна только при одной частоте, неизменной при изменении iгт. Этой частоте соответствует определенное значение момента Mнас.
Слайд 23Если выбрать кривую, проходящую через точку A (сплошная линия), то
можно использовать полную мощность двигателя, но она проходит далеко от
зоны минимального удельного расхода топлива, поэтому частичные режимы работы двигателя будут неэкономичными.
Слайд 24Если выбрать кривую, проходящую через точку B (штрихпунктирная линия), обеспечивающую
работу двигателя при минимальном удельном расходе двигателя, то исключается возможность
использования полной мощности двигателя и снижаются тягово-скоростные свойства КМ.Следовательно, непрозрачный гидротрансформатор не позволяет в полной мере реализовать возможности двигателя и его применение нецелесообразно.
Слайд 25Для прозрачных передач зависимости Mнас(nнас) и графики совместной работы характеризуются
пучком парабол, ширина которых тем больше, чем больше коэффициент прозрачности
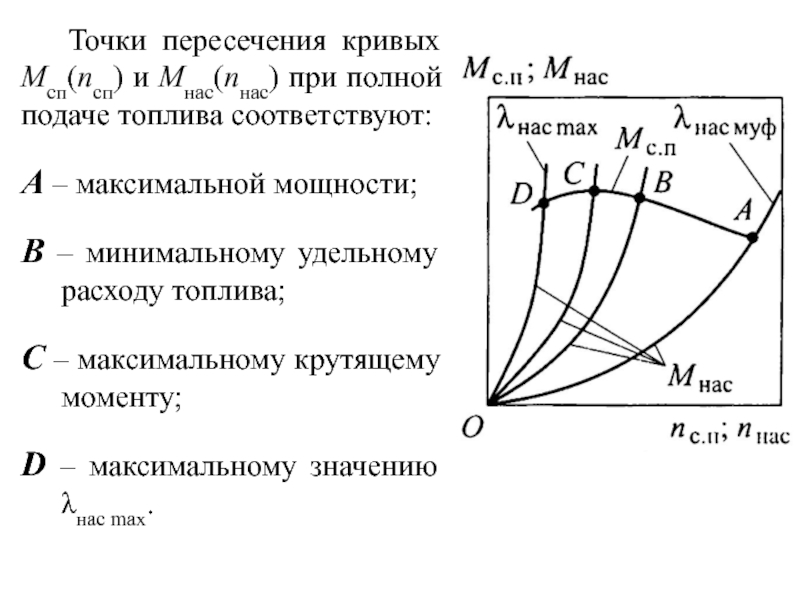
Пгт. Следовательно, он имеет множество нагрузочных характеристик
Слайд 26Точки пересечения кривых Mсп(nсп) и Mнас(nнас) при полной подаче топлива
соответствуют:
A – максимальной мощности;
B – минимальному удельному расходу топлива;
C – максимальному крутящему моменту;
D – максимальному значению λнас max.
Слайд 27Нагрузочная кривая, получаемая при λнас max, должна обязательно пересекаться с
кривой Mсп(nсп) при полной подаче топлива, что обеспечивает устойчивую работу
двигателя в любых эксплуатационных условиях, исключает его перегрузку и остановку.
Слайд 28Для определения динамической характеристики Dф(mм; vxм; uтр) КМ с гидродинамической
передачей необходимо определить параметры на валу входа в механическую часть
трансмиссии.Динамическая характеристика
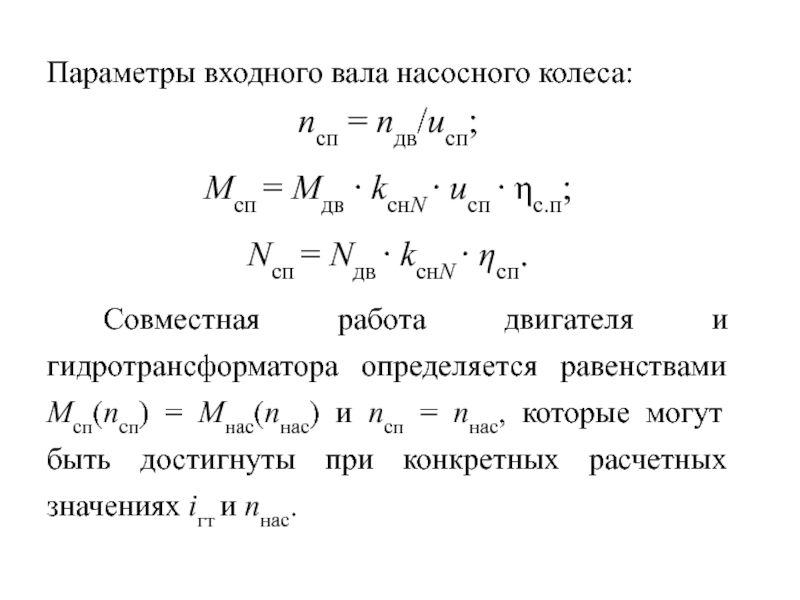
Слайд 29Параметры входного вала насосного колеса:
nсп = nдв/uсп;
Mсп =
Mдв ∙ kснN ∙ uсп ∙ ηс.п;
Nсп = Nдв
∙ kснN ∙ ηсп. Совместная работа двигателя и гидротрансформатора определяется равенствами Mсп(nсп) = Mнас(nнас) и nсп = nнас, которые могут быть достигнуты при конкретных расчетных значениях iгт и nнас.
Слайд 30Определяются параметры на выходном валу турбинного колеса, связанном жестко с
входным валом механической части трансмиссии:
Mтур = Kгт ∙ Mсп
nтур
= iгт ∙ nспNтур = Nнас ∙ ηгт ≈ Nсп ∙ Kгт ∙ iгт
Слайд 31Дальнейший расчет аналогичен рассмотренному ранее расчету для случая механической трансмиссии:
Pкм = Mтур ∙ uтр ∙ ηтр / rк0
vмx
= 0,105 ∙ rк ∙ nтур / uтр Dф = (Pкм - Pw) / Pм
Nкм = Nтур ∙ ηтр
Слайд 32Дифференциальное уравнение прямолинейного движения КМ с гидромеханической передачей аналогично уравнению,
полученному для механической передачи
где δвр гт – коэффициент учета вращающихся
масс, учитывающий влияние моментов инерции насосного и турбинного колес на изменение кинетической энергии системы.
Слайд 33где Jспi – момент инерции i-й вращающейся массы согласующей передачи;
ui – передаточное число от i-й массы до насосного колеса.
Суммарный
момент инерции двигателя Jдв, согласующей передачи Jспi и насосного колеса с массой жидкости в его полости Jнас:
Слайд 34Суммарный инерционный момент двигателя, согласующей передачи и насосного колеса:
MJ
дв-нас = - Jдв-нас dωнас/dt
Инерционный момент турбинного колеса
MJ тур
= - Jтур dωтур/dt.После преобразований получим:
Слайд 35Для непрозрачного гидротрансформатора
dωнас / dt = 0.
У прозрачного
гидротрансформатора δвр гт переменная не только в зависимости от передаточного
числа трансмиссии uтр, но и от скорости движения в пределах одной передачи, так как отношение dωнас/dt изменяется с изменением величины ωтур.
Слайд 36Тягово-скоростные и разгонные характеристики КМ 8х8
Для обеспечения работы ГТ в
экономичном режиме при недостаточном значении Kгт необходимо использовать несколько передач
в механической части трансмиссии
