Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УГЛЫ
Содержание
- 1. УГЛЫ
- 2. ЦЕЛИ УРОКА:ВВЕСТИ ПОНЯТИЕ ЦЕНТРАЛЬНОГО И ВПИСАННОГО УГЛА;РАССМОТРЕТЬ
- 3. 1.Что называют углом?2. Классифицируйте углы по градусной
- 4. 4. Как называются углы, на рисунках?Центральный и вписанный угол
- 5. Центральным углом окружности называют угол с вершиной
- 6. Градусная мера вписанного угла равна половине градусной
- 7. Слайд 7
- 8. ТЕОРЕМАКасательная к окружности перпендикулярна к радиусу, проведенному
- 9. ЗАДАЧА 1 (СВОЙСТВО УГЛА МЕЖДУ КАСАТЕЛЬНОЙ И
- 10. Слайд 10
- 11. ТЕОРЕМАКаждая точка биссектрисы неразвернутого угла равноудалена от
- 12. Определение Серединным перпендикуляром к отрезку называется прямая,
- 13. ТЕОРЕМАВысоты треугольника (или их продолжения) пересекаются в
- 14. ОКРУЖНОСТЬ НАЗЫВАЕТСЯ ОПИСАННОЙ ОКОЛО ЧЕТЫРЁХУГОЛЬНИКА, ЕСЛИ ОНА
- 15. Скачать презентанцию
ЦЕЛИ УРОКА:ВВЕСТИ ПОНЯТИЕ ЦЕНТРАЛЬНОГО И ВПИСАННОГО УГЛА;РАССМОТРЕТЬ ЗАДАЧИ НА ПРИМЕНЕНИЕ ЭТИХ ПОНЯТИЙ;СФОРМИРОВАТЬ КОНСТРУКТИВНЫЙ НАВЫК НАХОЖДЕНИЯ УГЛА .
Слайды и текст этой презентации
Слайд 2ЦЕЛИ УРОКА:
ВВЕСТИ ПОНЯТИЕ ЦЕНТРАЛЬНОГО И ВПИСАННОГО УГЛА;
РАССМОТРЕТЬ ЗАДАЧИ НА ПРИМЕНЕНИЕ
ЭТИХ ПОНЯТИЙ;
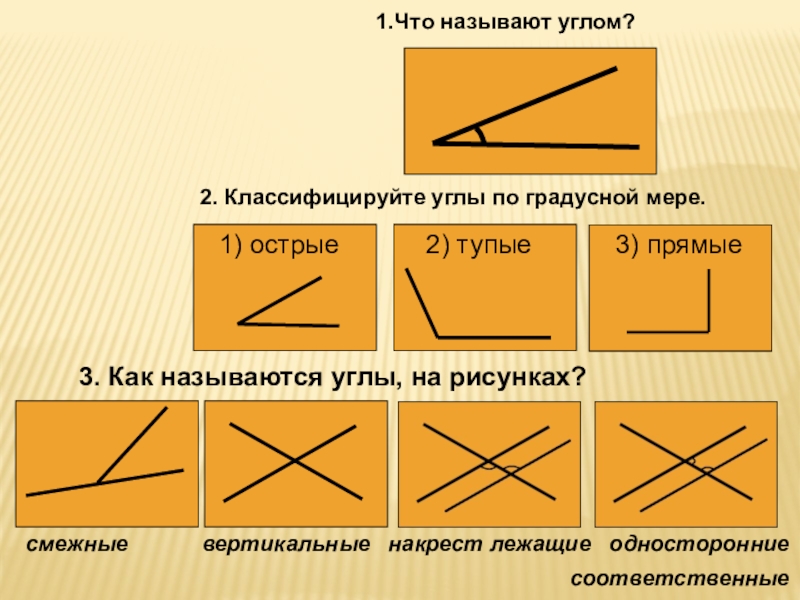
Слайд 31.Что называют углом?
2. Классифицируйте углы по градусной мере.
3. Как называются
углы, на рисунках?
смежные
вертикальные накрест лежащие односторонниесоответственные
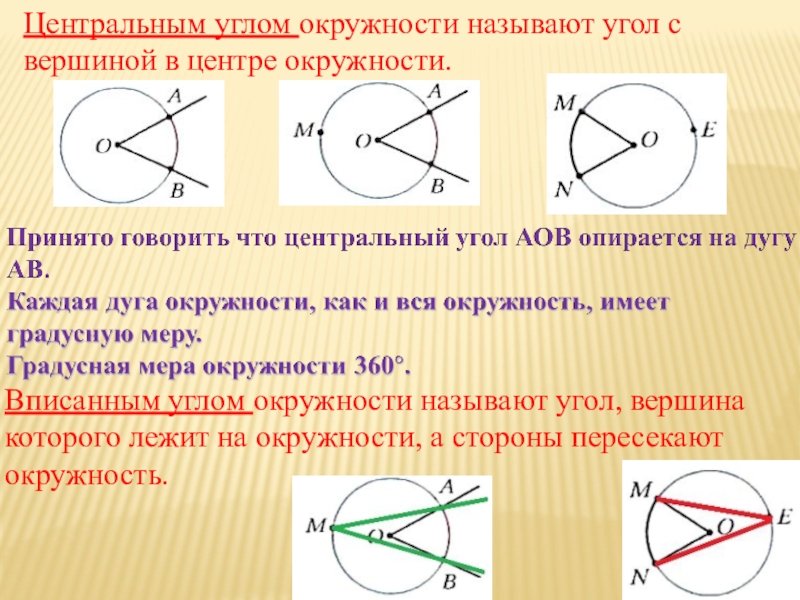
Слайд 5Центральным углом окружности называют угол с вершиной в центре окружности.
Вписанным
углом окружности называют угол, вершина которого лежит на окружности, а
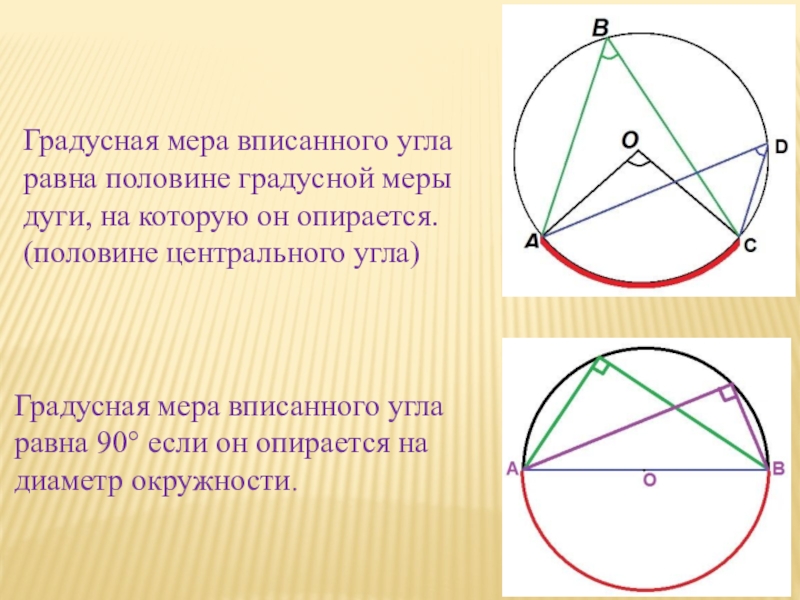
стороны пересекают окружность.
Слайд 6Градусная мера вписанного угла равна половине градусной меры дуги, на
которую он опирается.
(половине центрального угла)
Градусная мера вписанного угла равна
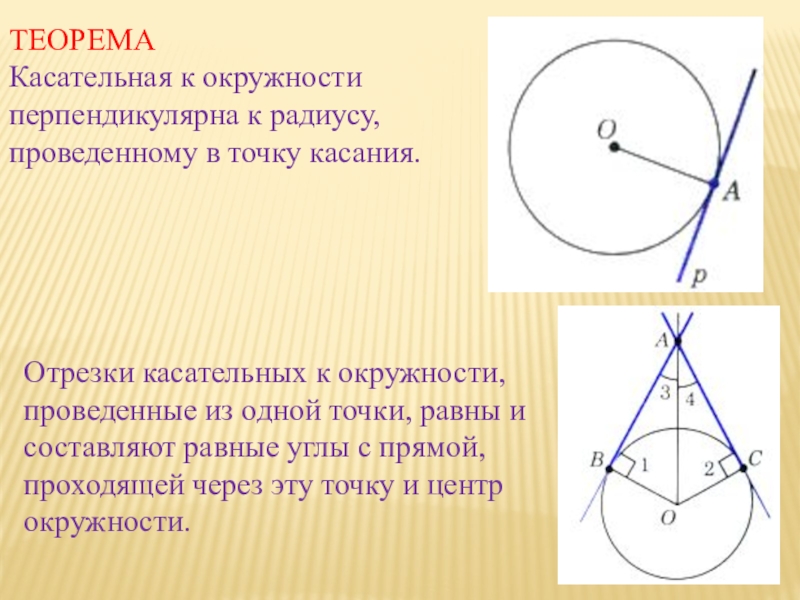
90° если он опирается на диаметр окружности. 
Слайд 8ТЕОРЕМА
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны и
составляют равные углы с прямой, проходящей через эту точку и центр окружности. 
Слайд 9ЗАДАЧА 1 (СВОЙСТВО УГЛА МЕЖДУ КАСАТЕЛЬНОЙ И ХОРДОЙ)
Отрезок АВ- хорда
окружности с центром О. Через точку А проведена касательная MN.
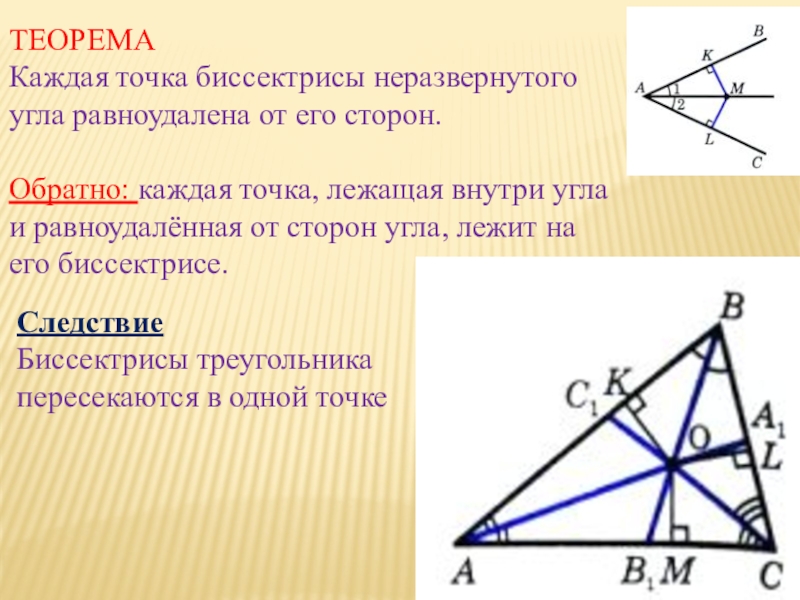
Докажите что
Слайд 11ТЕОРЕМА
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Обратно: каждая
точка, лежащая внутри угла и равноудалённая от сторон угла, лежит
на его биссектрисе.Следствие
Биссектрисы треугольника пересекаются в одной точке
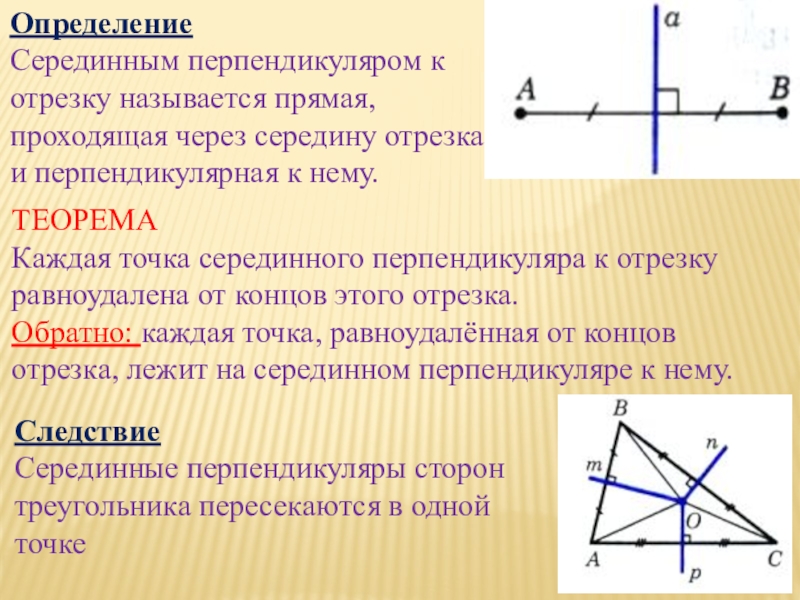
Слайд 12Определение
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину
отрезка и перпендикулярная к нему.
ТЕОРЕМА
Каждая точка серединного перпендикуляра к отрезку
равноудалена от концов этого отрезка.Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Следствие
Серединные перпендикуляры сторон треугольника пересекаются в одной точке
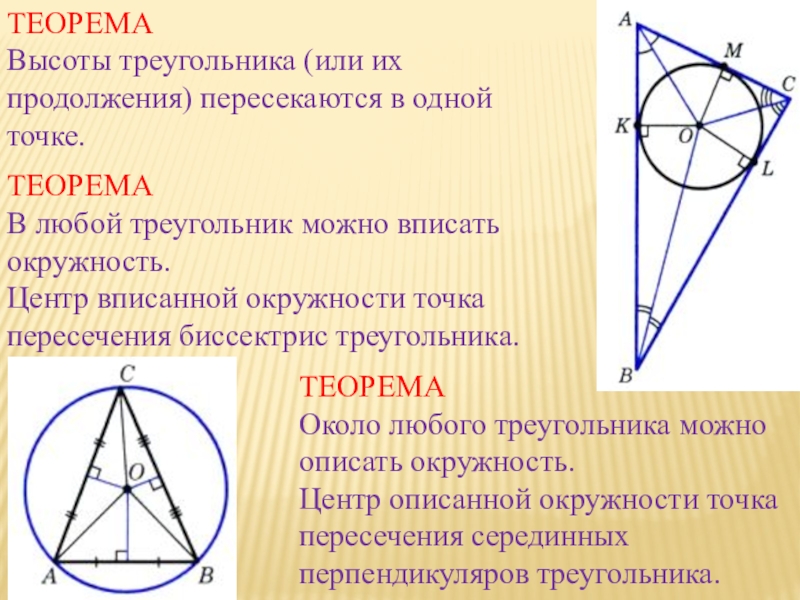
Слайд 13ТЕОРЕМА
Высоты треугольника (или их продолжения) пересекаются в одной точке.
ТЕОРЕМА
Около любого
треугольника можно описать окружность.
Центр описанной окружности точка пересечения серединных
перпендикуляров треугольника.ТЕОРЕМА
В любой треугольник можно вписать окружность.
Центр вписанной окружности точка пересечения биссектрис треугольника.
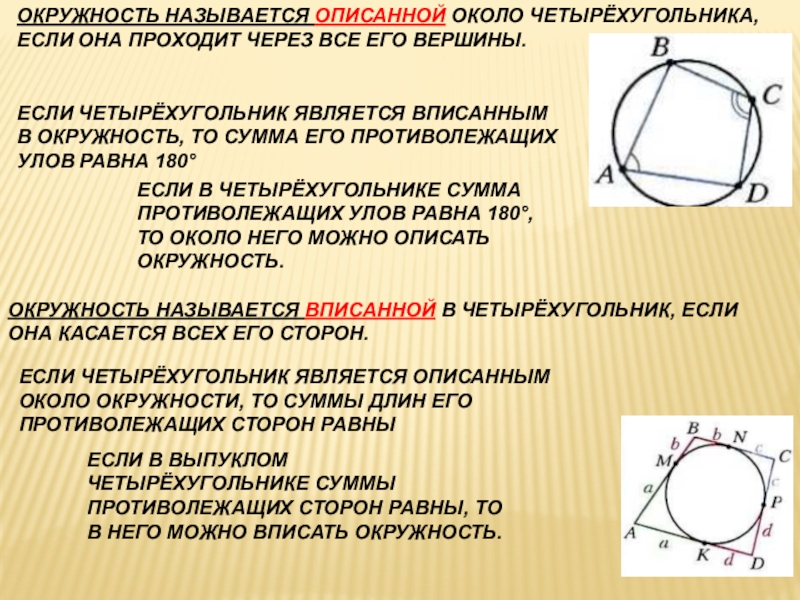
Слайд 14ОКРУЖНОСТЬ НАЗЫВАЕТСЯ ОПИСАННОЙ ОКОЛО ЧЕТЫРЁХУГОЛЬНИКА, ЕСЛИ ОНА ПРОХОДИТ ЧЕРЕЗ ВСЕ
ЕГО ВЕРШИНЫ.
ЕСЛИ ЧЕТЫРЁХУГОЛЬНИК ЯВЛЯЕТСЯ ВПИСАННЫМ В ОКРУЖНОСТЬ, ТО СУММА ЕГО
ПРОТИВОЛЕЖАЩИХ УЛОВ РАВНА 180°ЕСЛИ В ЧЕТЫРЁХУГОЛЬНИКЕ СУММА ПРОТИВОЛЕЖАЩИХ УЛОВ РАВНА 180°, ТО ОКОЛО НЕГО МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ.
ОКРУЖНОСТЬ НАЗЫВАЕТСЯ ВПИСАННОЙ В ЧЕТЫРЁХУГОЛЬНИК, ЕСЛИ ОНА КАСАЕТСЯ ВСЕХ ЕГО СТОРОН.
ЕСЛИ ЧЕТЫРЁХУГОЛЬНИК ЯВЛЯЕТСЯ ОПИСАННЫМ ОКОЛО ОКРУЖНОСТИ, ТО СУММЫ ДЛИН ЕГО ПРОТИВОЛЕЖАЩИХ СТОРОН РАВНЫ
ЕСЛИ В ВЫПУКЛОМ ЧЕТЫРЁХУГОЛЬНИКЕ СУММЫ ПРОТИВОЛЕЖАЩИХ СТОРОН РАВНЫ, ТО В НЕГО МОЖНО ВПИСАТЬ ОКРУЖНОСТЬ.
