Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УрФУ Кафедра Технологии Сварочного Производства Квалиметрия Шкала
Содержание
- 1. УрФУ Кафедра Технологии Сварочного Производства Квалиметрия Шкала
- 2. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиСогласованность ранжировок «Обобщенная»
- 3. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировки«Школа» - часть
- 4. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиСогласованность ранжировок Как
- 5. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиСогласованность ранжировок Характеристики
- 6. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиСогласованность ранжировок Характеристики
- 7. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиСогласованность ранжировок Характеристики
- 8. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиФормальные характеристики взаимосвязи
- 9. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиФормальные характеристики взаимосвязи
- 10. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиФормальные характеристики взаимосвязи
- 11. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировокВыбор
- 12. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«По
- 13. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Наиболее
- 14. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 15. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 16. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 17. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 18. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 19. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 20. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиАлгоритмы обобщения ранжировок«Алгоритм
- 21. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиМатрица предпочтений В
- 22. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиМатрица предпочтений Вернемся
- 23. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияПри проверке по первой
- 24. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиПоиск медиан Кемени
- 25. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаРанжировкиСредняя ранжировка по
- 26. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияШкала порядкаСвязанные и нормализованные
- 27. УрФУКафедра Технологии Сварочного ПроизводстваКвалиметрияМетоды измерения качества Для
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Вид (экспертной) оценки, при которой объекты
Слайд 2УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Согласованность ранжировок
«Обобщенная» ранжировка некоторым «наилучшим»
образом представляет обобщенное суждение экспертов в случае достаточной согласованности их
индивидуальных ранжировок между собойПонятие «наилучшей» согласованности различно для разных задач. Выбор статистических характеристик среднего, согласованности, как и всех операций статобработки, также зависит от содержания решаемой квалиметрической задачи
Вне зависимости от вида задачи в группе индивидуальных ранжировок (как и в экспертных оценках других видов) выделяют рассогласованность по типу «школы» и по типу «еретиков»
Слайд 3УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
«Школа» - часть экспертов из, чьи
индивидуальные ранжировки достаточно согласованы между собой, но отличаются от обобщенной
ранжировки бόльшей части экспертов, чьи индивидуальные ранжировки также хорошо согласованы между собой«Еретик» - отдельный эксперт, чья ранжировка не согласована (по принятому критерию) с обобщенной ранжировкой согласованной экспертной группы
Слайд 4УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Согласованность ранжировок
Как правило, получение обобщенной
ранжировки возможно только для индивидуальных ранжировок, принадлежащих к одной согласованной
группеЛюбые две ранжировки, различающиеся взаимным расположением хотя бы двух объектов, можно считать согласованными в одних задачах и рассогласованными в других
Ранжировки, различающиеся расположением объектов A и B
A>B>C>D
B>A>C>D
являются согласованными, если задача состоит в выборе 2-х лидирующих объектов из 4-х (например, в задаче определения приоритета). Тогда обобщенная ранжировка будет иметь вид:
(A~B)>C>D
Если же задача состоит в выборе одного лидирующего объекта, то эти же ранжировки нельзя считать согласованными
Слайд 5УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Согласованность ранжировок
Характеристики положения объектов, входящих
в ранжировки
1) частость присвоения объекту A ранга 1 (частость
максимально возможных оценок для объекта А): 2) частость присвоения объекту А ранга не более R:
3) модальный ранг объекта RМо — ранг, присвоенный объекту наибольшим числом экспертов
Слайд 6УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Согласованность ранжировок
Характеристики положения и характеристики
неопределенности положения объектов, входящих в ранжировки
4). Для каждой пары
объектов А и В может быть определена частость предпочтения объекта А объекту В и наоборот: Р(А>В) или Р(В>А). Меньшую из них используют для характеристики неопределенности взаимного расположения объектов. Максимальная неопределенность расположения объекта будет равна 0,5Отношение чисел экспертов, предложивших предпочтения А>В и В>А, то есть n(А>В)/n(В>А), представляет собой удобную форму записи промежуточных результатов при решении практических задач
Слайд 7УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Согласованность ранжировок
Характеристики неопределенности положения объектов,
входящих в ранжировки
Показатели неопределенности положения объекта по совокупности экспертных
ранжировок:1). концентрация расположения оценок объекта возле модального ранга: указывает долю экспертов, присвоивших объекту модальный ранг и два ранга смежных с ним
2). размах (диапазон) отклонений объекта: указывают максимальный и минимальный ранги, присвоенные объекту: Rmin, Rmax
Слайд 8УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Формальные характеристики взаимосвязи (близости) ранжировок
Близость двух
ранжировок может быть оценена числом любых фиксированных «элементарных» операций, переводящих
одну из них в другую«Инверсия» — перемена мест пары рядом стоящих объектов
Максимальное расстояние между двумя ранжировками, каждая из которых содержит n объектов
S- - число инверсий, S+ - число неинвертированных объектов
Коэффициент ранговой корреляции Кендэла
+1 - значительная близость суждений экспертов
0 - отсутствие связи между суждениями
-1 - противоположность суждений
Ранжировка B>C>A>D>E может быть приведена к ранжировке A>B>С>D>E
переменой мест объектов
1). А и С
2). А и В
Расстояние между ними — две инверсии
Слайд 9УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Формальные характеристики взаимосвязи (близости) ранжировок
Для определения
степени согласованности мнений двух экспертов - коэффициент ранговой корреляции Спирмена
где хj и уj - ранги, установленные двумя экспертами; n — число факторов
+1 - значительная близость суждений экспертов
0 - отсутствие связи между суждениями
-1 - противоположность суждений
Слайд 10УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Формальные характеристики взаимосвязи (близости) ранжировок
Для характеристики
согласованности группы индивидуальных ранжировок наиболее часто применяют коэффициент конкордации Кендэла
где:
Si
— сумма рангов, полученных данным объектом во всех ранжировках;S —средняя сумма рангов, полученная одним объектом;
т — число экспертов;
п — число ранжируемых объектов
0 - полная несогласованность
1 - полная согласованность
Согласованность группы считают высокой при W > 0,8
Слайд 11УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
Выбор алгоритма получения обобщенной
ранжировки, как и выбор других операций статистической обработки ранжировок, зависит
от сущности решаемой задачи По возрастанию суммы рангов
Наиболее вероятная ранжировка
Алгоритм выделения лидера (аутсайдера)
Алгоритм перехода границы
Алгоритм выбора наиболее согласованно проранжированных объектов
Слайд 12УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«По возрастанию суммы рангов»
Ранги, данные каждым экспертом объекту, суммируются. Выстраивается ряд по полученным
суммам. Производится присвоение номеров (итоговых рангов) согласно порядка в полученном ряду Проблема: возможно получение одинаковых сумм для некоторых или для всех объектов
Для ранжировок
А>В>С
В>C>A
C>A>B
сумма рангов для каждого равна 6
Слайд 13УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Наиболее вероятная ранжировка»
Для
ряда, состоящего из объектов: A, B, C ..., частости предпочтений
Р(А>В) могут служить оценками вероятностей предпочтенийКаждую пару объектов можно расположить в порядке, соответствующем большей из вероятностей предпочтения: А>В; А>С; В>С ..., и таким образом, может быть построен ряд наиболее вероятного предпочтения: А>В>С...
Применение алгоритма наиболее вероятной ранжировки в некоторых случаях невозможно. Для ранжировок трех объектов:
А>В>С
В>C>A
C>A>B
при расположении объектов по наибольшей вероятности получаем:
А>В(2 : 1); В>С(2 : 1); С>А(2 : 1).
Слайд 14УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм выделения лидера»
После
выделения лидирующего объекта его исключают из всех ранжировок и правило
выделения применяют к оставшимся объектамМягкое правило выделения лидера. Объект А считают лидером группы, если он занимает первое место в большем числе ранжировок, чем любой другой объект. Если два объекта (А и В) занимают первое место в одинаковом числе ранжировок, то лидером считают тот из них, который занимает большее число вторых мест и т.д.
Жесткое правило выделения лидера. Объект А является лидером группы, если он занимает первое место не менее, чем в 0,9 всех ранжировок.
Если применение такого жесткого правила не позволяет выделить очередной лидирующий объект, то можно:
установить отношение безразличия между претендующим на лидерство объектом В и следующим за ним С и, рассматривая их совместно как единый объект (В - C, проверить его лидерство по отношению к следующим объектам
изменить алгоритм обобщения
перейти к содержательной операции обобщения с привлечением экспертов
Слайд 15УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм перехода границы»
Если
смысл обобщения состоит в выделении только группы объектов, занявших первые
k мест в обобщенной ранжировке, то важен именно вопрос, по какую сторону установленной границы расположен тот или иной ранжируемый объектАлгоритм перехода границы состоит в том, что k-1 объектов выделяют по мягкому правилу выделения лидера. Последний же, k-й объект, выделяют по достаточно жесткому правилу. Это позволяет достигнуть необходимой уверенности в рациональном отборе каждого из k первых объектов по сравнению с каждым из последующих. Если же отобрать k-й объект по жесткому правилу не удается, то его исключают из ранжировок и по жесткому правилу проверяют выбор (k-1)-гo объекта и так далее, до тех пор, пока некоторый j-й объект (j
Слайд 16УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм перехода границы»
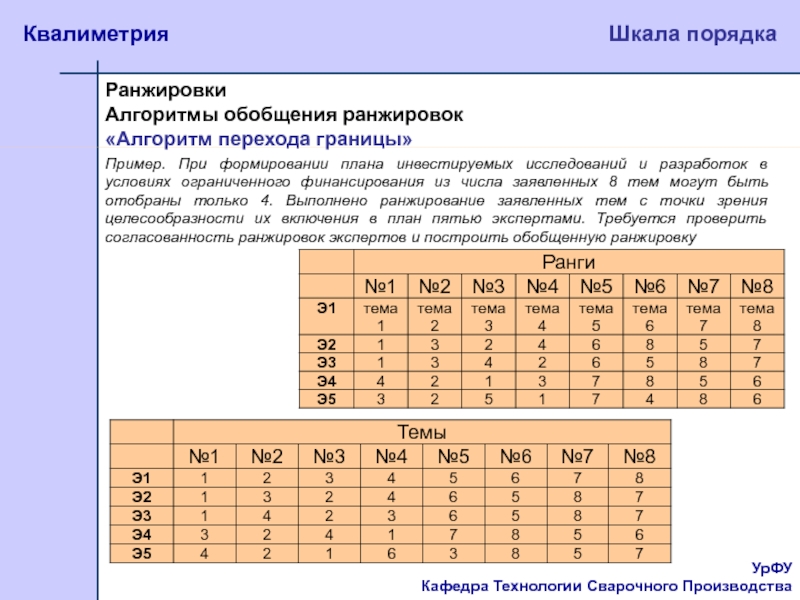
Пример.
При формировании плана инвестируемых исследований и разработок в условиях ограниченного
финансирования из числа заявленных 8 тем могут быть отобраны только 4. Выполнено ранжирование заявленных тем с точки зрения целесообразности их включения в план пятью экспертами. Требуется проверить согласованность ранжировок экспертов и построить обобщенную ранжировкуСлайд 17УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм перехода границы»
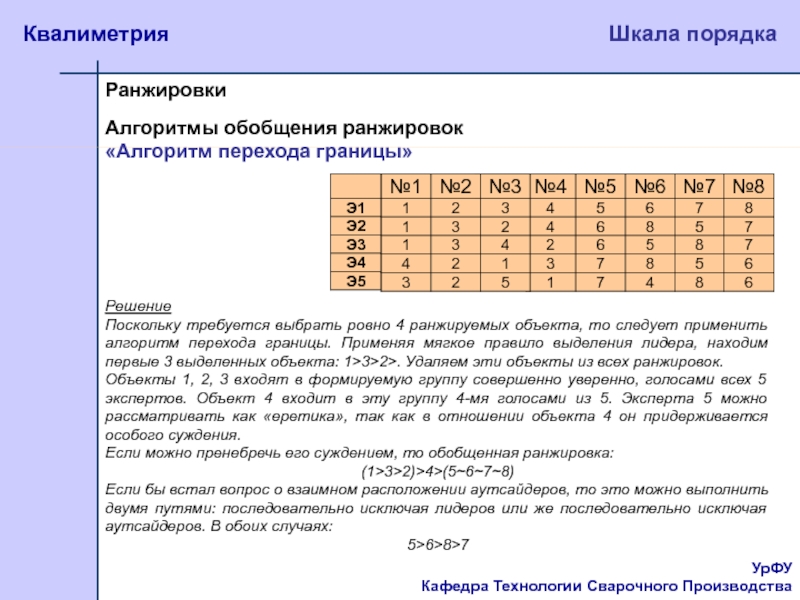
Решение
Поскольку
требуется выбрать ровно 4 ранжируемых объекта, то следует применить алгоритм
перехода границы. Применяя мягкое правило выделения лидера, находим первые 3 выделенных объекта: 1>3>2>. Удаляем эти объекты из всех ранжировок.Объекты 1, 2, 3 входят в формируемую группу совершенно уверенно, голосами всех 5 экспертов. Объект 4 входит в эту группу 4-мя голосами из 5. Эксперта 5 можно рассматривать как «еретика», так как в отношении объекта 4 он придерживается особого суждения.
Если можно пренебречь его суждением, то обобщенная ранжировка:
(1>3>2)>4>(5~6~7~8)
Если бы встал вопрос о взаимном расположении аутсайдеров, то это можно выполнить двумя путями: последовательно исключая лидеров или же последовательно исключая аутсайдеров. В обоих случаях:
5>6>8>7
Слайд 18УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм выбора наиболее согласованно
проранжированных объектов»
Иногда обобщенную ранжировку нужно составить из объектов, одинаково
расположенных друг относительно друга всеми экспертами. В ранжировкахA>B>C>D
D>B>C>A
стабильно только предпочтение В>С. Все остальные предпочтения в ранжировках различны. Следовательно и обобщенная ранжировка будет иметь вид В>С.
Для выявления наиболее согласованно проранжированных объектов можно применить матрицу предпочтений. В ячейках матрицы приводят частоты прямого и обратного предпочтений экспертами объектов. Далее выбирают в первой строке ячейку с абсолютным предпочтением (т.е. все эксперты придерживаются одинакового мнения). Пусть это будет ячейка с объектами А и В. Тогда, рассматривая столбец и строку, соответствующие объекту B, вновь находят ячейку с абсолютным предпочтением для объектов В и С и т.д. до исчерпания всех объектов. При этом получают одну из возможных обобщенных ранжировок
Слайд 19УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм выбора наиболее согласованно
проранжированных объектов»
Пример. При оценивании эстетической составляющей качества объектов и
в некоторых других случаях используют так называемый «базисный» (или «ценностный») ряд, составленный из 4-6 лучших в эстетическом отношении объектов данного назначения (автомашины, станки определенного типа, изделия бытовой техники и др.). Для составления базисного ряда из некоторого числа (10-15) таких объектов выбирают те, которые всеми экспертами расположены по эстетическому восприятию одинаково. Таким образом, из представленных экспертами ранжировок т объектов требуется выбрать n < т объектов, проранжированных всеми экспертами одинаково.
Слайд 20УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
Алгоритмы обобщения ранжировок
«Алгоритм выбора наиболее согласованно
проранжированных объектов»
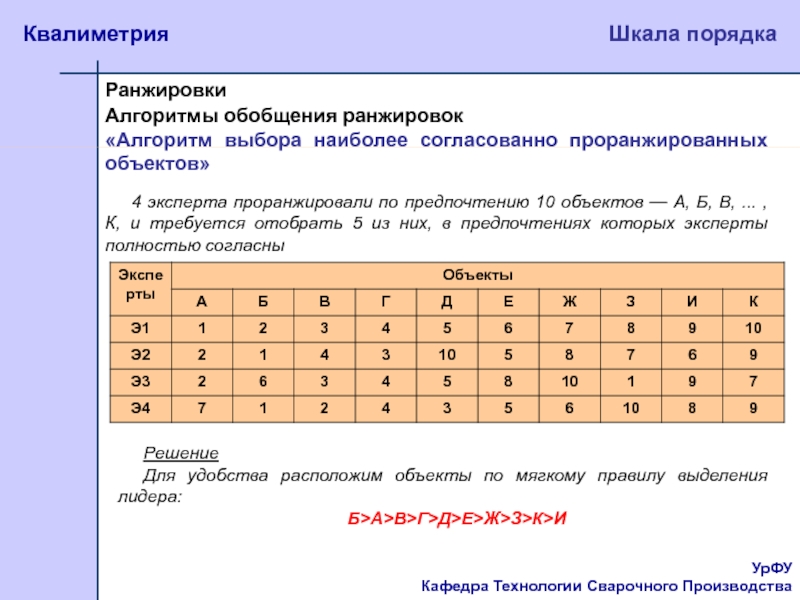
4 эксперта проранжировали по предпочтению 10 объектов —
А, Б, В, ... , К, и требуется отобрать 5 из них, в предпочтениях которых эксперты полностью согласныРешение
Для удобства расположим объекты по мягкому правилу выделения лидера:
Б>А>В>Г>Д>Е>Ж>З>К>И
Слайд 21УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
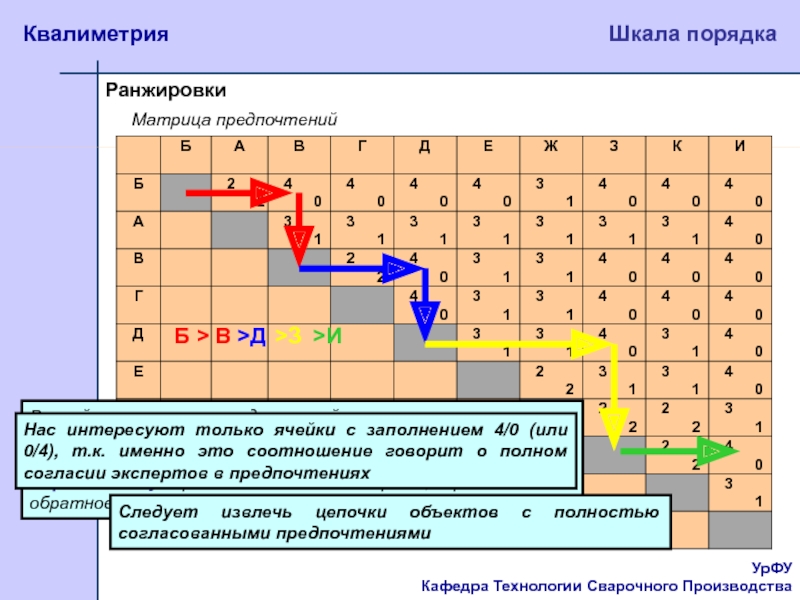
Матрица предпочтений
В ячейках матрицы предпочтений
слева вверху помещено число экспертов, предложивших предпочтение X I Y,
где X — объект в строке, Y — объект в столбце.Справа внизу приведено число экспертов, предложивших обратное предпочтение
Нас интересуют только ячейки с заполнением 4/0 (или 0/4), т.к. именно это соотношение говорит о полном согласии экспертов в предпочтениях
Следует извлечь цепочки объектов с полностью согласованными предпочтениями
Б > В
>Д
>З
>И
Слайд 22УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
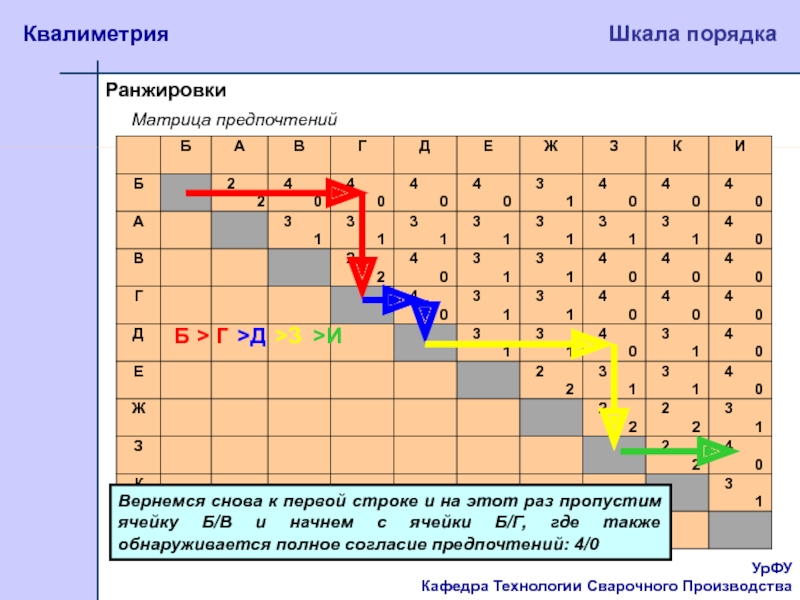
Матрица предпочтений
Вернемся снова к первой
строке и на этот раз пропустим ячейку Б/В и начнем
с ячейки Б/Г, где также обнаруживается полное согласие предпочтений: 4/0Б > Г
>Д
>З
>И
Слайд 23УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
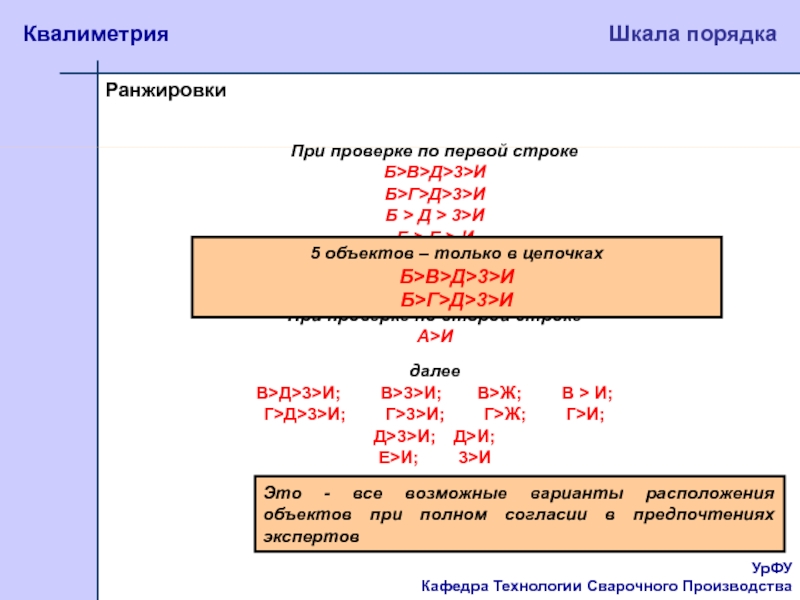
При проверке по первой строке
Б>В>Д>3>И
Б>Г>Д>3>И
Б >
Д > 3>И
Б > Е > И
Б > 3 >
ИБ > И
Шкала порядка
Ранжировки
При проверке по второй строке
А>И
далее
В>Д>3>И; В>3>И; В>Ж; В > И;
Г>Д>3>И; Г>3>И; Г>Ж; Г>И;
Д>3>И; Д>И;
Е>И; 3>И
Это - все возможные варианты расположения объектов при полном согласии в предпочтениях экспертов
5 объектов – только в цепочках
Б>В>Д>3>И
Б>Г>Д>3>И
Слайд 24УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
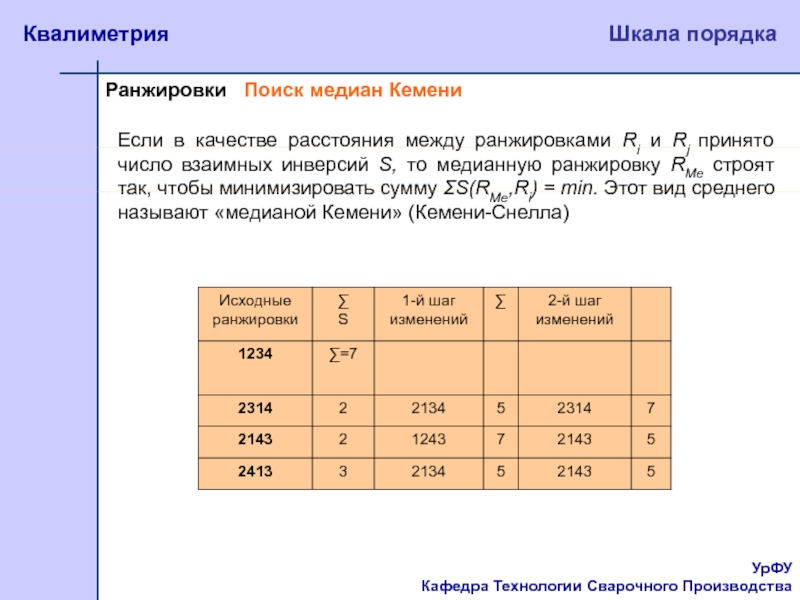
Поиск медиан Кемени
Если в качестве
расстояния между ранжировками Ri и Rj принято число взаимных инверсий
S, то медианную ранжировку RMe строят так, чтобы минимизировать сумму ΣS(RMe,Ri) = min. Этот вид среднего называют «медианой Кемени» (Кемени-Снелла)Слайд 25УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Ранжировки
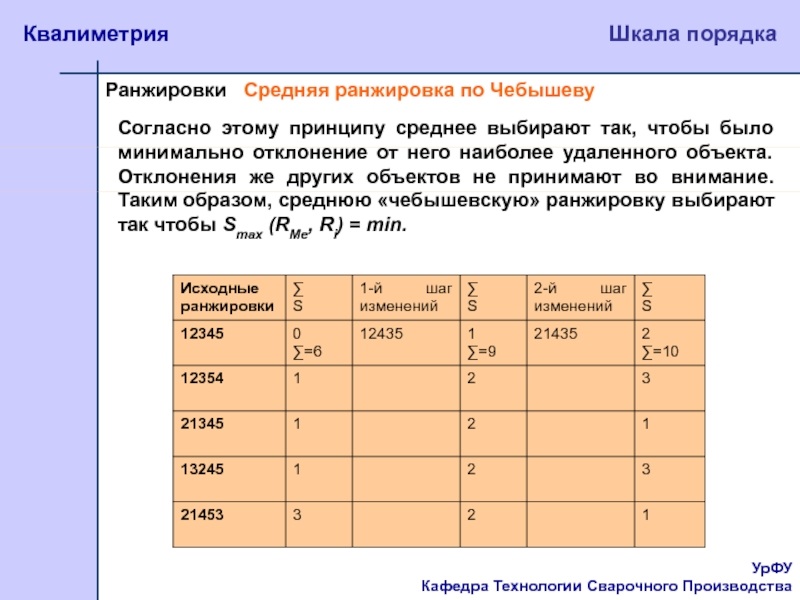
Средняя ранжировка по Чебышеву
Согласно этому
принципу среднее выбирают так, чтобы было минимально отклонение от него
наиболее удаленного объекта. Отклонения же других объектов не принимают во внимание. Таким образом, среднюю «чебышевскую» ранжировку выбирают так чтобы Smax (RMe, Ri) = min.Слайд 26УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Шкала порядка
Связанные и нормализованные ранги
Если эксперт присваивает
одинаковый ранг нескольким показателям (такой ранг называется связанным), то для
оценки используют ранги, равные среднему арифметическому значению мест, которые должны занимать показатели (такие ранги называют нормализованными).Слайд 27УрФУ
Кафедра Технологии Сварочного Производства
Квалиметрия
Методы измерения качества
Для решения каких задач
применяется ранговая шкала порядка? (приведите 2 или более конкретных примера)
Для
решения каких задач применяется реперная шкала порядка? (приведите 2 или более конкретных примера)Что представляет по сути абсолютное значение показателя по ранговой шкале?
Как вычислить относительное значение показателя по ранговой шкале?
Какие методы определения согласованности всех экспертов в отношении всех объектов экспертизы могут быть применены при оценке по ранговой шкале?
Какие параметры могут характеризовать центральную тенденцию по шкале порядка?
Какие параметры характеризуют рассеяние оценок по шкале порядка?
В каких случаях возможно применение критерия Хи-квадрат Пирсона? (цель, условия)
Какие виды рассогласования экспертов Вам известны?
Как использовать ранжирование для определения количественного соотношения свойств (или определения их весомости)?
Как вычислить среднее взвешенное арифметическое для объекта по шкале рангов?
Какие критерии согласованности двух экспертов в отношении всех объектов при оценке по ранговой шкале Вы знаете?
Какие методы определения согласованности всех экспертов в отношении всех объектов экспертизы могут быть применены при оценке по шкале отношений?