Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Условная оптимизация Функция Лагранжа
Содержание
- 1. Условная оптимизация Функция Лагранжа
- 2. 08/13/2019Постановка задачНайти минимум функцииПри ограничениях
- 3. 08/13/2019Понятие функции Лагранжа Вначале на простом примере
- 4. 08/13/2019Получение Условия минимумаВдоль кривой имеет место очевидное соотношение
- 5. 08/13/2019Получение Условия минимумаЗапишем условие минимума для функцииВдоль кривой y=y(x) имеем
- 6. 08/13/2019Условия минимумаλ– множитель ЛагранжаобозначимПолучаемПреобразуем
- 7. 08/13/2019Необходимые Условия минимумаТаким образом в точкеминимума f(x,y) на кривой g(x,y)=0выполняютсятри условия:
- 8. 08/13/2019введем функцию Лагранжа Для нее условия экстремума которые мы выше вывели получаются естественным образом
- 9. 08/13/2019Рассмотрим простой пример Функция ЛагранжаУсловия экстремумаРешение x=2; y=2; λ=4.
- 10. 08/13/2019анализ, вблизи точки экстремума точка экстремума функции
- 11. 08/13/2019функция Лагранжа для нескольких ограничений в виде
- 12. 08/13/2019Теорема о седловой точке Куна-ТаккераВ точке минимума
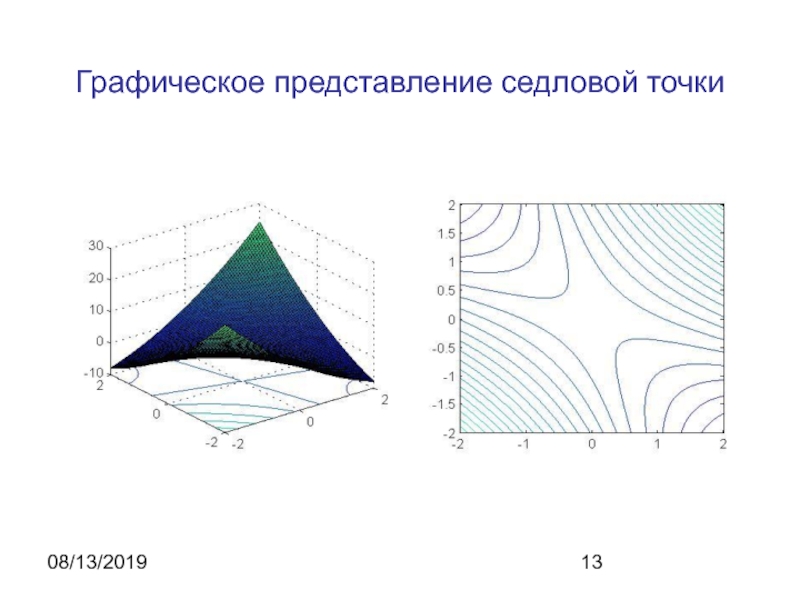
- 13. 08/13/2019Графическое представление седловой точки
- 14. 08/13/2019Условия дополнительностиЕсли пара
- 15. 08/13/2019Понятие двойственностиДопустим, что у функции Лагранжа седловая
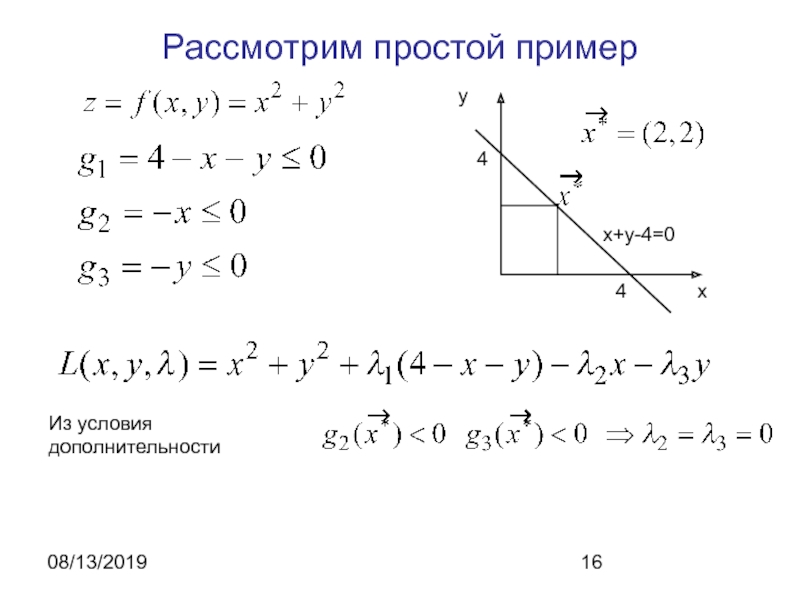
- 16. 08/13/2019Рассмотрим простой примерИз условия дополнительности
- 17. 08/13/2019Двойственная задача
- 18. 08/13/2019Задача линейного программирования
- 19. 08/13/2019Затраты: xj - количествоПример: Имеются три продукта
- 20. 08/13/2019function LinProgr1;%Задание цены продуктовc=[44; 35; 100];% Матрица
- 21. 08/13/2019Задача квадратичного программирования
- 22. 08/13/2019Задача о рискахНужно вложить некоторую сумму в
- 23. 08/13/2019Решение МатЛабfunction quadrogr1;% матрица квадратичной формы C=[102
- 24. 08/13/2019Конец
- 25. Скачать презентанцию
08/13/2019Постановка задачНайти минимум функцииПри ограничениях
Слайды и текст этой презентации
Слайд 108/13/2019
Тема 18 Методы условной оптимизации2
Понятие функции Лагранжа
Задача линейного программирования
Задача квадратичного
программирования
Слайд 308/13/2019
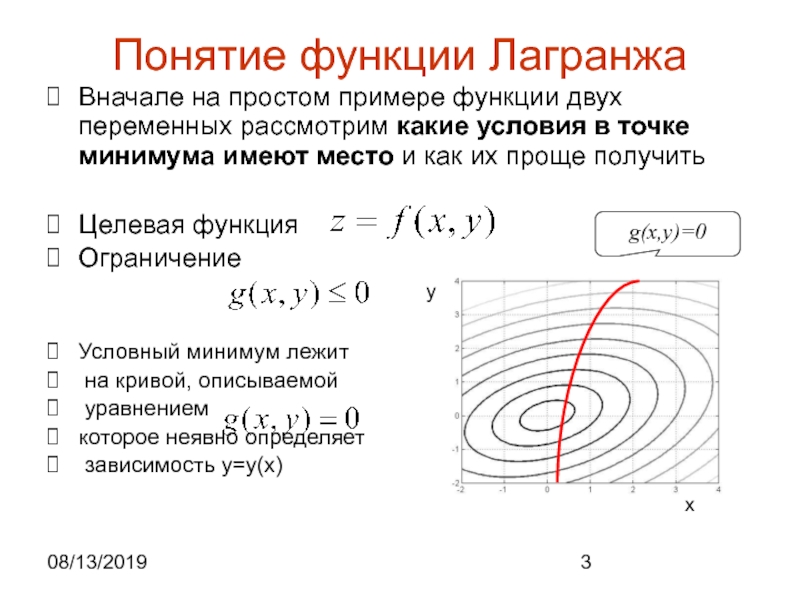
Понятие функции Лагранжа
Вначале на простом примере функции двух переменных
рассмотрим какие условия в точке минимума имеют место и как
их проще получитьЦелевая функция
Ограничение
Условный минимум лежит
на кривой, описываемой
уравнением ,
которое неявно определяет
зависимость y=y(x)
Слайд 508/13/2019
Получение Условия минимума
Запишем условие минимума для функции
Вдоль кривой y=y(x)
имеем
Слайд 708/13/2019
Необходимые Условия минимума
Таким образом в точке
минимума f(x,y)
на кривой g(x,y)=0
выполняются
три
условия:
Слайд 808/13/2019
введем функцию Лагранжа
Для нее условия экстремума которые мы выше
вывели получаются естественным образом
Слайд 1008/13/2019
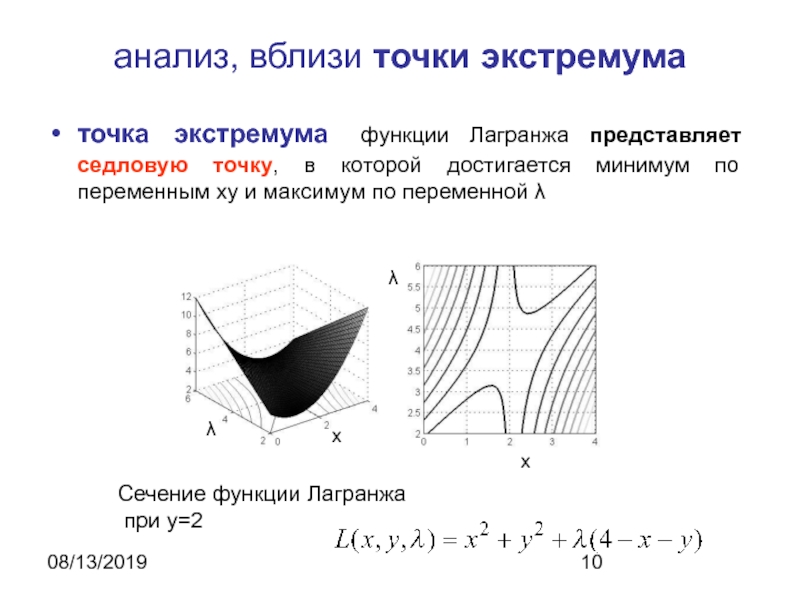
анализ, вблизи точки экстремума
точка экстремума функции Лагранжа представляет седловую
точку, в которой достигается минимум по переменным xy и максимум
по переменной λСечение функции Лагранжа
при y=2
x
λ
x
λ
Слайд 1108/13/2019
функция Лагранжа для нескольких ограничений в виде неравенств
Условие регулярности:
Существует точка
в которой
все ограничения обращаются в строгие неравенства
Слайд 1208/13/2019
Теорема о седловой точке Куна-Таккера
В точке минимума
при указанных ограничениях существует такой набор
при котором для всех
выполняетсяТочка является седловой
Слайд 1408/13/2019
Условия дополнительности
Если пара
является седловой точкой функции Лагранжа, то выполняются условия дополнительности:
Это значит, что для тех ограничений, на которых не лежит точка минимума, соответствующий множитель лагранжа равен нулю
При этом
Слайд 1508/13/2019
Понятие двойственности
Допустим, что у функции Лагранжа седловая точка существует
Положим
Аналогично
Из
свойства седловой точки
Или
Т.е можно вместо минимума находить максимум
Слайд 1908/13/2019
Затраты: xj - количество
Пример: Имеются три продукта П1,П2,П3 разной цены,
каждый из которых содержит определенное количество питательных ингридиентов И1,И2,И3,И4. Известно, что
в день требуется употребить : И1 – не менее 250, И2 ≥ 60, И3 ≥100, И4≥200. цена: П1=44, П2=35, П3=100. Требуется минимизировать затраты на приобретение ППитательность, или содержание Иi в Пj
Слайд 2008/13/2019
function LinProgr1;
%Задание цены продуктов
c=[44; 35; 100];
% Матрица ограничений
A=[4 6 15
2 2 0
5 3 4
7 3 12];A=-A;
b=[250; 60; 100; 220];
b=-b;
xm=[0; 0; 0];
% Обращение к стандартной программе
[x,p]=linprog(c,A,b,[],[],xm)
return
Результат
x =
13.2143
16.7857
6.4286
p =
1.8118e+003
Решение в МатЛаб
![08/13/2019function LinProgr1;%Задание цены продуктовc=[44; 35; 100];% Матрица ограниченийA=[4 6 15 2 2 0](/img/thumbs/16be1757ddf6af62eb2a593b8211f3e4-800x.jpg "Условная оптимизация Функция Лагранжа 08/13/2019function LinProgr1;%Задание цены продуктовc=[44; 35; 100];% Матрица ограниченийA=[4 6 15")
Слайд 2208/13/2019
Задача о рисках
Нужно вложить некоторую сумму в различные предприятия А1,А2,А3,А4
с целью получить желаемую доходность с минимальным риском.
Доли вкладов :
x1+x2+x3+x4=1; xi≥0Доходности Аi: y1 y2 y3 y4 и матрица ковариации V
Тогда доходность и риски вычисляются по формулам:
Задача:
Слайд 2308/13/2019
Решение МатЛаб
function quadrogr1;
% матрица квадратичной формы
C=[102 27 -52 66
27 148 42 -66
-52 42 246 57
66 -66 57 272];% матрицы ограничений
Ae=[11 13 16 17.5;
1 1 1 1 ];
be=[15; 1];
xm=[0; 0; 0];
% Обращение к стандартной пр-ме
[x,p]=quadprog(C,[],[],[],Ae,be,xm)
return
Результат:
Optimization terminated.
x =
0.0413
0.4511
0.1341
0.3734
p =
31.8349
