Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Установочная лекция №5
Содержание
- 1. Установочная лекция №5
- 2. План работы1. Окончание разбора темы «Структурные средние»2.
- 3. Тема 6 – Средние величины (окончание)Основные вопросы:Расчет
- 4. Давайте вспомним, что К основным структурным средним
- 5. Мо и Ме в интервальном ряду
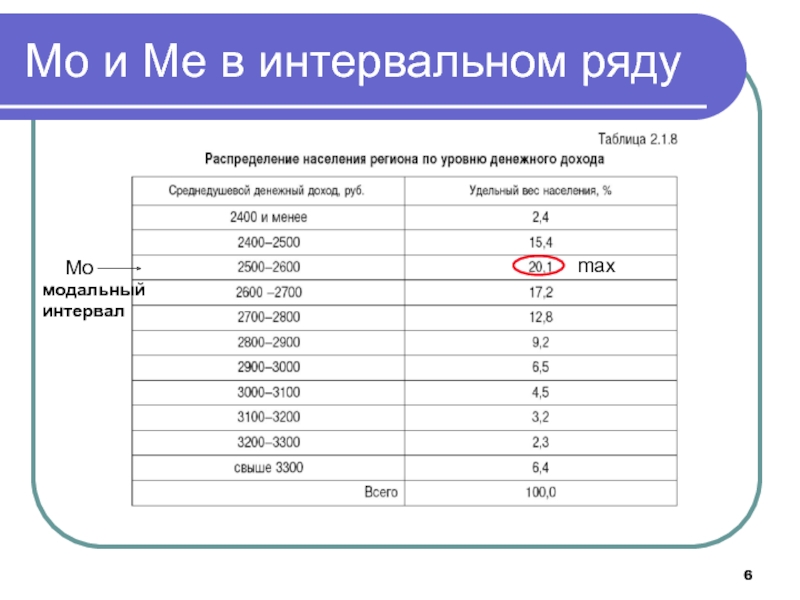
- 6. maxMo модальныйинтервалМо и Ме в интервальном ряду
- 7. Мо и Ме в интервальном ряду
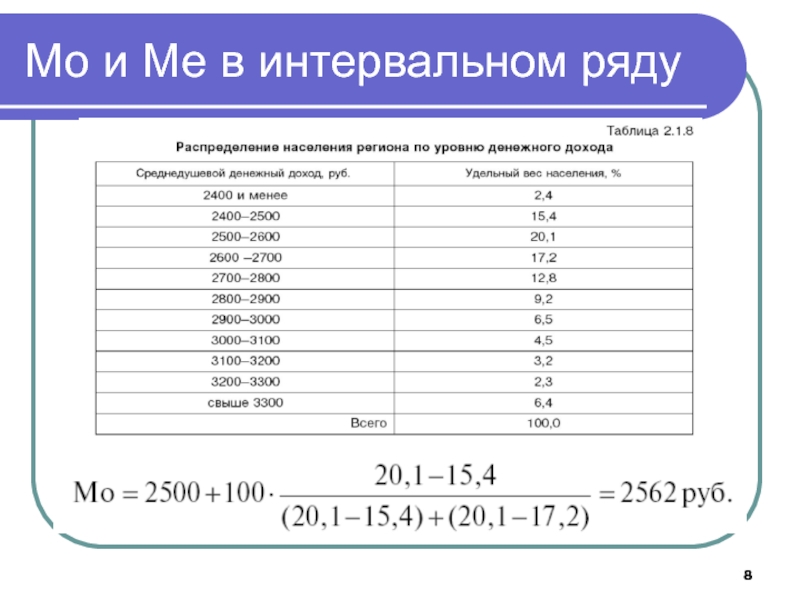
- 8. Мо и Ме в интервальном ряду
- 9. Мо и Ме в интервальном ряду
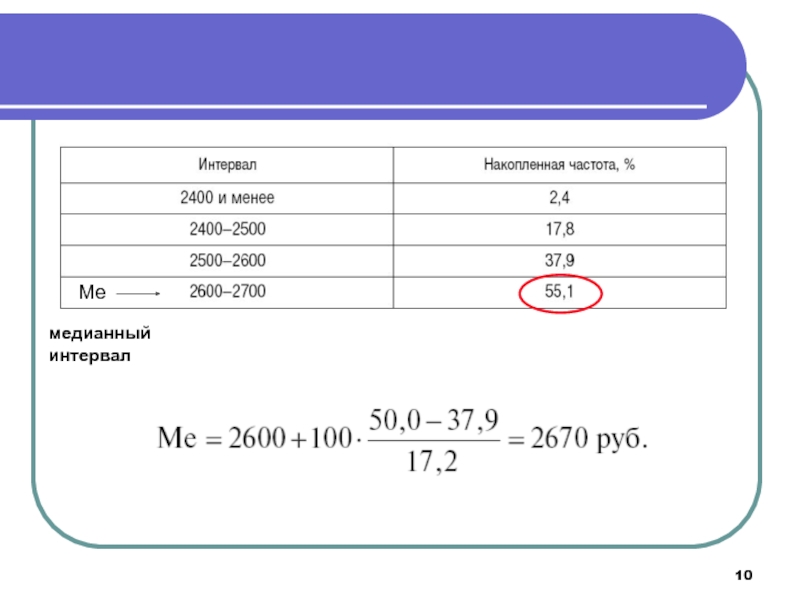
- 10. Ме медианныйинтервал
- 11. Слайд 11
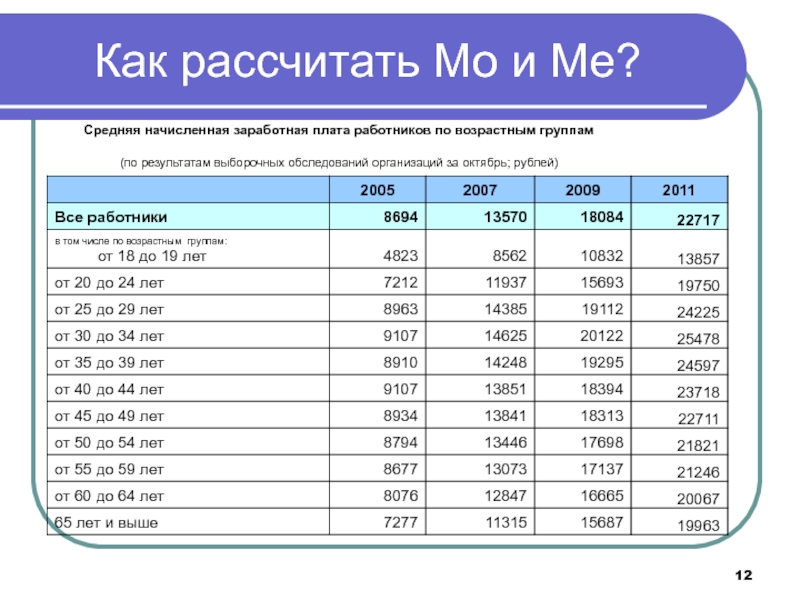
- 12. Как рассчитать Мо и Ме?
- 13. Как рассчитать Мо и Ме?Ответ: найти Мо
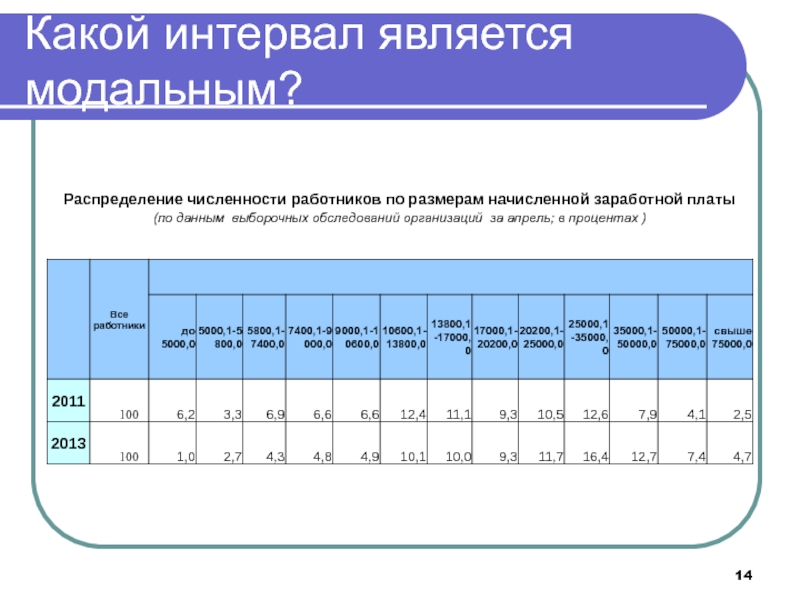
- 14. Какой интервал является модальным?
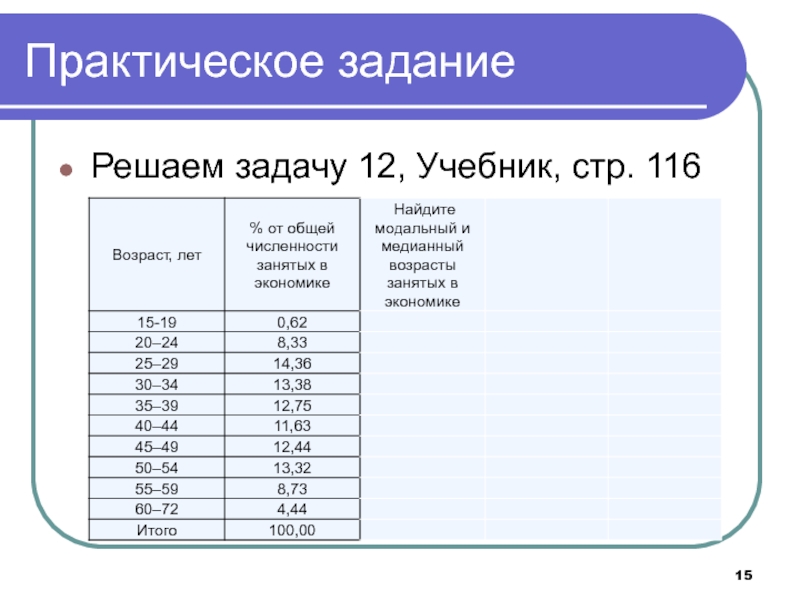
- 15. Практическое заданиеРешаем задачу 12, Учебник, стр. 116
- 16. Тема 7: Показатели вариацииПланРоль показателей вариации в
- 17. В каком случае правомерно оценивать вариацию?Вариация от лат. variatio — изменение, различие.
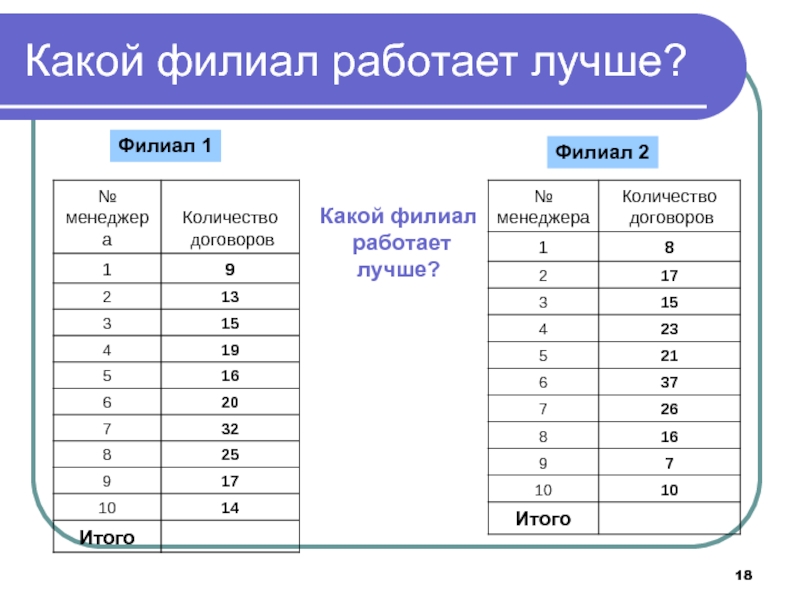
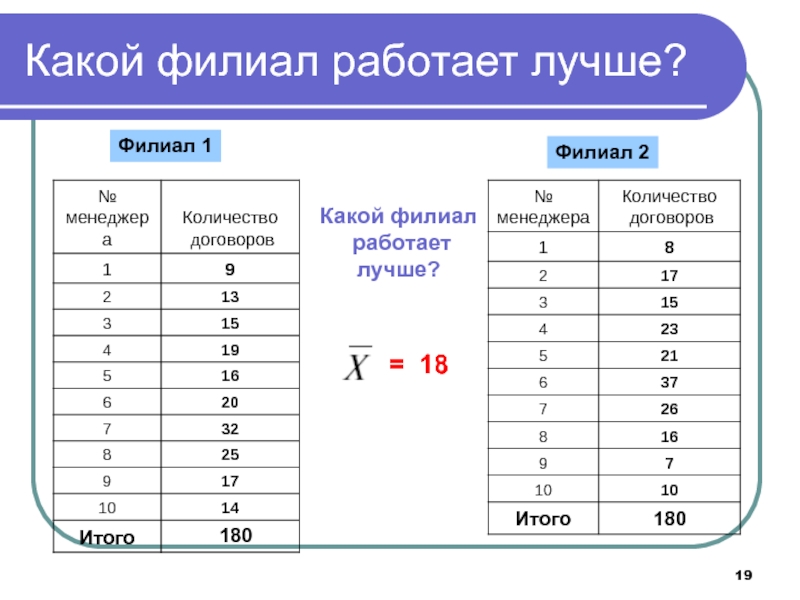
- 18. Какой филиал работает лучше?Филиал 1Филиал 2Какой филиал работаетлучше?
- 19. Какой филиал работает лучше?Филиал 1Филиал 2Какой филиал работаетлучше?= 18 180180
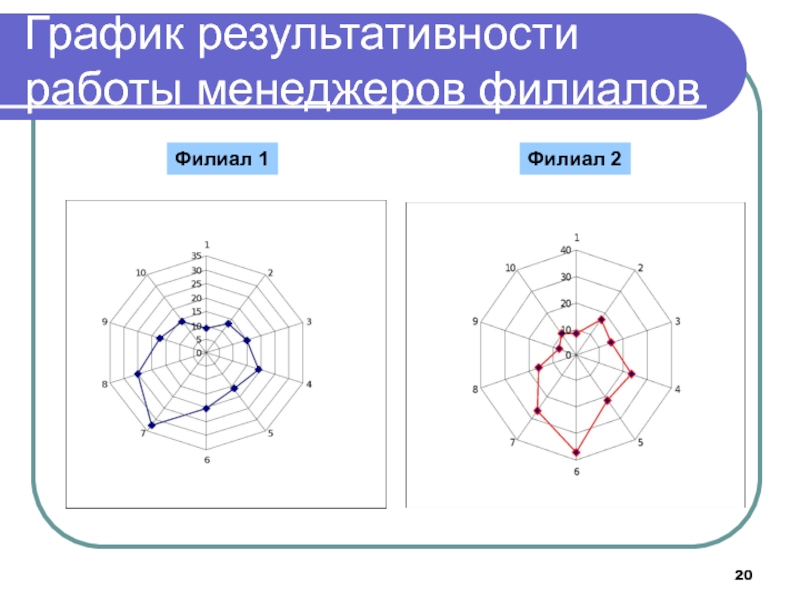
- 20. График результативности работы менеджеров филиаловФилиал 1Филиал 2
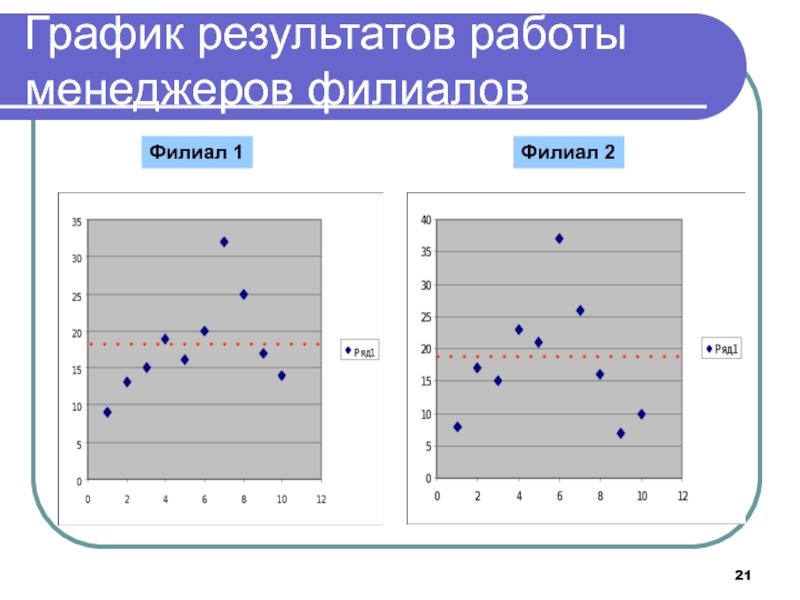
- 21. Филиал 1Филиал 2График результатов работы менеджеров филиалов
- 22. Размах вариацииРазмах вариации — это разность между
- 23. Расчет размаха вариации результатов работы менеджеров филиаловФилиал
- 24. Задача анализа вариацииВариацию можно определить как степень
- 25. Филиал 1Филиал 2График результатов работы менеджеров филиалов
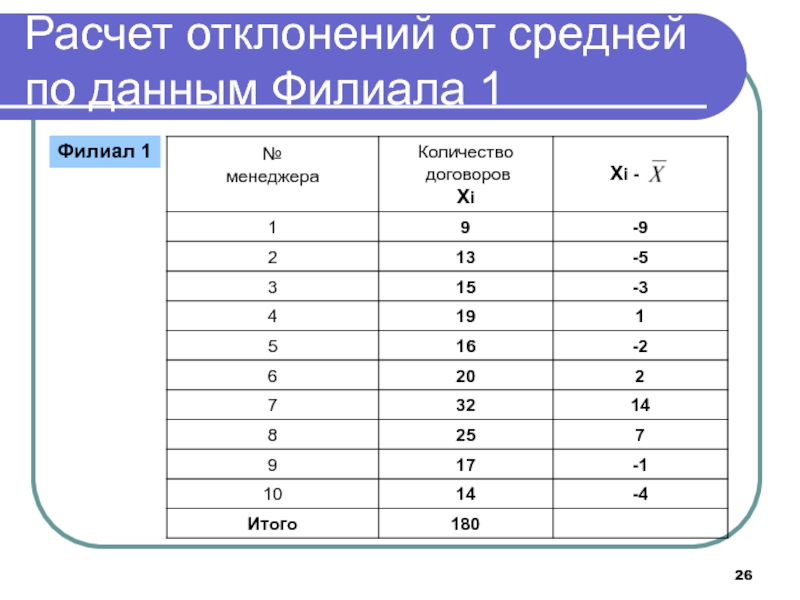
- 26. Расчет отклонений от средней по данным Филиала 1Филиал 1
- 27. Свойства средней арифметическойСвойство средней арифметической величины: Сумма
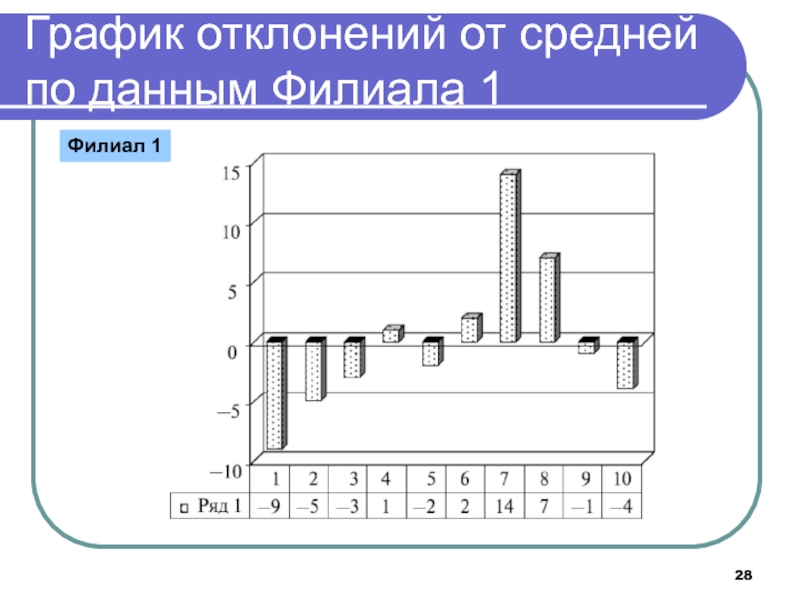
- 28. График отклонений от средней по данным Филиала 1Филиал 1
- 29. Мера вариацииМерой вариации будет служить средняя величина
- 30. Свойства средней арифметическойСвойство средней арифметической величины:Сумма квадратов
- 31. Система показателей вариации
- 32. Среднее линейное отклонениеСреднее линейное отклонение показывает стандартное
- 33. = 48 : 10 = 5Филиал 1Филиал
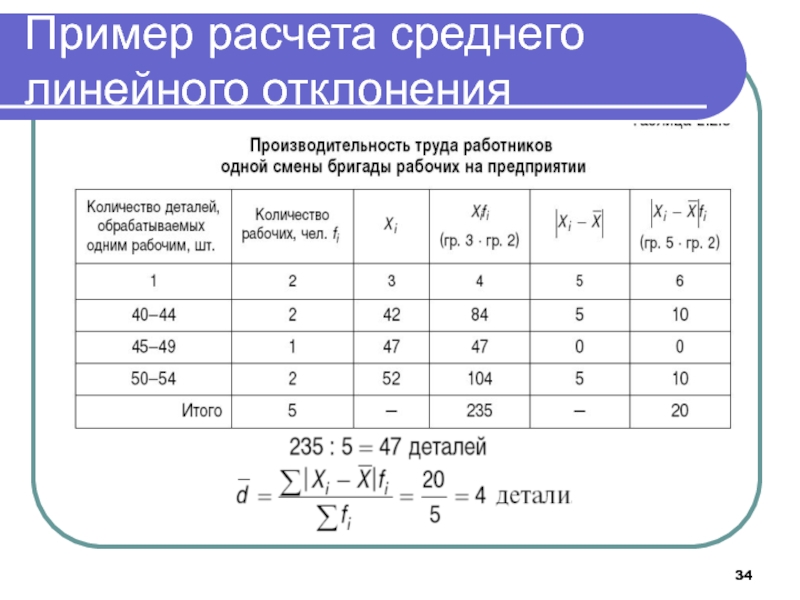
- 34. Пример расчета среднего линейного отклонения
- 35. ДисперсияДисперсия — это среднее арифметическое из квадратов
- 36. Филиал 1Филиал 2386 : 10 = 38,6758 : 10 = 75,8Расчет дисперсии результатов работы менеджеров филиалов
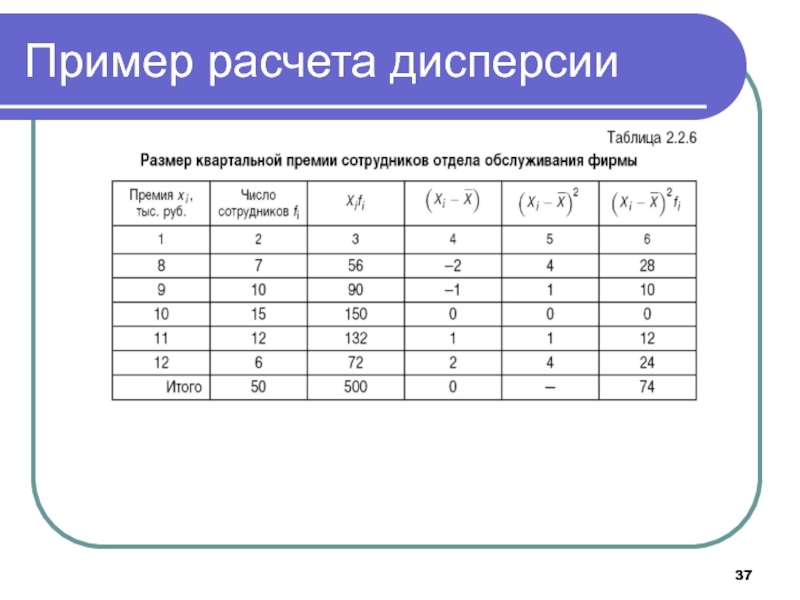
- 37. Пример расчета дисперсии
- 38. Пример расчета дисперсии
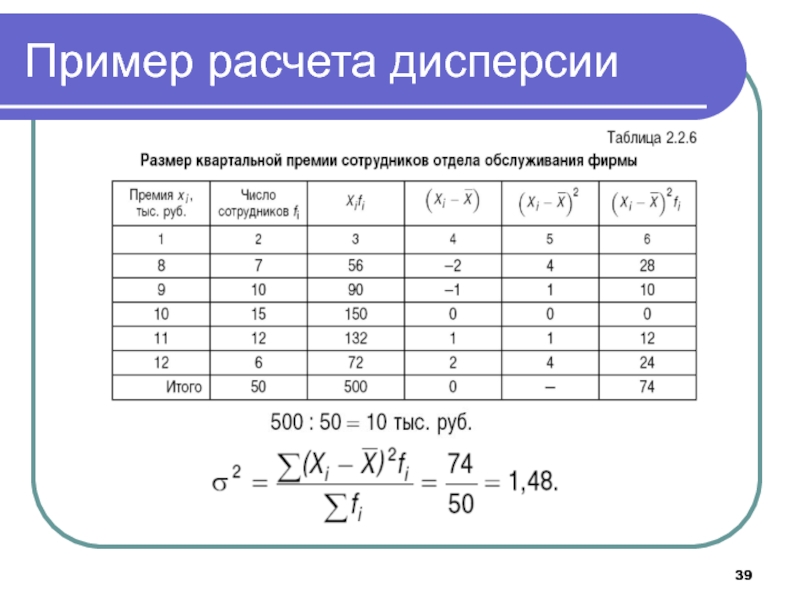
- 39. Пример расчета дисперсии
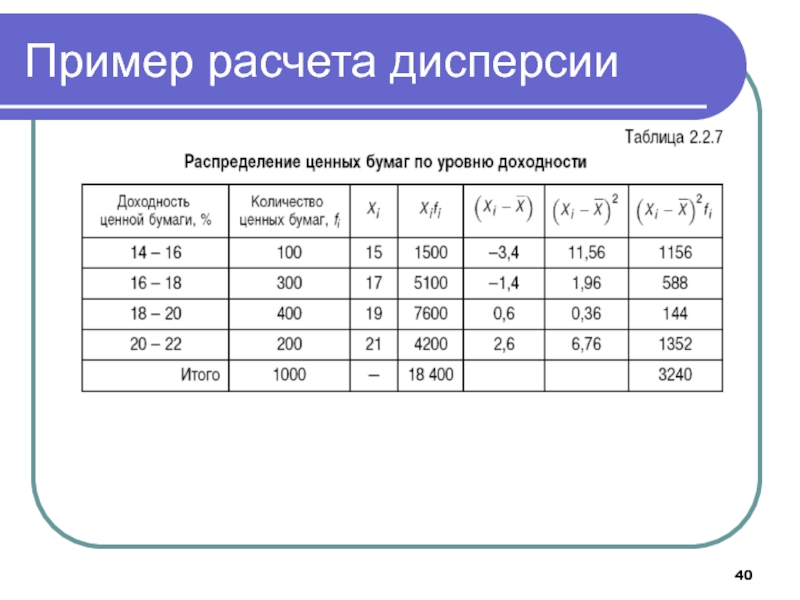
- 40. Пример расчета дисперсии
- 41. Пример расчета дисперсии
- 42. Пример расчета дисперсии
- 43. Среднеквадратическое отклонениеСреднее квадратическое отклонение (СКО) (в
- 44. Филиал 1Филиал 238,675,86,2 = 68,7 = 9Расчет среднеквадратического отклонения результатов работы менеджеров филиалов
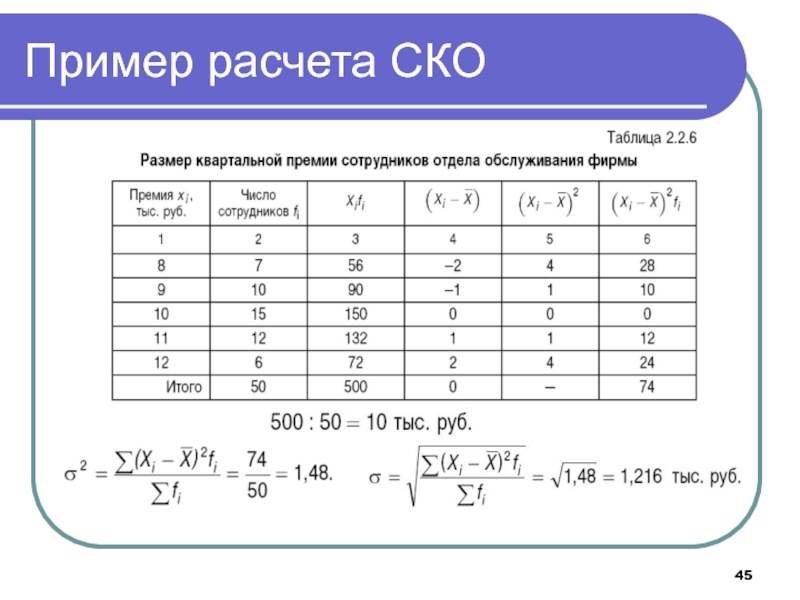
- 45. Пример расчета СКО
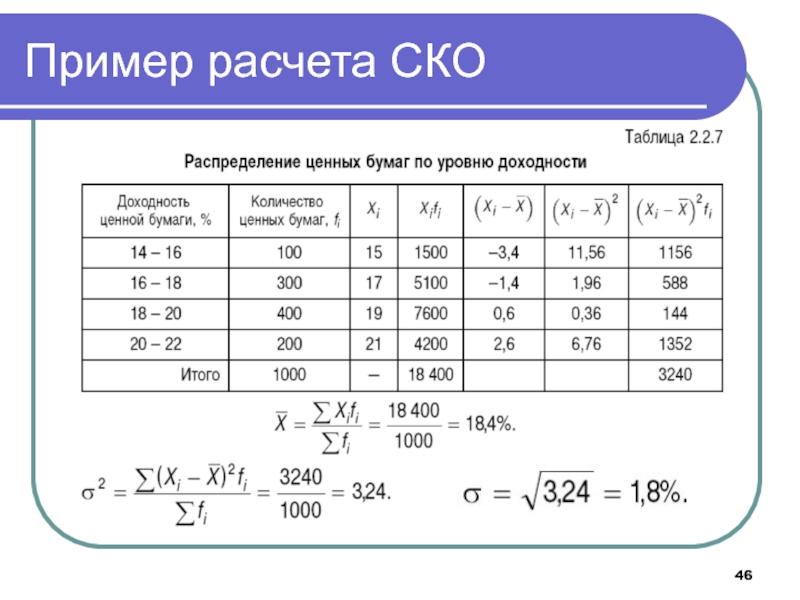
- 46. Пример расчета СКО
- 47. Относительные показатели вариацииОтносительные показатели вариации рассчитывают как
- 48. Линейный коэффициент вариацииЛинейный коэффициент вариации характеризует долю
- 49. Линейный коэффициент вариацииЛинейный коэффициент вариации характеризует долю
- 50. Коэффициент вариацииКоэффициент вариации рассчитывается как отношение среднего
- 51. Филиал 1Филиал 269VG = 6 / 18
- 52. Практическое заданиеРешаем задачу 1, Учебник, стр.138-139По данным
- 53. Практическое заданиеРешаем задачу 4, Учебник, стр. 141Определите
- 54. ИПЗ№1 по теме показатели вариацииРешаем задачу 5,
- 55. Практическое заданиеРешаем задачу 2, Учебник, стр. 139Определите
- 56. Готовимся к ИКР !!!!Оцените количественную однородность распределения
- 57. Групповое практическое заданиеРешите задачу 3, Учебник, стр.140Определите
- 58. Домашнее задание №6 1. Повторите материал темы
- 59. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Установочная лекция №5
Дисциплина «Статистика»
30.10.2014 и 13.11.2014
ДКП-2, 1
Московский финансово-промышленный университет «СИНЕРГИЯ»
Кафедра
Бизнес - статистики
Слайд 2План работы
1. Окончание разбора темы «Структурные средние»
2. Решение задач по
теме «Структурные средние»
3. Изучение новой темы «Показатели вариации»
Слайд 3Тема 6 – Средние величины (окончание)
Основные вопросы:
Расчет моды и медианы
по интервальному ряду распределения
Решение задач на расчет структурных средних.
Слайд 4Давайте вспомним, что
К основным структурным средним относятся …
и
Мо
Ме
Мода – это
значение или вариант признака, встречающийся чаще других, то есть вариант, который имеет максимальную частоту fi
Медиана – это
серединное значение, то есть вариант
признака, находящийся в середине упорядоченного (по возрастанию или убыванию) ряда вариантов и делящий объекты
совокупности (или группы) пополам.
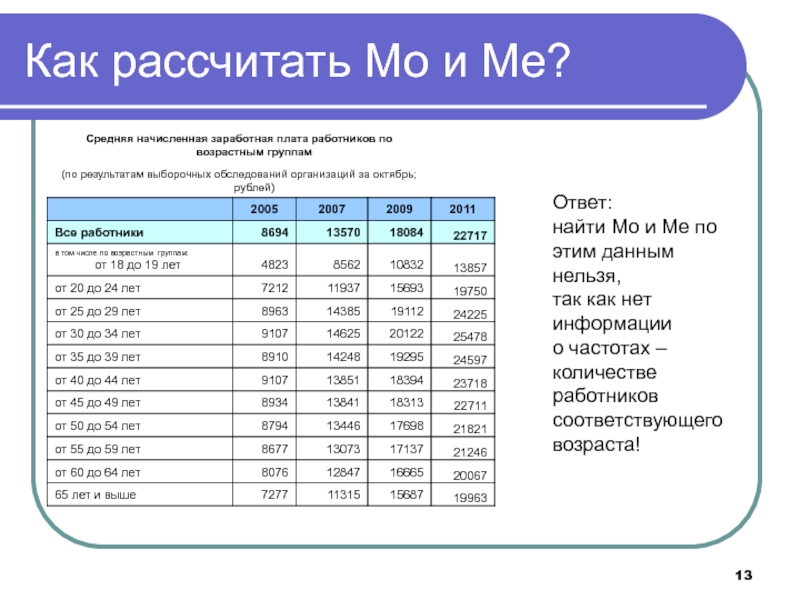
Слайд 13Как рассчитать Мо и Ме?
Ответ:
найти Мо и Ме по
этим данным нельзя,
так как нет
информации
о частотах – количестве работников
соответствующего возраста!
Слайд 16Тема 7: Показатели вариации
План
Роль показателей вариации в описании выборочной совокупности.
Основные
виды показателей вариации и методы их расчета.
Слайд 17В каком случае правомерно оценивать вариацию?
Вариация от лат. variatio —
изменение, различие.
Слайд 22Размах вариации
Размах вариации — это разность между наибольшим (Xmax )
и
наименьшим (Xmin ) значениями вариантов признака.
R
= Xmax – Xmin. Размах показывает границы и ширину диапазона вариации признака в совокупности или в выборке.
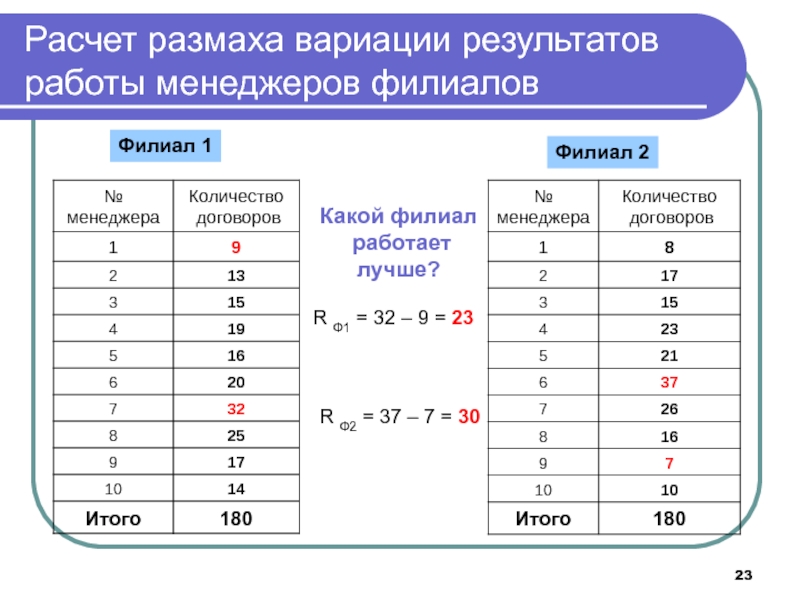
Слайд 23Расчет размаха вариации результатов работы менеджеров филиалов
Филиал 1
Филиал 2
Какой филиал
работает
лучше?
R Ф1 = 32 – 9 = 23
R Ф2 =
37 – 7 = 30Слайд 24Задача анализа вариации
Вариацию можно определить как степень различия между отдельными
значениями показателя у различных единиц внутри выборки.
Задача анализа вариации– обобщить
индивидуальные различия изучаемых единицСлайд 27Свойства средней арифметической
Свойство средней арифметической величины:
Сумма отклонений индивидуальных значений
признака от средней
арифметической равна нулю:
Слайд 29Мера вариации
Мерой вариации будет служить средняя величина из отклонений
_______
Xi
-
| Xi – |
( Xi –
)2Линейные показатели вариации
Квадратические показатели вариации
Слайд 30Свойства средней арифметической
Свойство средней арифметической величины:
Сумма квадратов отклонений индивидуальных значений
признака от средней арифметической меньше, чем сумма квадратов их отклонений
от любой другой произвольной величины С.Слайд 32Среднее линейное отклонение
Среднее линейное отклонение показывает стандартное отличие значения каждого
варианта от общей средней величины и определяется как
средняя
арифметическая из отклонений индиви-дуальных значений от средней, без учета их знака (по модулю)По несгруппированным данным
По сгруппированным данным
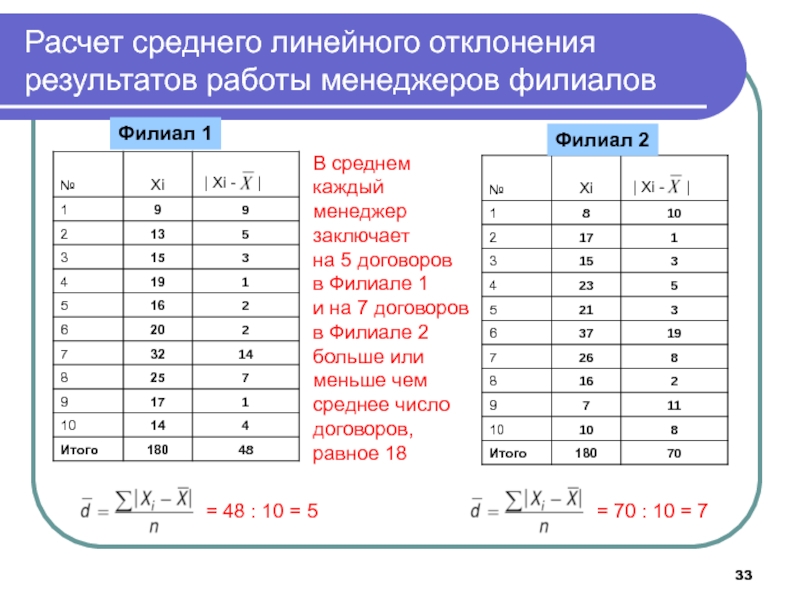
Слайд 33= 48 : 10 = 5
Филиал 1
Филиал 2
= 70 :
10 = 7
Расчет среднего линейного отклонения результатов работы менеджеров филиалов
В
среднемкаждый
менеджер
заключает
на 5 договоров
в Филиале 1
и на 7 договоров
в Филиале 2
больше или
меньше чем
среднее число
договоров,
равное 18
Слайд 35Дисперсия
Дисперсия — это среднее арифметическое из квадратов отклонений каждого значения
признака от общей средней. Дисперсия обычно называется средним квадратом отклонений
и обозначается .По несгруппированным данным
По сгруппированным данным
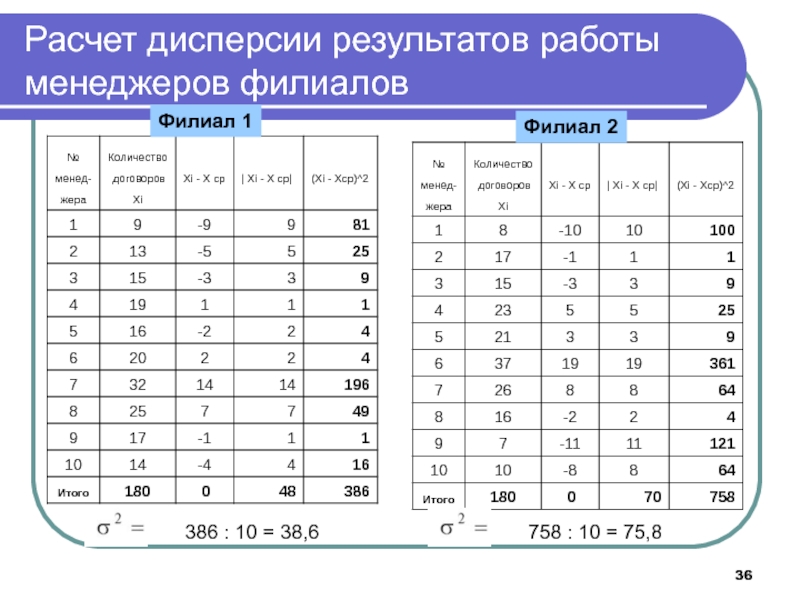
Слайд 36Филиал 1
Филиал 2
386 : 10 = 38,6
758 : 10 =
75,8
Расчет дисперсии результатов работы менеджеров филиалов
Слайд 43 Среднеквадратическое отклонение
Среднее квадратическое отклонение (СКО) (в литературе также используется
термин «стандартное отклонение») представляет собой квадратный корень из дисперсии и
обозначаетсяСКО показывает, на сколько в среднем отличается значение каждого варианта признака от среднего значения для данной совокупности или выборки.
.
По несгруппированным данным
По сгруппированным данным
Используем формулы средней квадратической величины
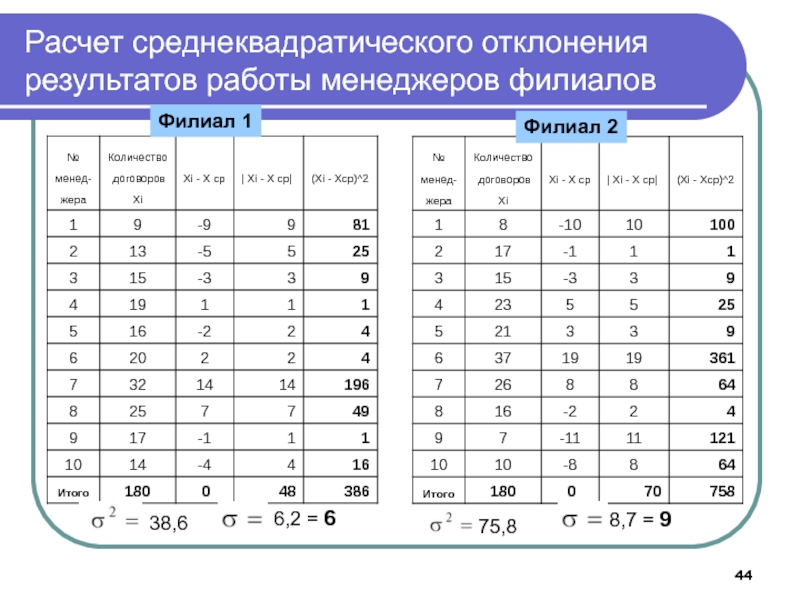
Слайд 44Филиал 1
Филиал 2
38,6
75,8
6,2 = 6
8,7 = 9
Расчет среднеквадратического отклонения результатов
работы менеджеров филиалов
Слайд 47Относительные показатели вариации
Относительные показатели вариации рассчитывают как отношение типичного отклонения
к средней величине, выраженное в %.
Различают:
Линейный коэффициент вариации ( V )Коэффициент вариации ( V G )
Слайд 48Линейный коэффициент вариации
Линейный коэффициент вариации характеризует долю среднего линейного отклонения
от общего среднего значения и рассчитывается по формуле
V
=
Слайд 49Линейный коэффициент вариации
Линейный коэффициент вариации характеризует долю среднего линейного отклонения
от общего среднего значения и рассчитывается по формуле
V
=
Слайд 50Коэффициент вариации
Коэффициент вариации рассчитывается как отношение среднего квадратического отклонения к
среднему значению:
Совокупность считается однородной, если коэффициент вариации не превышает 33%.
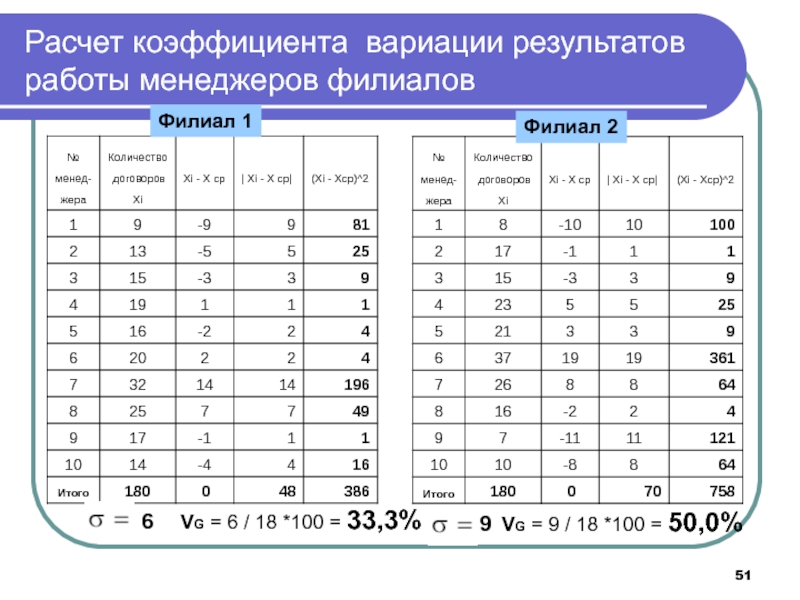
Слайд 51Филиал 1
Филиал 2
6
9
VG = 6 / 18 *100 = 33,3%
VG
= 9 / 18 *100 = 50,0%
Расчет коэффициента вариации результатов
работы менеджеров филиаловСлайд 52Практическое задание
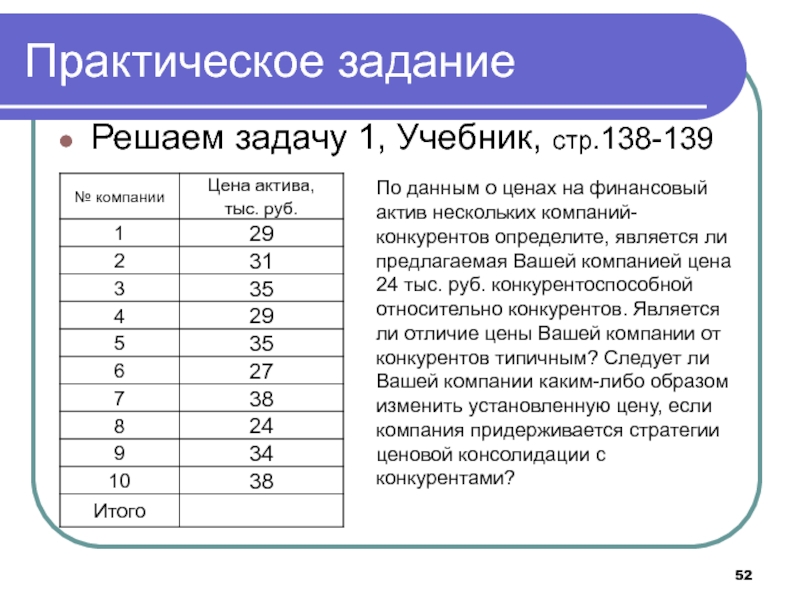
Решаем задачу 1, Учебник, стр.138-139
По данным о ценах на
финансовый актив нескольких компаний-конкурентов определите, является ли предлагаемая Вашей компанией
цена 24 тыс. руб. конкурентоспособной относительно конкурентов. Является ли отличие цены Вашей компании от конкурентов типичным? Следует ли Вашей компании каким-либо образом изменить установленную цену, если компания придерживается стратегии ценовой консолидации с конкурентами?Слайд 53Практическое задание
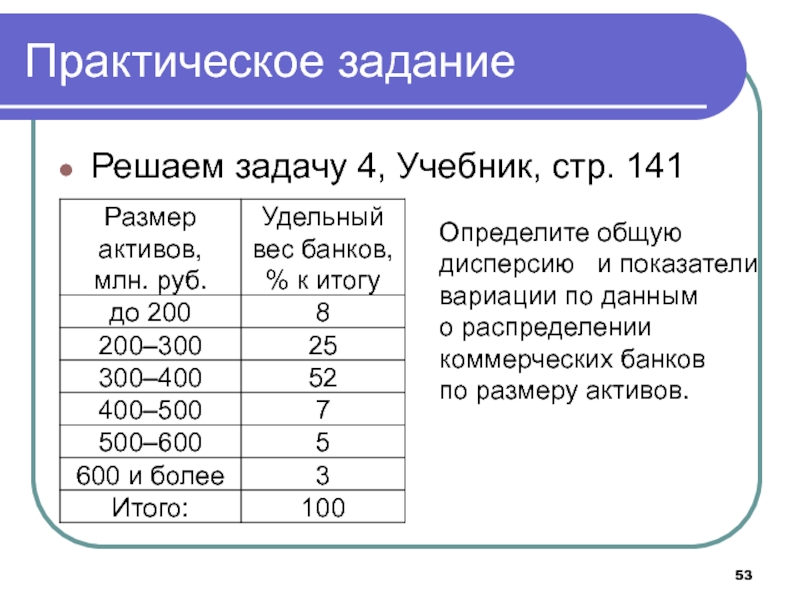
Решаем задачу 4, Учебник, стр. 141
Определите общую
дисперсию
и показатели
вариации по данным
о распределении
коммерческих банков
по размеру
активов.Слайд 54ИПЗ№1 по теме показатели вариации
Решаем задачу 5, Учебник, стр. 141
Оцените
однородность совокупности строительных фирм по объему инвестиций.
Слайд 55Практическое задание
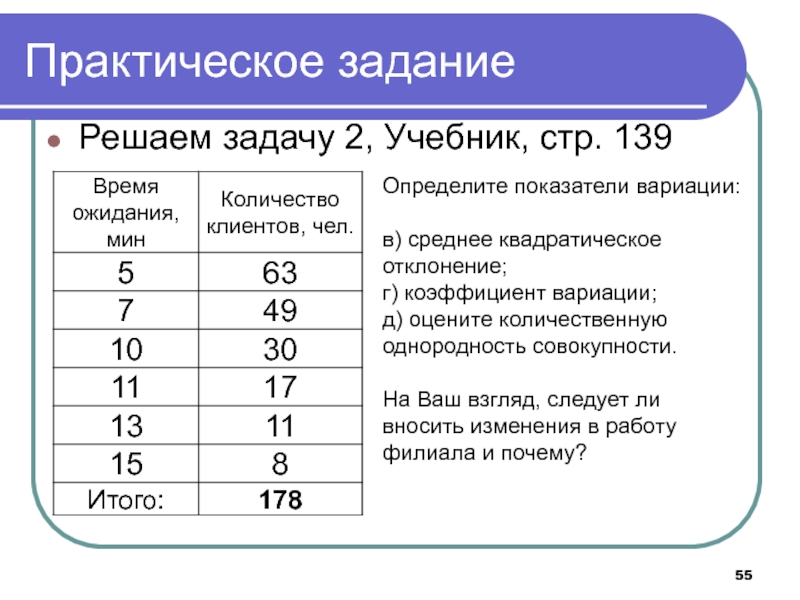
Решаем задачу 2, Учебник, стр. 139
Определите показатели вариации:
в) среднее
квадратическое отклонение;
г) коэффициент вариации;
д) оцените количественную однородность совокупности.
На Ваш взгляд, следует
ли вносить изменения в работу филиала и почему?Слайд 56Готовимся к ИКР !!!!
Оцените количественную однородность распределения торговых предприятий по
величине товарооборота. Сделайте выводы также по величине СКО.
Слайд 57Групповое практическое задание
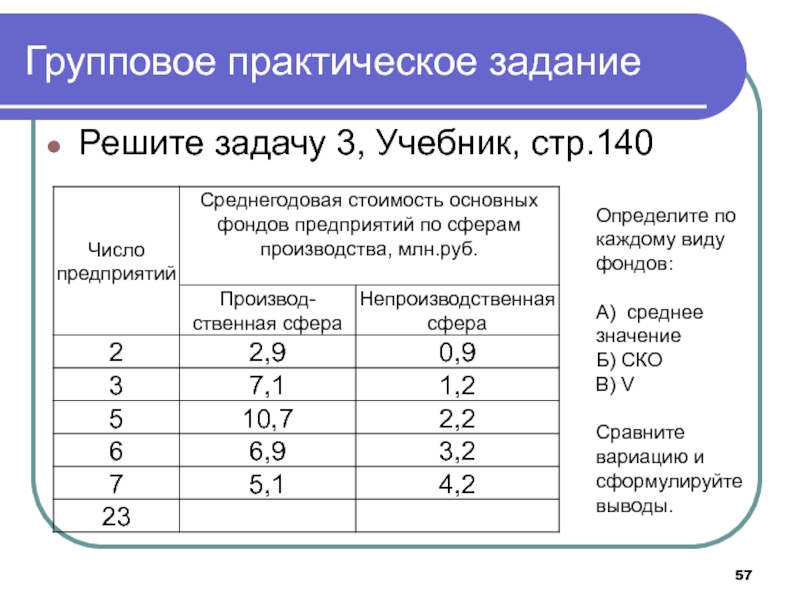
Решите задачу 3, Учебник, стр.140
Определите по
каждому виду
фондов:
А)
среднее
значение
Б) СКО
В) V
Сравните
вариацию и
сформулируйте
выводы.
Слайд 58Домашнее задание №6
1. Повторите материал темы 7 «Показатели вариации» по
настоящей презентации и Учебнику (с.120-131)
2. Решите задачи (срок сдачи не
позднее 11.12.2014):№13 (с.117), №14 (с.118), №3 (с.140)
НАПОМИНАЮ: 27.11.2014 у нас состоится АКР (аудиторная контрольная работа) по теме «Показатели вариации», результаты которой сильно влияют на итоговую оценку по курсу. Пожалуйста, позаботьтесь не опоздать к началу занятия и повторить теоретический материал и примеры из презентации!
Желаю Вам успехов!
С уважением, Е.В.Улитина