Валентинов В.А. Эконометрика. Лекция 20. Модели стационарных и нестационарных

временных рядов и их идентификация (модуль 5)
20.1. Определение строго стационарных

временных рядов
20.2. Проверка стационарности временных рядов
20.3. Модели стационарных временных рядов
20.4. Модели нестационарных временных рядов

временных рядов и их идентификация (модуль 5)
20.1. Определение строго стационарных

временных рядов
Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.
Временной ряд Уt (t=1, 2,…, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений  y1, y2,…, yn такое же, как и n наблюдений y1+ τ, y2+ τ,…, yn+ τ при любых n, t, τ.
Где ряды y1, y2,…, yn и y1+τ , y2+τ,…, yn+τ. являются сдвинутыми относительно друг друга на τ единиц или с лагом τ.
Таким образом, свойства строго стационарных рядов не зависят от момента времени t, т.е. в таких рядах от момента времени t не зависят закон распределения и числовые характеристики временного ряда.
Временной ряд имеет три характеристики:
- среднее значение,
- дисперсия,
автокорреляция.
Временной ряд будет стационарен, если среднее значение будет одинаковым на любом его отрезке, дисперсия временного ряда будет одинаковой на любом его отрезке или гомоскедастичной (однородной, одинаковой), автокорреляция является постоянной на любом участке временного ряда и зависит только от величины лага τ.

временных рядов и их идентификация (модуль 5)
Временной ряд называется нестационарным,

если характеристики временного ряда среднее значение, дисперсия, автокорреляционная функция зависят от времени. Например, если среднее значение временного ряда линейно зависит от времени, то это означает наличие во временном ряду линейной тенденции,
если дисперсия временного ряда изменяется во времени или является гетероскедастичной (неоднородной),
если автокорреляционная функция циклически изменяется, то это говорит о том, что временной ряд содержит периодические составляющие.

временных рядов и их идентификация (модуль 5)
20.2. Проверка стационарности временных

рядов
Проверка стационарности временного ряда по характеристике среднее значение.
Проверим на стационарность временной ряд по характеристике: среднее значение.
Выдвигается нулевая гипотеза о том, что среднее значение временного ряда является константой или коэффициент а1 линейной модели равен нулю.
Нулевую гипотезу H0: а1=0 проверим с помощью критерия Стьюдента для коэффициента а1 линейной модели Уt = а0+а1*t + et.
Расчеты характеристик модели можно выполнить с помощью функции ЛИНЕЙН.
Если нулевая гипотеза принимается, то считается, что временной ряд имеет среднее значение, не изменяющееся во времени, т.е. временной ряд не содержит возрастающей или снижающейся тенденции, но это не исключает наличие периодической составляющей.

временных рядов и их идентификация (модуль 5)
Проверка стационарности временного ряда

по характеристике автокорреляции.
Стационарный временной ряд не должен содержать одну или несколько периодических составляющих.
Периодическая составляющая проверяется с помощью визуального анализа графика временного ряда и с помощью автокорреляционной функции. Если в автокорреляционной функции наблюдается локальный минимум или максимум, то это указывает на наличие во временном ряду периодической составляющей.

временных рядов и их идентификация (модуль 5)
Проверка стационарности временного ряда

по признаку дисперсии временного ряда.
Проверку нулевой гипотезы о том, что дисперсии временного ряда одинаковы на любом отрезке (гомоскедастичны), осуществим по критерию Фишера.
Разделим временной ряд на три равных участка, на первом и третьем участке вычислим дисперсии временного ряда и сравним между собой по критерию Фишера. Если фактическое значение критерия Фишера будет больше табличного, то нулевая гипотеза отвергается и утверждается, что дисперсии временного ряда являются гетероскедастичными.
 

временных рядов и их идентификация (модуль 5)
20.3. Модели стационарных

временных рядов
Если временной ряд стационарен, то это означает, что численные значения временного ряда изменяются около среднего значения с примерно одинаковой амплитудой без четко выраженных периодических колебаний.
Стационарные временные ряды могут получаться после моделирования нестационарного временного ряда, остатки которого являются стационарными.
К основным линейным моделям стационарных временных рядов относятся:
1) модели авторегрессии;
2) модели скользящего среднего;
3) модели авторегрессии и скользящего среднего.

временных рядов и их идентификация (модуль 5)
Модели авторегрессии
Уровень временного ряда,

представленного моделью авторегрессии порядка р, можно представить следующим образом:
Уt=δ1Уt-1+δ2Уt-2+…+δpУt–p+νt,
где p – порядок модели авторегрессии;
δt – коэффициенты модели авторегрессии, подлежащие оцениванию;
νt – белый шум (случайная величина с нулевым математическим ожиданием).
Модель авторегрессии порядка р обозначается как АР(р) или AR(p).
На практике чаще всего используются модели авторегрессии первого, второго, максимум третьего порядков.
Модель авторегрессии первого порядка АР(1) называется «Марковским процессом», потому что значения переменной У в текущий момент времени t зависят только от значений переменной У в предыдущий момент времени (t–1). Данная модель имеет вид:
Уt=δУt–1+νt.
Модель авторегрессии второго порядка АР(2) называется «процессом Юла». Данная модель имеет вид:
Уt=δ1Уt-1+δ2Уt-2+νt.

временных рядов и их идентификация (модуль 5)
Модели скользящего среднего

Модели скользящего среднего относятся к простому классу моделей временных рядов с конечным числом параметров, которые можно получить, представив уровень временного ряда как алгебраическую сумму членов ряда белого шума с числом слагаемых q.
Общая модель скользящего среднего порядка q имеет вид:
Уt=νt–φ1νt–1–φ2νt–2–…–φqνt–q,
где q – порядок модели скользящего среднего;
φt – неизвестные коэффициенты модели, подлежащие оцениванию;
νt – белый шум.
Модель скользящего среднего порядка q обозначается как CC(q) или MA(q).
На практике чаще всего используются модели скользящего среднего первого CC(1) и второго порядков CC(2).
Коэффициенты модели скользящего среднего порядка q не обязательно должны в сумме давать единицу и не обязательно должны быть положительными.
Качество модели скользящего среднего зависит от белого шума, который можно получить с помощью функции Ехсе1. Если полученный белый шум как - то напоминает временной ряд, то качество модели получается хорошим, в противном случае не удается построить достоверную модель скользящего среднего.

временных рядов и их идентификация (модуль 5)
Модели авторегрессии и

скользящего среднего
Для достижения большей гибкости модели временных рядов при эконометрическом моделировании в неё включают как члены авторегрессии, так и члены скользящего среднего.
Подобные модели получили название смешанных моделей авторегрессии и скользящего среднего и также относятся к линейным моделям стационарных временных рядов.
Смешанная модель авторегрессии и скользящего среднего обозначается как АРСС(p,q) или ARMA(p,q).
Чаще всего на практике используется смешанная модель АРСС(1) с одним параметром авторегрессии p=1 и одним параметром скользящего среднего q=1.
Данная модель имеет вид:
Уt=δУt–1+νt–φνt–1,
где δ – параметр процесса авторегрессии;
φ – параметр процесса скользящего среднего;
νt – белый шум.

временных рядов и их идентификация (модуль 5)
20.4. Модели нестационарных временных

рядов
Если временной ряд нестационарен, то это означает, что временной ряд содержит или линейную тенденцию или гетероскедастичность остатков или автокорреляцию остатков или периодическую составляющую или все вместе.
Рассмотрим следующие модели нестационарных временных рядов.
Модель периодических составляющих временных рядов.
Модель гетероскедастичности временных рядов.
Модель автокорреляции остатков.

временных рядов и их идентификация (модуль 5)
Модель периодических составляющих временных

рядов
Представим временной ряд в виде аддитивной модели, имеющей следующие компоненты:
Уt = f1t + f2t+ f3t + et.
Моделирование тренда f1t
Включение в модель Уt = f1t + et тренда преследует две цели:
первая – определить долговременную тенденцию временного ряда для получения долгосрочных прогнозов;
вторая – преобразование нестационарного временного ряда в стационарный, для выделения в них периодических составляющих.
Тренд f1t обычно воспроизводится с помощью следующих математических функций, которые слабо искажают периодические составляющие:
f1t= a0 + a1*t,
f1t= a0 + a1*lnt,
f1t= a0 + a1/t.
Наибольшее распространение получила линейная функция, так как она не оказывает влияния на периодическую составляющую временного ряда.
Все остальные функции искажают периодическую составляющую временного ряда, поэтому не получили широкого применения.
Коэффициенты модели Уt = f1t + et определяются методом наименьших квадратов.

временных рядов и их идентификация (модуль 5)
Моделирование сезонной и циклических

компонент (f2t, f3t).
Сезонная и циклическая компоненты являются периодическими с разными периодами.
Обычно в экономических временных рядах на длинно периодическую циклическую составляющую накладывается сезонная волна.
Можно предложить методику определения всех периодических составляющих временного ряда, в том числе сезонных и циклических, определить их достоверность и затем их включить в модель.
Процесс моделирования сезонной и циклической компонент выполняется в следующей последовательности.
Шаг 1. Выбор модели для выявления периодических составляющих.
Для выявления периодических составляющих временного ряда используется следующая модель:
Уt = a0 + a1*t + a2*Sin(2t/T) + a3*Cos(2t/T) + et,
где а0, а1, а2, а3 – коэффициенты, определяемые методом наименьших квадратов;
(а0 + а1*t) = ft – линейная функция (тренд), которая приводит временной ряд к стационарному виду с нулевым средним значением, без искажения периодических составляющих остатка;
Sin(2t/T), Cos(2t/T) – тригонометрические функции периодической составляющей временного ряда, сумма которых позволяет учесть начальную фазу колебания;
t – порядковый номер времени;
Т – период или длина волны циклической составляющей временного ряда.

временных рядов и их идентификация (модуль 5)
Длительность периода Т исследователь

задает в интервалах от трех единиц до удвоенной длины временного ряда. Дальнейшее увеличение длины волны приводит к тому, что небольшие отрезки этой волны начинают описывать нециклические тенденции временного ряда;
(2t/T) - аргумент тригонометрической функции, выраженный в радианах;
1/Т – частота, численно равная количеству колебаний в единицу времени;
Шаг 2. Создается база данных.
Х1 - t - время,
Х2 - Sin(2t/T),
Х3 - Cos(2t/T),
У - значения показателя временного ряда,
Т - период циклической составляющей, значение которого вводит исследователь в пределах от 3 до удвоенной длины временного ряда.
Шаг 3. Вычисление ошибки модели Е.
Вычисление ошибки модели Е
Уt = a0 + a1*t + a2*Sin(2t/T) + a3*Cos(2t/T) + et
с помощью статистической функции ЛИНЕЙН.
Переход к шагу 2 с изменением периода Т.
Шаг 4. Построение периодограммы - графика зависимости ошибки модели Е временного ряда от периода Т циклического фактора, включенного в модель.
Строится периодограмма - график зависимости Е от Т.

временных рядов и их идентификация (модуль 5)
Шаг 5. Определение периодических

составляющих временного ряда.
Определяются такие значения периодов Т, при которых ошибка модели имеет локальные минимумы. Обнаруженные периоды характеризуют периодические составляющие временного ряда, среди которых надо исключить ложные периоды. Ложная периодичность относится к периодам (эхам), которые являются кратными величине основного периода. Основной период имеет наименьшую ошибку модели, а кратные периоды или ложные периоды имеют большую ошибку модели. Например, квартальная периодическая составляющая (3 месяца) порождает эхо на периодах: 3*2=6 месяцев или полугодовой период, 3*3 =9 месяцев, 3*4 =12 месяцев или годовой период и т.д.
Шаг 6. Определение достоверных периодических составляющих временного ряда.
Для определения достоверных периодических составляющих необходимо построить модель с участием всех обнаруженных периодических составляющих и по критерию Стьюдента определить достоверность коэффициентов, стоящих перед тригонометрическими функциями, с использованием статистической функции ЛИНЕЙН Excel.
Для определения достоверности периодических составляющих строится модель вида:
Уt = a0 + a1*t + a2*Sin(2t/T1) + a3*Cos(2t/T1) + a4*Sin(2t/T2) + a5*Cos(2t/T2) + … + et,
где Т1 и Т2 - периоды выделенных периодических составляющих.
Анализ характеристик многофакторной модели производится обычным образом. Коэффициенты модели, достоверные по критерию Стьюдента, укажут на достоверность наличия соответствующей периодической составляющей временного ряда.

временных рядов и их идентификация (модуль 5)
Шаг 7. Построение модели

временного ряда.
Окончательная модель временного ряда с включением всех компонент может иметь следующий вид:
Уt = a0 + a1*t + a2*Sin(2t/T1) + a3*Cos(2t/T1) + a4*Sin(2t/T2) + a5*Cos(2t/T2) + et,
где a0 + a1t =f1t - тренд,
a2*Sin(2t/T1) + a3*Cos(2t/T1) = f2t – сезонная компонента,
Т1 = период сезонной компоненты,
a4*Sin(2t/T2) + a5*Cos(2t/T2) = f3t – циклическая компонента,
Т2 – период циклической компоненты.
еt – остатки модели.
Коэффициенты модели рассчитываются методом наименьших квадратов.

временных рядов и их идентификация (модуль 5)
Модель гетероскедастичности временных рядов

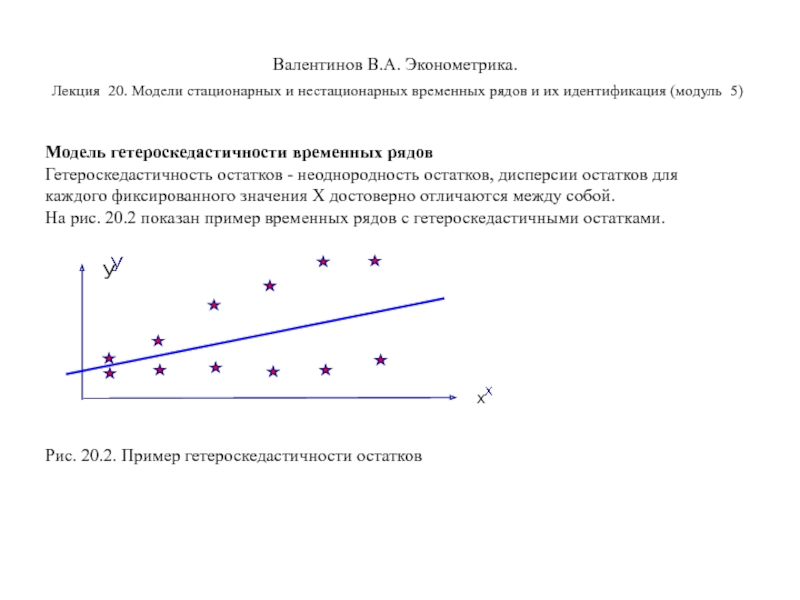
Гетероскедастичность остатков - неоднородность остатков, дисперсии остатков для каждого фиксированного значения Х достоверно отличаются между собой.
На рис. 20.2 показан пример временных рядов с гетероскедастичными остатками.









Рис. 20.2. Пример гетероскедастичности остатков

временных рядов и их идентификация (модуль 5)
Причины появления

гетероскедастичности остатков:
плохая спецификация модели,
наличие в базе данных двух и более групп объектов, свойства которых сильно отличаются между собой.
Последствия гетероскедастичности:
уравнение регрессии может описывать свойства тех объектов, которых вообще нет,
доверительные интервалы регрессии и прогноза не соответствуют фактическим значениям остатков.
Критерии проверки достоверности гетероскедастичности.
Для обнаружения гетероскедастичности используется:
- визуальный метод.
Для проверки достоверности гетероскедастичности используется:
- критерий Гольдфельда-Квандтома.
Критерий Гольдфельда-Квандтома использует критерий Фишера анализа двух дисперсий остатков, определенных для двух групп остатков, взятых определенным образом из совокупности всех остатков.

временных рядов и их идентификация (модуль 5)
Методы устранения гетероскедастичности остатков.
Известно

несколько методов устранения гетероскедастичности остатков:
- метод выделения однородных объектов,
- обобщенный метод наименьших квадратов или метод Эйткена.
Метод выделения однородных объектов.
Самый простой метод это выделение группировка однородных объектов, для которых остатки модели будут однородными.
Обобщенный метод наименьших квадратов или метод Эйткена.
Линейное регрессионное уравнение имеет следующий вид:
Уi = a0 + a1*XI + ei.
Если все уравнение разделить на модуль остатков ei, то для новых переменныхостатки новой модели будут принимать значения 1 или -1.
Следовательно, остатки новой модели будут гомоскедастичны.

временных рядов и их идентификация (модуль 5)
Модель автокорреляции остатков
Если из

временного ряда исключить линейную тенденцию
Уt –( а0 +а1*Хt) = et,
то остатки модели et, могут иметь следующие закономерности их поведения:
- быстро изменяться около среднего значения остатков, равных нулю;
- плавно изменяться по периодической функции;
- изменяться хаотично.
Если остатки модели имеют определенную закономерность в их изменении, то появляется возможность улучшить модель и повысить точность прогнозирования.
Анализ автокорреляции остатков проводился в теме 6.

временных рядов и их идентификация (модуль 5)
Модели, учитывающие автокорреляцию остатков
Если

линейная модель
Уt = а0 +а1*Хt + et
содержит автокорреляцию остатков первого порядка, то для ее устранения можно использовать следующую модель
Уt = а0 +а1*Хt + р*et-1 + vt,
где р - коэффициент автокорреляции первого порядка;
et-1- лаговая переменная остатков первого порядка;
еt = р*еt-1 + vt;
vt - остатки новой модели.
Интрига предложенной модели заключается в том, что одновременно нельзя найти коэффициенты а0, а1 и р.
Эконометристами были предложены несколько методов определения
коэффициентов модели
Уt = а0 +а1*Хt + р*et-1 + vt.
Рассмотрим наиболее простой - метод наименьших квадратов, который выполняется в следующей последовательности:
- методом наименьших квадратов определяются коэффициенты а0, а1 модели
Уt = а0 +а1*Хt + et
- вычисляются остатки модели
et = Уt - (a0 + a1*Xt)
- методом наименьших квадратов определяется коэффициент р модели
et = p*et-1 + vt.

временных рядов и их идентификация (модуль 5)
Прогнозирование по

модели с коэффициентом автокорреляции производится по формуле
У пр(n+1) = a0 + a1*X(n+1) + p*e(n),
где Упр( n+1) - прогнозное значение зависимой переменной на прогнозный период,
e(n) - значение остатка в предшествующий период.
а0 +а1*Х(n +1) - обычный прогноз по линейной функции,
р*е(n) - поправка прогноза на автокорреляцию остатка.
Улучшение прогноза с использованием автокорреляции остатков первого порядка возможно только при прогнозировании на одну дату.