Слайд 1Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Допущения модели: Будем считать, что при постоянном расходе – Q,
разделяемой дисперсной системы, поступающей в классификатор, кинетическая стадия эволюции рассматриваемого процесса закончилась еще при вводе разделяемой дисперсной системы в аппарат. В результате чего, в рабочей части классификатора установилось равновесное (стационарное) распределение по скоростям потока и происходит относительно медленное изменение во времени гидродинамических параметров рассматриваемой дисперсной системы. Гидродинамические процессы классификации (как и любые другие процессы переноса) имеют стохастическую природу, и в их основе лежат, как детерминированные, так и вероятностно-статистические явления.
Определяя стохастические составляющие процесса, будем полагать, что случайные силовые воздействия на частицу дисперсной фазы системы в различные моменты времени статистически независимы (δ-коррелированы во времени) и меняются гораздо быстрее, чем вызываемые ими изменения наблюдаемых величин. Кроме того, будем предполагать, что система не обладает "памятью" и вероятность её нахождения в некотором состоянии в данный момент времени полностью определяется состоянием системы в некоторый предшествующий момент времени.

Слайд 2Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Другими словами, будем считать, что в цилиндрической рабочей части классификатора
имеет место квазиустановившееся стохастическое движение частиц дисперсной фазы, которое соответствует теории случайных марковских процессов.
Тогда основная задача теоретических исследований будет заключаться в выводе явного выражения для некой функции распределения, характеризующей состояние системы на гидродинамической стадии её эволюции, а также в получении зависимостей, определяющих параметры системы.
Считая разделяемую дисперсную систему малоконцентрированной, введем цилиндрическую систему координат, связанную с осью симметрии классификатора. Учитывая, быстрое завершение кинетической стадии эволюции системы будем считать, что тангенциальные скорости дисперсионной среды (несущей фазы) и частиц дисперсной фазы практически совпадают.
Слайд 3Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Если рассматривать криволинейное движение стоксовской сферической частицы массы mч и
диаметра dч в подвижной системе координат, то скорость частицы:
где – скорость дисперсионной среды (потока), – относительная скорость движения частицы, а ее ускорение определяется теоремой Кориолиса в виде:
(1)
где t – время, ρч и ρс – плотность частиц и среды соответственно, R – текущий радиус вращения (расстояние от оси аппарата), – угловая скорость вращения, μ0– динамическая вязкость дисперсионной среды, Σ – прочие силы, включая случайные составляющие всех сил.
Вывод: Каждый член левой части уравнения представляет собой некоторый компонент силы, с которой частица действует на поток, стремящийся искривить траекторию частицы и изменить ее скорость. В правой части уравнения представлена гидродинамическая сила, действием которой объясняется указанный эффект, т.е. внешняя сила сопротивления, определяемая формулой Стокса.
Слайд 4Первый член уравнения связан с ускорением классификационного движения и может
быть равен нулю при условии vс = const. Это возможно
только для практически безынерционных частиц, размеры которых не превышают 100 мкм. Для этих частиц, также можно считать пренебрежимо малыми величинами, составляющие силы сопротивления, обусловленные нестационарностью движения частиц, которые включены в состав сил Σ.
Второй член представляет собой центробежную силу (с учетом вытеснения частицей соответствующего объема дисперсионной среды), направленную по радиусу закругления потока.
Третий член уравнения выражает реакцию частицы, на тормозящее влияние среды при переходе частицы в более замедленные слои. Этот вектор по направлению всегда совпадает с . Для безынерционных частиц его можно исключить из рассмотрения.
Четвертый член представляет собой силу Кориолиса, которой также можно пренебречь, т.к. ωR >> dR/dt (скорость окружного движения много больше радиальной скорости частицы).
Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с инжекцией

Слайд 5Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
В результате для радиального движения частиц получаем:
(2)
где u’=u’(Q,R) –
средняя скорость радиального движения дисперсионной среды.
Воздействие дополнительного инжектируемого потока с расходом Qin учтем с помощью введения в выражение (2) некой дополнительной составляющей средней скорости радиального движения дисперсионной среды u”=u”(Qin,R). Тогда уравнение (2) можно записать в виде:
(3)
Для нахождения зависимости ω2 = ω2(R) воспользуемся известным законом распределения окружных скоростей w’ по радиусу вращения:
(4)
где w’0=w’(R0) – окружная скорость на входе в классификатор, R0 – радиус цилиндрической части классификатора, Sвх – площадь входного патрубка, n – некоторый постоянный показатель.
Слайд 6Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
В зависимости от конструктивных особенностей классификатора и свойств дисперсионной среды,
показатель n в этом уравнении может изменяться от –1 до +1. В первом случае, мы имеем дело с вынужденным движением, когда дисперсионная среда ведет себя как твердое тело и вращается с постоянной угловой скорость. Подобное поведение характерно для центральных слоев дисперсионной среды, расположенных в непосредственной близости от оси аппарата, примерно в пределах радиуса выходного патрубка R≈Rвых.
Для периферийных слоев R > Rвых, в уравнении (3) n, как правило, меняться в пределах от +0,5 до +1.
Последний случай соответствует свободной циркуляции по концентрическим окружностям, когда окружная скорость обратно пропорциональна радиусу и ее распределение определяется так называемым "законом площадей».
В дальнейшем, ограничимся рассмотрением лишь периферийных слоев классификатора и для определенности будем считать, что n [0,5; 1].
Поскольку w’=ωR, с учетом (4) имеем:
и после подстановки в выражение (3) получаем:
(5)
здесь – постоянная величина для данного диаметра частиц (при неизменных плотностях дисперсной фазы и дисперсионной среды).

Слайд 7Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Определим среднюю скорость радиального движения дисперсионной среды в виде:
(6)
где Q = const – расход основного потока дисперсной системы, поступающей в классификатор; γ0 – половинный угол раскрытия конусной части классификатора; kγ=kγ(Q) – постоянный коэффициент, определяющий (для заданного расхода Q) осредненное эффективное отклонение нисходящего потока от стенок цилиндрической части аппарата; L – длина цилиндрической рабочей части классификатора;
– постоянная величина (для данного расхода Q), характеризующая радиальный эффективный расход, приходящийся на единицу длины цилиндрической рабочей части классификатора.
По аналогии с выражением (6), представим дополнительное воздействие инжектируемого потока в виде:
(7)
где Qin = const – расход потока разделяемой дисперсной системы, инжектируемого в классификатор; kin=kin(Qin) – постоянный коэффициент, определяющий (для заданного расхода Qin) эффективность классификационного воздействия, с учетом конструктивного исполнения инжектора, Ain=kinQin/L – постоянная величина (для данного расхода Qin), характеризующая инжектируемый эффективный расход, приходящийся на единицу длины цилиндрической рабочей части классификатора.

Слайд 8Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Подстановка выражений (6) и (7) в уравнение (5) дает:
(8)
Вывод: При
выбранной обобщенной координате R, процессы классификационного воздействия инжектируемого потока и радиального движения дисперсионной среды являются подобными в том смысле, что uR=const.
Выберем новый параметр S = S(R) (новую обобщенную координату) таким образом, чтобы аналогичное подобие наблюдалось в поле действия центробежных сил:
Обозначая, Rn+1=S – новая обобщенная координата, для новой средней скорости движения частиц Wʹ в пространстве S, с подобием вида WʹS=const получаем:
где и – некоторые постоянные величины.
Слайд 9Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
С учетом сделанных допущений, рассмотрим поведение частиц дисперсной фазы разделяемой
дисперсионной системы в пространстве новых обобщенных координат.
Здесь наряду со средней скоростью процесса Wʹ, по-прежнему присутствует и случайная составляющая этой скорости – , влиянием которой пренебречь нельзя.
Тогда уравнение (9) предстает в виде:
(10)
Поскольку величина в уравнении (10) обусловлена наличием случайных сил, действующих на частицу со стороны потока дисперсионной среды, то естественно и скорость W, и координата S, тоже будут случайными величинами.
Вывод: Распределение частиц дисперсной фазы в радиальном направлении можно характеризовать лишь статистически, например, с помощью функции плотности распределения f = f(S, t), нормированной на единицу.
Слайд 10Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
По определению величина f(S,t)dS представляет собой вероятность того, что произвольно
выбранная частица постоянного диаметра dч будет иметь в момент времени t координату в интервале (S,S+dS).
Будем считать, что случайные составляющие скорости δ-коррелированы во времени и их свойства удовлетворяют допущениям теории случайных марковских процессов.
Кроме того, допускаем постоянство во времени средней скорости движения частиц Wʹ=WʹS и стационарность случайных возмущений, интенсивность которых охарактеризуем с помощью параметра B = B(S)= const в пространстве S.
Тогда, для описания гидродинамической стадии эволюции системы в пространстве S мы можем воспользоваться известным кинетическим уравнением Фоккера-Планка-Колмогорова (далее уравнение ФПК) в виде:
(11)
С учетом сделанных допущений, подстановка выражения (9) в уравнение (11) дает:
(12)
Слайд 11Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Уравнение такого же типа будет справедливым и для функции распределения
f по другим переменным, если только выполнены условия, лежащие в основе его вывода:
относительная малость изменения наблюдаемых величин в элементарных актах взаимодействия;
линейность по интегрального оператора, выражающего изменение функции благодаря этим актам.
Обозначив, B/2=b0, вводя безразмерную координату x=S/S0, получаем:
(13)
где – постоянная величина, а – постоянные коэффициенты, характеризующие интенсивность классификационного воздействия, центробежных сил и случайных возмущений, соответственно.
Слайд 12Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Функция f0(x), задающая начальное (в момент времени t=0) распределение частиц
данного размера в пространстве x, считается известной и удовлетворяющей в любой момент времени условию нормировки:
(15)
Последнее условие показывает, что функция f(x,t) должна быть ограниченной на интервале (0,∞), не иметь сингулярности в нуле и удовлетворять условию:
Перейдем к решению уравнения (13) с учетом сформулированных начальных и граничных условий. Воспользовавшись известным методом разделения переменных решение будем искать в виде:
Подставляя последнее выражение в (13) имеем:
(16)
Слайд 13Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
В начале обратимся к анализу предельного случая n=1, в результате
получаем:
(17)
где λ – набор некоторых постоянных величин, нахождение которых и соответствующих им функций, обычно называют задачей Штурма – Лиувилля.
Рассмотрим подробнее второе уравнение системы (17), переписав его в виде:
(18)
Перед нами однородное линейное уравнение второго порядка вида:
Последнее уравнение может быть приведено к канонической (или нормальной форме) , с помощью замены:
где
Слайд 14Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Применительно к уравнению (18) имеем замену:
где
и
Полагая, что y=mx, для функции u(y) из уравнения (18) следует:
или
Введя новую переменную:
и обозначая
для функции u(z) имеем:
(19)
Слайд 15Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Замечание: Уравнение (19), представляет собой приведенную форму вырожденного гипергеометрического уравнения,
которую обычно называют уравнением Уиттекера.
Уравнение (19), при m0=m, 2m≠±1,±2,… имеет следующие два линейно независимые решения:
и общее решение:
где – вырожденная гипергеометрическая функция, а C1 и C2 – некоторые постоянные, которые следует искать исходя из начальных условий (14) и условий нормировки (15).
Замечание: Однако применительно к рассматриваемой модели, для получения явного вида распределения f(x,t), мы будем искать общее решение уравнения (19) несколько другим методом.
Слайд 16Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Подстановка
приводит для функции к уравнению вида:
(20)
Уравнение (20) имеет решение, ограниченное на бесконечности и не имеющее сингулярности в нуле, лишь в том случае, когда величина
является целым числом, т.е. когда
где i = 0, 1, 2, … , что соответствует величинам:
Вывод: Решением уравнения (20), которое соответствует собственному значению является обобщенный многочлен Лагерра:
степени i и порядка (Θ-1).
Слайд 17Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Возвращаясь к искомой функции
с учетом системы (17), сделанных замен
и обозначений можно утверждать, что для предельного случая n=1, функции вида:
i = 0, 1, 2, …
являются частными решениями уравнения (13).
Тогда, общее решение этого уравнения для предельного случая n=1 может быть представлено в виде:
(21)
где Ci – постоянные, которые следует искать из начальных условий (14) и условий нормировки (15), используя свойства решений и функций, включая свойства специальных функций.
Слайд 18Вероятностно-статистическая модель гидродинамической стадии эволюции процесса классификации в гидроциклонах с
инжекцией
Мы получили в явном виде (21) искомое выражение для функции
распределения f(x,t), которое предоставляет возможность найти зависимость вида распределения стоксовских безынерционных сферических частиц массы mч и диаметра dч в пространстве безразмерной координаты x=(R/R0)2 цилиндрической рабочей части классификатора радиуса R0 от времени пребывания t в ней и конструктивных параметров аппарата, с учетом расходных характеристик и свойств разделяемой дисперсной системы.
При этом к конструктивным параметрам можно отнести величины – γ0, L, R0, kγ, kin, Sвх, к расходным характеристикам величины – Q и Qin, к свойствам разделяемой дисперсной системы – μ0, ρч и ρс.
В свою очередь эти величины образуют некоторые комплексы (постоянные), которые можно условно подразделить на: внешние, внутренние и комбинированные. Условно, к внешним комплексам можно отнести величины – Сч, D, С∑, с, А0, Аin, А∑, k, к внутренним – величины B и b, к комбинированным – m и Θ.
Использование выражения (21) не является тривиальным и в инженерной практике может вызывать большие затруднения. Это обстоятельство делает необходимым введение дополнительных обоснованных допущений, которые позволили бы существенно упростить последующие исследования и расчеты.

Слайд 19Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
С целью упрощения вида полученной функции распределения f(x,t),
обратимся к рассмотрению сомножителей:
входящих в состав выражения (21).
Влияние аналогичных сомножителей , но при K=const, на вид функций распределения, для схожих диффузионных моделей процессов измельчения, фильтрования, седиментации и т.п., описываемых с помощью обобщенных многочленов Лагерра, исследовалось многими авторами.
При этом было установлено, что с точностью, необходимой для инженерных расчетов, при , вид функций распределения f(x,t) не зависит от времени t и практически не отличается от предельного стационарного распределения f∞(x), т.е. имеет место:
(22)
Вывод: для моментов времени вид распределения f(x,t) не зависит от времени и справедливо f(x,t)= f∞(x).
Слайд 20Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Среднее время пребывания частицы в цилиндрической рабочей части
классификатора можно оценить с помощью выражения:
(23)
где f(t) – функция распределения по времени пребывания частиц в рабочей части классификатора; – объем цилиндрической рабочей части гидроциклона; (Q+Qin) – полный расход разделяемой дисперсной системы.
Замечание: Для гидроциклонов, имеющих практическое значение, величину согласно (23) можно оценить на уровне, не превышающем нескольких секунд ( ~ 0,1…10 с).
Величину можно оценить по порядку на уровне Ki ~ 103…108 с-1 т.к. её составляют сомножители k2/b и (Θ+i)/(Θ+2i)2, первый из которых, можно оценить на уровне ~ 103…108с-1, а второй на уровне не превышающем нескольких единиц.
Вывод: величины имеют порядок на уровне не более t∞ ~ 10-2 и неравенство >>t∞ – выполняется для любых практически значимых классификаторов.
Слайд 21Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Вывод: Применение предельного стационарного распределения f∞(x) для определения
изменения характеристик разделения гидроциклонов является вполне обоснованным и подлежит экспериментальной проверке.
В свою очередь, это позволяет существенно упростить решение (21), представив его в виде аналитического выражения (гамма-распределения) для предельного случая (22):
(24)
Принимая во внимание определение гамма-функции по Эйлеру, для всех действительных x > 0 справедливо:
что в свою очередь, с учетом условия нормировки (15), позволяет определить постоянную C0 в выражении (24), как:
(25)
Действительно, применяя операцию к обеим частям выражения (24) имеем:
и с учетом (15) получаем (25).
Слайд 22Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Из (24) и (25) следует, что в процессе
классификации через некоторое время, после ввода разделяемой дисперсной системы в аппарат, устанавливается предельное стационарное распределение f∞(x), вид которого не зависит от начального распределения f(x,0)=f0(x).
Замечание: Рассматриваемая система в процессе своей эволюции через некоторое время t∞, полностью "забывает" свое прошлое, что является характерной чертой случайных марковских процессов, т.е. систем не обладающих "памятью".
При этом слева от моды (при x→0 ) предельное стационарное распределение ведет себя, как степенная функция ~xΘ, а справа от моды (при x→∞), как экспоненциальная функция ~ e-mx.
Для нахождения абсциссы xm, максимума плотности распределения, называемого модой, приравниваем нулю первую производную функции
плотности распределения (24),
Полученное выражение показывает, что распределение (24) является одномодальным, с абсциссой моды:
(26)
Слайд 23Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
С практической точки зрения соотношение (26) является весьма
полезным, поскольку в пространстве безразмерной координаты x, не только устанавливает взаимосвязь между коэффициентами c и k, характеризующими интенсивность центробежных сил и классификационного воздействия, но и наделяет их отношение наглядным физическим смыслом.
Вывод: Положение абсциссы моды xm распределения (24) в пространстве безразмерной координаты x не зависит от интенсивности случайных возмущений b.
Обратимся к рассмотрению уравнения (13), оно также допускает весьма наглядную интерпретацию. Его можно записать в виде, аналогичном виду обычного уравнения неразрывности:
где – плотность соответствующего потока.
Для стационарного состояния и J(x)=J∞=const, что позволяет записать:
(27)
Слайд 24Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Перед нами линейное уравнение первого порядка вида:
Последнее
уравнение имеет решение:
где
Тогда, решение уравнения (27) можно представить в виде:
где
а C0’, C1’ – некоторые постоянные.
В результате получаем:
(28)
Слайд 25Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
В наиболее общем виде процедура определения вида полученного
стационарного распределения f∞,n(x) сводится к нахождению представленного в выражении (28) интеграла, исследованию его свойств и определению постоянных.
Однако в рассматриваемом случае данная процедура может быть существенно упрощена. Для этого необходимо сопоставить распределение (28) с распределением (24), принимая во внимание, что последнее, является его предельным случаем (при n=1 ).
Очевидно, что в условиях статистического равновесия J∞=0 распределения (28) и (24) совпадают между собой. С физической точки зрения, для стационарного распределения, условие J∞=0 эквивалентно допущению, не только о постоянстве полного количества частиц данного размера в цилиндрической рабочей части гидроциклона, но и о постоянстве относительного количества частиц данного размера в каждом рассматриваемом интервале (x,x+dx).
В противном случае, при J∞≠0, в стационарных условиях происходит, либо непрерывное накопление частиц данного размера в цилиндрической рабочей части гидроциклона с последующей его забивкой, либо их непрерывное удаление, в количествах превышающих их поступление, приводящее к полному отсутствию частиц данного размера в цилиндрической рабочей части аппарата. И то и другое явно противоречит сделанным допущениям, законам сохранения и имеющимся экспериментальным данным.

Слайд 26Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Вывод: Для обеспечения стационарных условиях работы гидроциклона плотность
соответствующего потока частиц любого размера dч,j в пространстве x должна быть равна нулю J(x,t)=J(x)=J∞=0
Полагая, что J∞=0, α=2n/(n+1) и m’=m/α из (28) получаем:
(29)
Применяя операцию к обеим частям выражения (29), с учетом (15), имеем:
Далее, используя определение гамма-функции по Эйлеру, находим:
(30)
Слайд 27Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Выражения (29) и (30) полностью определяют функцию стационарного
распределения f∞,n(x) в пространстве безразмерных координат x, при n [0,5,1], в зависимости от коэффициентов k, c и b, характеризующих интенсивность классификационного воздействия, центробежных сил и случайных возмущений, соответственно.
При этом определяющими величинами по-прежнему являются не сами коэффициенты k, c и b, а относительные величины (комбинированные комплексы) и , характеризующие соответственно относительные интенсивности классификационного воздействия и центробежных сил по сравнению с интенсивностью случайных возмущений.
Возникает естественный вопрос о правомерности использования предельного стационарного распределения f∞,n(x) при оценке изменения характеристик разделения циклонных классификаторов, ведь аналитическое решение уравнения (13) осуществлялось лишь для частного случая , а оценок того, что этот случай действительно является предельным и в части временных оценок не проводилось.

Слайд 28Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Обратимся к рассмотрению этого вопроса, начиная с качественного
рассмотрения стадии ввода разделяемой дисперсной системы в цилиндрическую рабочую часть классификатора. На этой стадии, в начальный момент времени частицы дисперсной фазы сосредоточены на конце входного патрубка и имеют координату абсциссы моды x0=1.
Далее, в процессе ввода разделяемой дисперсной системы, независимо от величины n [0,5, 1], координата моды меняет свое положение на величину sn=|x-x0| .
Аналогичный процесс происходит и на гидродинамической стадии эволюции процесса классификации до тех пор, пока абсцисса моды не достигнет своего стационарного значения xm,n и будет выполняться sn=smax,n=|xm,n-x0|, для n [0,5,1].
Для нахождения абсциссы xm,n, максимума плотности стационарного распределения f∞,n(x), приравниваем нулю первую производную функции плотности распределения (29):
Полученное выражение показывает, что распределение (29), также как распределение (24), является одномодальным, но с абсциссой моды:
(31)

Слайд 29Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Соотношение (31) не только устанавливает взаимосвязь между коэффициентами
c и k, характеризующими интенсивность центробежных сил и классификационного воздействия, но и показывает, что положение абсциссы моды xm,n, также как положение абсциссы моды xm распределения (24), в пространстве безразмерной координаты x не зависит от интенсивности случайных возмущений b.
При этом, для n [0,5; 1), α [0,66; 1) и 1/α [1,5; 1), выполняется xm,n < xm при c/k < 1 и xm,n ≥ xm при c/k ≥ 1. Соответственно имеет место неравенство smax,n >smax,1 при n≠1.
Иначе говоря, система проходит минимальный эволюционный путь в пространстве безразмерной координаты x при n=1. Поскольку величины абсцисс моды xm и xm,n, не зависят от интенсивности случайных возмущений b можно считать, что время изменения положения абсцисс моды обратно пропорционально средней скоростью соответствующего процесса
. и
При этом для x0 →xm и x0 →xm,n, независимо от положения абсциссы моды, при прочих равных условиях, выполняется |W’n| ≥ |W’|. Указанное обстоятельство позволяет предположить, что после ввода разделяемой дисперсной системы в гидроциклон, промежутки времени за которые устанавливаются стационарные распределения f∞(x) и f∞,n(x) имеют один порядок.
Вывод: Выполненные выше оценки для распределения f∞(x) могут быть распространены и на распределение f∞,n(x).

Слайд 30Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Представленные оценки позволяют сделать вывод, что применение предельного
стационарного распределения f∞,n(x) для определения характеристик разделения циклонных классификаторов является вполне обоснованным и подлежит экспериментальной проверке.
Следует особо подчеркнуть, что в общем случае коэффициенты W’(S) и B’(S) в уравнении ФПК выражаются через усредненные характеристики процесса и в этом смысле их вычисление может быть сведено к чисто механической задаче.
Однако, при наличии в процессе классификации состояния статистического равновесия, фактически нет необходимости в раздельном вычислении коэффициентов W’(S) и B’(S) в кинетическом уравнении (11).
В частном случае эти коэффициенты могут быть выражены друг через друга из условия обращения в ноль плотности соответствующего потока в состоянии статистического равновесия.
В нашем случае эта задача при необходимости может быть решена путем подстановки того или иного предельного стационарного (равновесного) распределения в уравнение J∞=0.
С целью определения трансформации предельных стационарных распределений в зависимости от изменения диаметра частиц и радиуса цилиндрической рабочей части гидроциклона R перейдем к новой безразмерной переменной r=R/R0.

Слайд 31Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Как уже отмечалось ранее, уравнения того же типа,
что и кинетическое уравнение (11) будет справедливо и для функций распределения f по другим переменным, если только выполнены условия, лежащие в основе вывода уравнения ФПК – относительная малость изменения величин в элементарных актах взаимодействия и линейность по f интегрального оператора, выражающего изменение функции благодаря этим актам.
Применительно к рассматриваемой задаче, процедура нахождения стационарных функций распределения f по другим переменным может быть существенно упрощена, поскольку не требует составления и решения соответствующего кинетического уравнения.
Принимая во внимание известные соотношения f∞(x)dx=f∞(r)dr и f∞,n(x)dx=f∞,n(r)dr получаем:
что в свою очередь, с учетом обозначений (24), (25) и (29), (30), позволяет записать:
(32)
(33)
Слайд 32Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Выражения (32) и (33) полностью определяют функции стационарных
распределений f∞(r) и f∞,n(r) в пространстве безразмерных координат r, при n=1 и n [0,5; 1] соответственно, в зависимости от коэффициентов k, c и b, характеризующих интенсивность классификационного воздействия, центробежных сил и случайных возмущений.
При этом определяющими величинами по-прежнему являются не сами коэффициенты k, c и b, а относительные величины (комбинированные комплексы) , и , характеризующие соответственно относительные интенсивности классификационного воздействия и центробежных сил по сравнению с интенсивностью случайных возмущений.
Для нахождения абсцисс xm(r) и xm,n(r), максимума плотности стационарных распределений f∞(r) и f∞,n(r), приравниваем нулю первую производную функций плотности распределения (32) и (33), в результате получаем:
Слайд 33Исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в
гидроциклонах
с инжекцией
Полученные выражения показывают, что распределения (32) и (33)
является одномодальными, с абсциссой моды:
(34) (35) соответственно.
Выражения (34) и (35) показывают, что положения абсцисс моды в пространстве безразмерной координаты r уже зависит не только от относительной интенсивности центробежных сил по сравнению с классификационным воздействием, но и от интенсивности случайных возмущений b, точнее, от относительной интенсивности случайных возмущений по сравнению с интенсивностью классификационного воздействия.
При этом вопрос об определяющем влиянии классификационного воздействия и случайных возмущений остается открытым и требует, как экспериментальной, так и расчетной проверки с привлечением соответствующего программного обеспечения.
Представленное исследование асимптотических свойств модели гидродинамической стадии эволюции процесса классификации в гидроциклонах позволяет перейти к решению важной прикладной задачи – определению характеристик разделения циклонных классификаторов.
Замечание: Без решения данной задачи практическая ценность данной модели будет резко сокращена, более того однозначное и корректное сопоставление полученных результаты исследований окажется попросту невозможным.

Слайд 34Определение характеристик разделения гидроциклонов
Распределение (29) остается справедливым для любой j-ой
фракции разделяемой дисперсной системы, что позволяет записать: f∞,n,j(x)=f∞,n(x,dч,j)=f∞,n(x,j).
Тогда, сепарационная
функция – , которая показывает долю частиц любой j-ой фракции, уловленных в классификаторе и поступающих в нижний выход может быть определена в виде:
(36)
Соответственно сепарационная функция – , которая показывает долю частиц любой j-ой фракции, прошедших классификатор и поступающих на верхний выход может быть определена в виде:
(37)
При этом выражения (36) и (37) связаны очевидным соотношением .
Вывод: Это означает принятие допущения о том, что стенка цилиндрической рабочей части гидроциклона не оказывает непосредственного влияния на дальнейшее поведение частицы любой j-ой фракции и любая стоксовская безынерционная частица дисперсной фазы достигшая этой стенки, при , попадает в нижний выход. В противном случае она рано или поздно поступает на верхний выход.
Слайд 35Определение характеристик разделения гидроциклонов
Распределения (29), входящие в состав характеристик (36)
и (37), являются трехпараметрическим семейством кривых и формально (после некоторых
преобразований) совпадают с универсальными эмпирическими формулами Свенссона и Авдеева. Последние, описывают аналитические формы кривых распределения частиц продуктов измельчения.
Кроме того, Распределения (29) совпадают с аналитическим выражением Шифрина для описания числа капелек в облаках в зависимости от их размера. Однако в отличие от последних распределений, которые получены эмпирическим путем, распределения (29) могут быть отнесены к разряду теоретических формул, поскольку они были найдены исходя из вполне конкретных физических предпосылок.
Замечание: Все эти распределения можно рассматривать как обобщение большинства известных эмпирических и теоретических законов статистического распределения случайных величин. В частности, при определенных значениях параметров они могут быть преобразованы в нормальный закон Гаусса, в законы Максвелла, Пирсона и другие статистические закономерности, а также формулы Розина-Раммлера, Годена-Андреева-Шумана, Ромашова и т.п.
Внимание! Несмотря на разработанные механизмы применения (специальные таблицы и методы вычисления) трехпараметрических универсальных эмпирических формул, точность результатов которых, согласована с практическими нуждами, эти процедуры находят весьма ограниченную область применения из-за своей относительной сложности.

Слайд 36Определение характеристик разделения гидроциклонов
В результате поиск дополнительных обоснованных допущений, направленных
на упрощение вида распределения (29), путем сокращения количества определяющих параметров
следует признать, не только обоснованным, но и практически значимым.
Для решения этой задачи обратимся к рассмотрению одного важного свойства нормального распределения Гаусса – свойству статистического самоподобия (автомодельности), которое можно записать в следующем виде:
Эта запись означает, что для любых a > 0 и b > 0, две случайные величины xa,σ и bxσ имеют одинаковое распределение. Тогда, например, для характеристики разделения R’ можно записать:
При этом замена переменных в последнем интеграле сводит его к предыдущему. Аналогичным образом предыдущий интеграл может быть сведен к последнему.
Вывод: Изменение масштаба шкалы дисперсии (σ2→a2σ2) в распределении приводит к тому же самому результату, что и изменение масштаба аргумента (x→x/b) с коэффициентом самоподобия .
Слайд 37Определение характеристик разделения гидроциклонов
Поскольку для относительно крупных частиц разделяемой дисперсной
системы Θ>> 1 и распределения (24) и (29) стремятся к
δ-образным предельным распределениям, хорошей аппроксимацией которых является нормальный закон распределения, можно считать что здесь свойство автомодельности распределений (24) и (29) будет выполняться с необходимой точностью.
Для средних и относительно мелких частиц можно предположить, что это свойство будет выполняться лишь частично, только в интегральных оценках величины R’, т.к. здесь распределения (24) и (29) имеют координаты абсцисс моды в области x < 1, а при x > 1 обладают ниспадающими "хвостами" ~ и ~ примерно одинаковой площади. При этом примерное самоподобие распределений (24) и (29) для интегральных оценок величины можно записать в виде:
(38)
Вывод: Выражение (38) показывает, что изменение масштаба величины показателя степени (α→εα) для интегральных оценок величины R’ должно приводить к тому же самому результату, что и изменение масштаба величины постоянного коэффициента (b→βb).
Слайд 38Определение характеристик разделения гидроциклонов
Полагая εα=1, мы приходим к выводу, что
при соответствующем выборе βb, трехпараметрическое распределение (29), в части интегральных
оценок, может быть сведено к более простому двух параметрическому распределению (24). При этом отсутствие строго доказательства выполнения соотношения (38) требует его экспериментальной проверки.
Определяющее воздействие коэффициента b в рассматриваемой модели не заканчивается лишь возможностями масштабирования и учета интенсивности случайных составляющих классификационного процесса. Кроме всего прочего, на этот коэффициент возлагается также учет влияния стенок и коллективного поведения частиц в рабочей части аппарата и ряда других факторов. К последним, в первую очередь следует отнести гидродинамические особенности потоков в аппарате и физико-химические свойства разделяемой дисперсной системы.
Очевидно, что детальное теоретическое исследование всех факторов, которые учитывает коэффициент b является самостоятельной междисциплинарной задачей, далеко выходящей за рамки данного курса. В связи с этим уже откажемся от использования "точных" законов – физических, физико-химических, гидродинамических, кинетических и т.п. Воспользуемся более простым подходом – феноменологическим, базирующимся на приближенных эвристических соображениях, которые следуют из этих "точных" законов.
Замечание: В прикладных технических исследованиях такой подход обладает, по меньшей мере, одним достоинством – ясностью в представлении и интерпретации полученных результатов.

Слайд 39Определение характеристик разделения гидроциклонов
Проводя аналогию с физическими процессами переноса, и
в частности с диффузионными процессами, можно утверждать, что в стационарном
состоянии осредненная "диффузионная" скорость движения частиц j-ой фракции v(dч,j)=v(j)=vj – может быть определена в пространстве через некоторый осредненный коэффициент диффузии частиц j-ой фракции B’(dч,j)=B’(j)=B’j – в виде:
(39)
где dч,j+Δl – эффективный радиус взаимодействия частиц j-ой фракции; Δl=const – изменение эффективного радиуса взаимодействия частиц j-ой фракции, за счет физико-химических явлений, например, за счет сольватных оболочек частиц; N(dч>dч,j) – число частиц в единице объема размер которых dч больше размеру частиц j-ой фракции.
Замечание: Выражение (39) учитывает не только изменение относительной скорости движения частиц и эффективного радиуса при взаимодействии частиц j-ой фракции, но и факт "рассеивания" частиц j-ой фракции на частицах более крупных фракциях.
С другой стороны скорость может быть определена в виде:
(40)
где B’∑ – некоторый постоянный коэффициент диффузии для частиц всех фракций; dч,j+l – эффективный радиус взаимодействия частиц j-ой фракции; l=const – постоянное осредненное изменение эффективного радиуса взаимодействия частиц j-ой фракции, при их "рассеивании" на частицах всех фракций; N∑ – полное число частиц всех фракций в единице объема.
Слайд 40Определение характеристик разделения гидроциклонов
Поскольку для частиц j-ой фракции b=bj ~
B’∑ и b∑ ~ B’∑ =const из (39) и (40)
получаем эмпирическую зависимость для коэффициента bj:
(41)
Величины b∑ ,l и Δl, входящие в выражение (41), можно считать постоянными для частиц любой j-ой фракции лишь для конкретной гидродинамической обстановки в классификаторе и по мере ее изменения они также будут изменяться. Это позволяет в первом приближении предположить, что b∑=b∑(Q,Qin), l=l(Q,Qin) и Δl= Δl(Q,Qin).
Отношение N∑/N(dч≥dч,j)=1/R’∑(dч,j) есть ничто иное, как величина, обратная остатку R’N(dч,j)=N(dч>dч,j)/N∑, представляющего собой долю числа частиц, диаметр которых больше некоторого фиксированного значения dч,j.
Для нахождения величины остатка R’N(dч,j) введем в рассмотрение функцию плотности распределения числа частиц φ(dч)=dD’(dч)/d(dч) в цилиндрической рабочей части гидроциклона по их диаметрам dч.
Тогда, с помощью "одночастичной" функции плотности распределения φ(dч), величину остатка R’N(dч,j) можно определить как:
(42)
Слайд 41Определение характеристик разделения гидроциклонов
Соответственно средний диаметр частиц , которые присутствуют
в цилиндрической рабочей части классификатора в стационарном режиме его работы,
может определен в виде:
(43)
Выражение (43) представляет собой одно из ограничений на вид функции φ(dч).
Вторым ограничением является обычное условие нормировки функции φ(dч)
(44)
Будем считать, что в состоянии статистического равновесия частицы дисперсной фазы идеально перемешаны в цилиндрической рабочей части классификатора и никаких других ограничений на вид функции φ(dч), помимо (43) и (44), не задано.
Воспользуемся известным принципом максимума энтропии:
Для решения задач отыскания условного экстремума функции обычно используют метод неопределенных множителей Лагранжа. Тогда, для состояния статистического равновесия в цилиндрической рабочей части классификатора, с учетом дополнительных условий (43) и (44), получаем:
(45)
где λ1, λ2 – неопределенные множители Лагранжа.
Слайд 42Определение характеристик разделения гидроциклонов
Выражение (45) для функции φ(dч) может строго
выведено при решении задач отыскания условного экстремума функционала энтропии:
с учетом дополнительных ограничений (43) и (44).
Замечание: В общем случае задачи такого рода решаются с помощью методов вариационного исчисления, которые в известном смысле представляют собой обобщения метода неопределенных множителей Лагранжа.
Здесь не будем приводить вывод явного вида функции распределения (45) с помощью того или иного метода, ограничимся лишь конечным результатом, который легко проверяется непосредственной подстановкой:
Это позволяет представить соотношение (45) в виде:
(46)
Подставляя правую часть формулы (46) в подынтегральное выражение в соотношении (42) и осуществляя интегрирование, получаем:
(47)
Соответственно, для N∑/N(dч≥dч,j)=1/R’∑(dч,j) с учетом (47) имеем:
(48)
Слайд 43Определение характеристик разделения гидроциклонов
Подстановка (48) в (41) окончательно дает:
(49)
Полученное феноменологическое
соотношение (49) раскрывает физический смысл коэффициента b∑, как коэффициента, который
характеризует интенсивность процессов турбулентной диффузии в пространстве x.
Действительно, для гомогенной системы l→0, Δl→0 и из (49) получаем bj →b∑.
Соответственно, значение коэффициента b∑, как и обычного коэффициента турбулентной диффузии, определяется в основном крупномасштабными пульсациями скорости и интенсивностью циркуляционных течений в цилиндрической рабочей части классификатора, т.е. гидродинамической обстановкой в аппарате. Это позволяет в первом приближении записать b∑=b∑(Q,Qin).
Кроме того, соотношение (49) показывает, что по мере увеличения диаметра dч,j стоксовских безынерционных частиц дисперсной фазы величина коэффициента bj сначала относительно быстро убывает (пропорционально 1/dч,j), а затем, после достижения минимальных значений, достаточно медленно возрастает (пропорционально edч,j). При этом можно предположить, что минимальные значения величины bj и величины R’1 будут достигаться примерно в одном диапазоне размеров частиц.

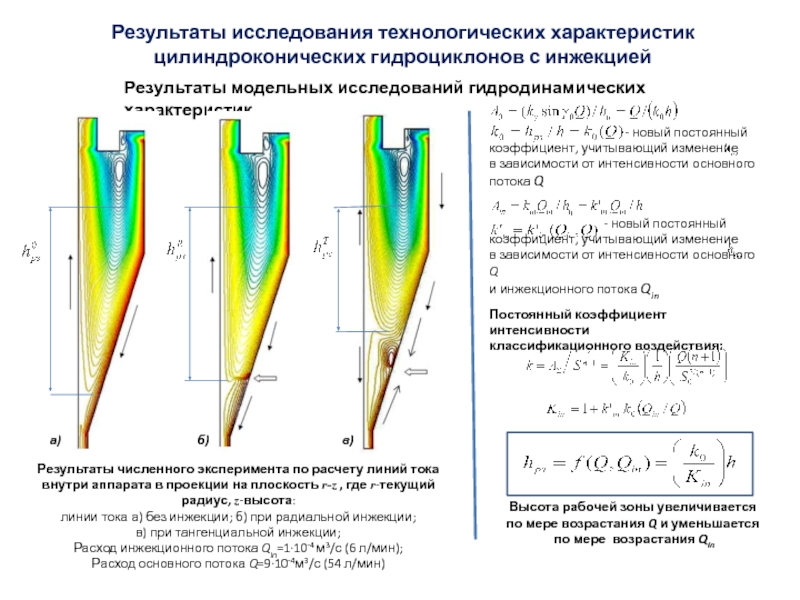
Слайд 44Результаты модельных исследований гидродинамических характеристик
Результаты исследования технологических характеристик цилиндроконических гидроциклонов
с инжекцией
Результаты численного эксперимента по расчету линий тока внутри
аппарата в проекции на плоскость r-z , где r-текущий радиус, z-высота:
линии тока а) без инжекции; б) при радиальной инжекции;
в) при тангенциальной инжекции;
Расход инжекционного потока Qin=1∙10-4 м3/с (6 л/мин);
Расход основного потока Q=9∙10-4м3/с (54 л/мин)
а) б) в)
- новый постоянный коэффициент, учитывающий изменение
в зависимости от интенсивности основного потока Q
- новый постоянный коэффициент, учитывающий изменение
в зависимости от интенсивности основного Q
и инжекционного потока Qin
Постоянный коэффициент интенсивности
классификационного воздействия:
Высота рабочей зоны увеличивается
по мере возрастания Q и уменьшается
по мере возрастания Qin
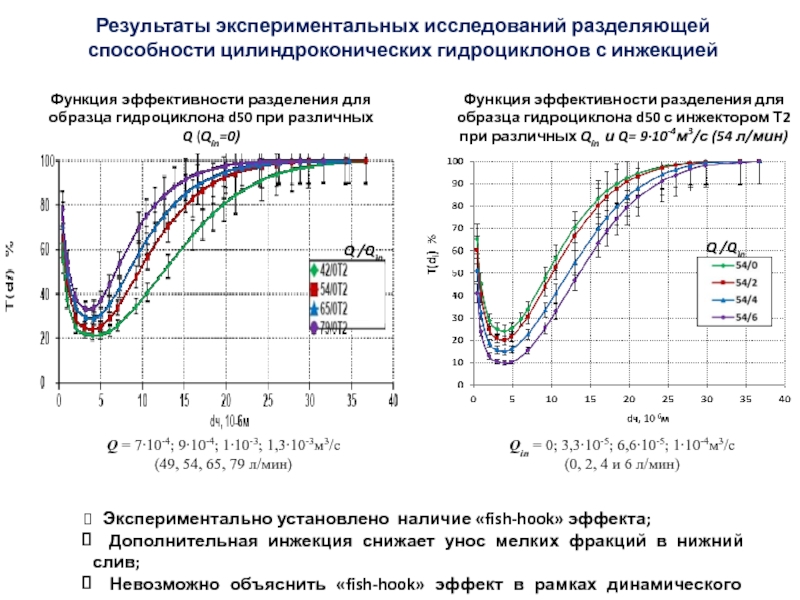
Слайд 45Функция эффективности разделения для образца гидроциклона d50 при различных Q
(Qin=0)
Экспериментально установлено наличие «fish-hook» эффекта;
Дополнительная инжекция снижает
унос мелких фракций в нижний слив;
Невозможно объяснить «fish-hook» эффект в рамках динамического подхода.
Результаты экспериментальных исследований разделяющей способности цилиндроконических гидроциклонов с инжекцией
Q = 7∙10-4; 9∙10-4; 1∙10-3; 1,3∙10-3м3/с
(49, 54, 65, 79 л/мин)
Qin = 0; 3,3∙10-5; 6,6∙10-5; 1∙10-4м3/с
(0, 2, 4 и 6 л/мин)
Функция эффективности разделения для образца гидроциклона d50 с инжектором Т2
при различных Qin и Q= 9∙10-4м3/с (54 л/мин)
Q /Qin
Q /Qin
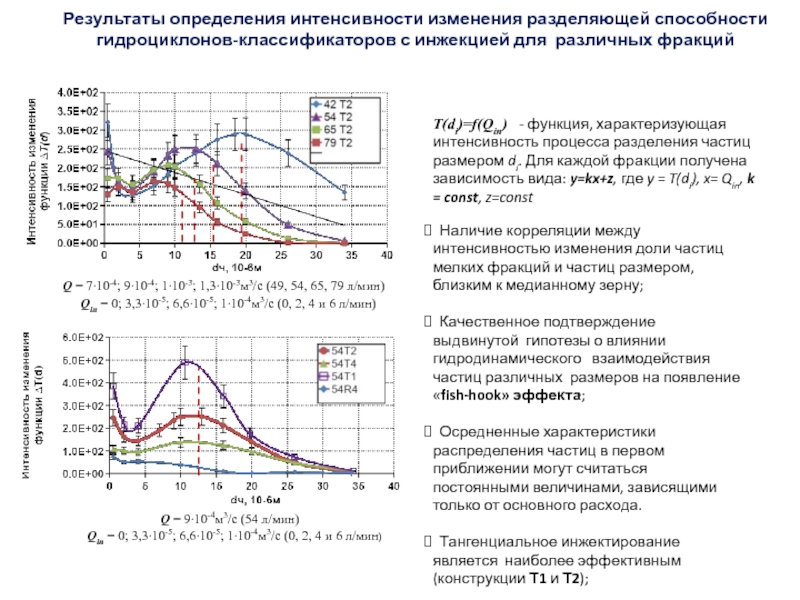
Слайд 46Результаты определения интенсивности изменения разделяющей способности
гидроциклонов-классификаторов с инжекцией для
различных фракций
Наличие корреляции между интенсивностью изменения доли частиц мелких
фракций и частиц размером, близким к медианному зерну;
Качественное подтверждение выдвинутой гипотезы о влиянии гидродинамического взаимодействия частиц различных размеров на появление «fish-hook» эффекта;
Осредненные характеристики распределения частиц в первом приближении могут считаться постоянными величинами, зависящими только от основного расхода.
Тангенциальное инжектирование является наиболее эффективным (конструкции Т1 и Т2);
T(di)=f(Qin) - функция, характеризующая интенсивность процесса разделения частиц размером di. Для каждой фракции получена зависимость вида: y=kx+z, где y = T(di), x= Qin, k = const, z=const
Q = 7∙10-4; 9∙10-4; 1∙10-3; 1,3∙10-3м3/с (49, 54, 65, 79 л/мин)
Qin = 0; 3,3∙10-5; 6,6∙10-5; 1∙10-4м3/с (0, 2, 4 и 6 л/мин)
Q = 9∙10-4м3/с (54 л/мин)
Qin = 0; 3,3∙10-5; 6,6∙10-5; 1∙10-4м3/с (0, 2, 4 и 6 л/мин)
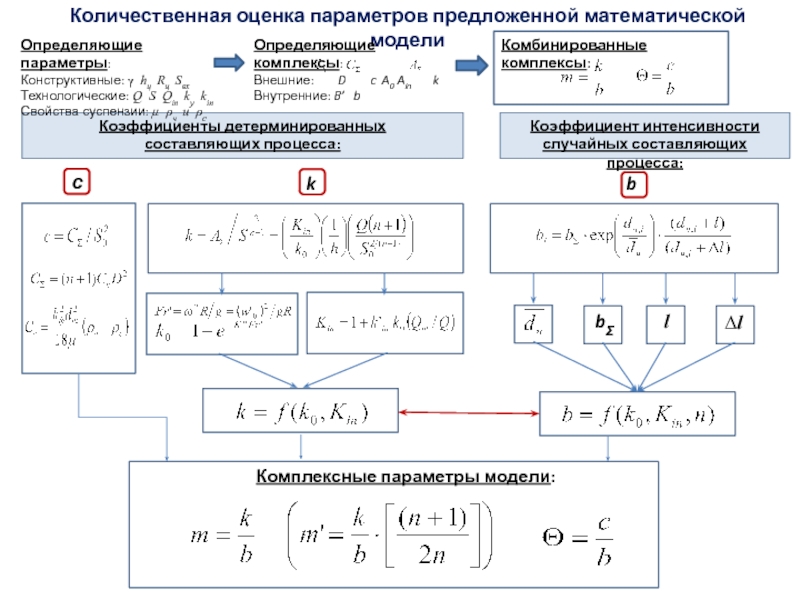
Слайд 47Количественная оценка параметров предложенной математической модели
Комплексные параметры модели:
∆l
b
bƩ
l
Коэффициенты
детерминированных
составляющих процесса:
Коэффициент интенсивности случайных составляющих процесса:
k
с
Определяющие параметры:
Конструктивные: γ hц
Rц Sвх
Технологические: Q S Qin ky kin
Свойства суспензии: µ ρч и ρс
Определяющие комплексы:
Внешние: D c A0 Ain k
Внутренние: B’ b
Комбинированные комплексы:
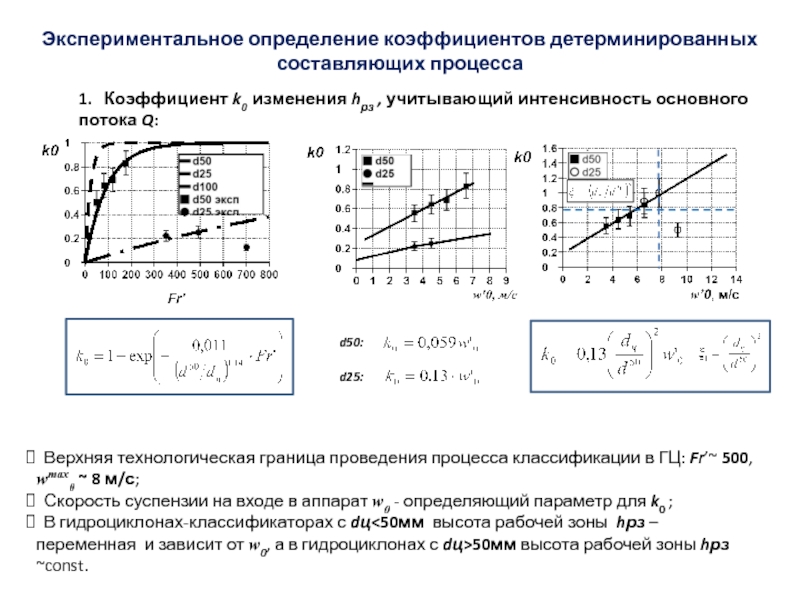
Слайд 48Экспериментальное определение коэффициентов детерминированных составляющих процесса
Верхняя технологическая граница проведения
процесса классификации в ГЦ: Fr’~ 500,
wmax0 ~ 8 м/с;
Скорость суспензии на входе в аппарат w0 - определяющий параметр для k0 ;
В гидроциклонах-классификаторах с dц<50мм высота рабочей зоны hрз – переменная и зависит от w0, а в гидроциклонах с dц>50мм высота рабочей зоны hрз ~const.
1. Коэффициент k0 изменения hрз , учитывающий интенсивность основного потока Q:
d50:
d25:
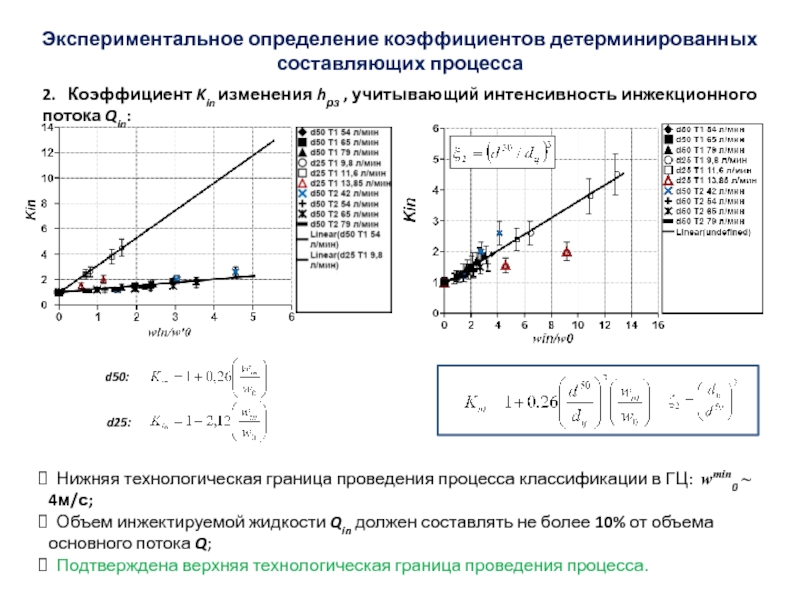
Слайд 492. Коэффициент Kin изменения hрз , учитывающий интенсивность инжекционного
потока Qin:
Экспериментальное определение коэффициентов детерминированных составляющих процесса
Нижняя технологическая граница
проведения процесса классификации в ГЦ: wmin0 ~ 4м/с;
Объем инжектируемой жидкости Qin должен составлять не более 10% от объема основного потока Q;
Подтверждена верхняя технологическая граница проведения процесса.
d50:
d25:
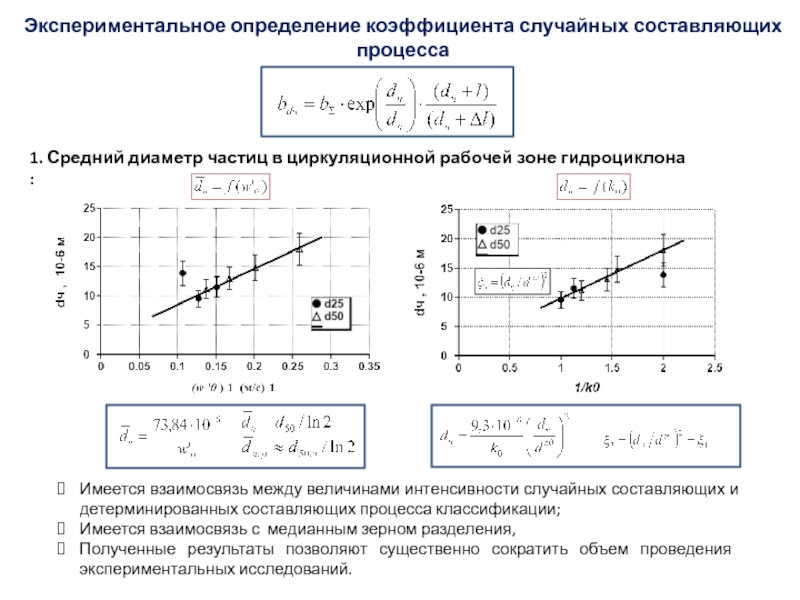
Слайд 501. Средний диаметр частиц в циркуляционной рабочей зоне гидроциклона :
Экспериментальное
определение коэффициента случайных составляющих процесса
Имеется взаимосвязь между величинами интенсивности случайных
составляющих и детерминированных составляющих процесса классификации;
Имеется взаимосвязь с медианным зерном разделения,
Полученные результаты позволяют существенно сократить объем проведения экспериментальных исследований.
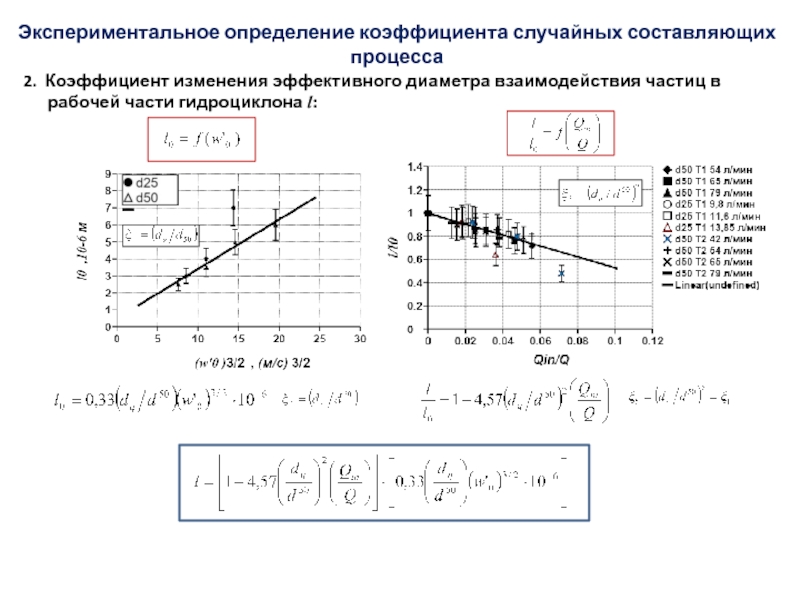
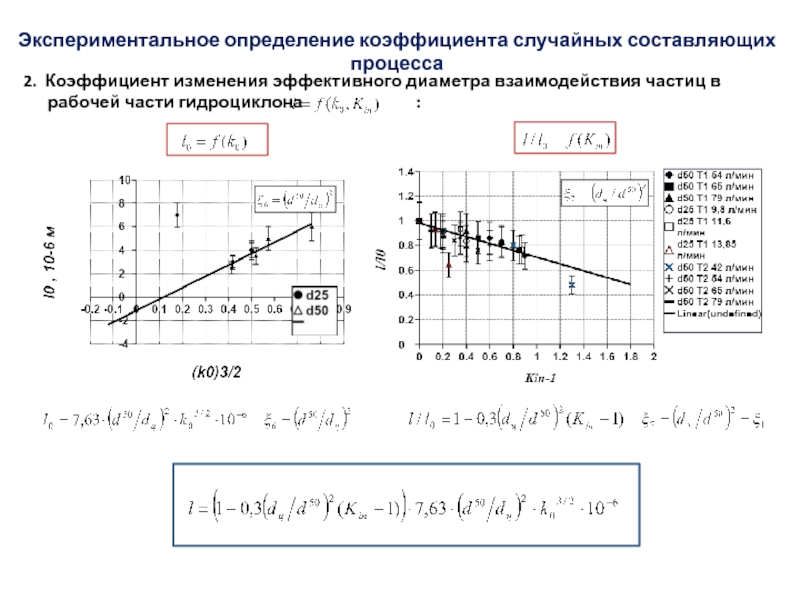
Слайд 512. Коэффициент изменения эффективного диаметра взаимодействия частиц в
рабочей части гидроциклона l:
Экспериментальное определение коэффициента случайных составляющих
процесса
Слайд 522. Коэффициент изменения эффективного диаметра взаимодействия частиц в
рабочей части гидроциклона
:
Экспериментальное определение коэффициента случайных составляющих процесса
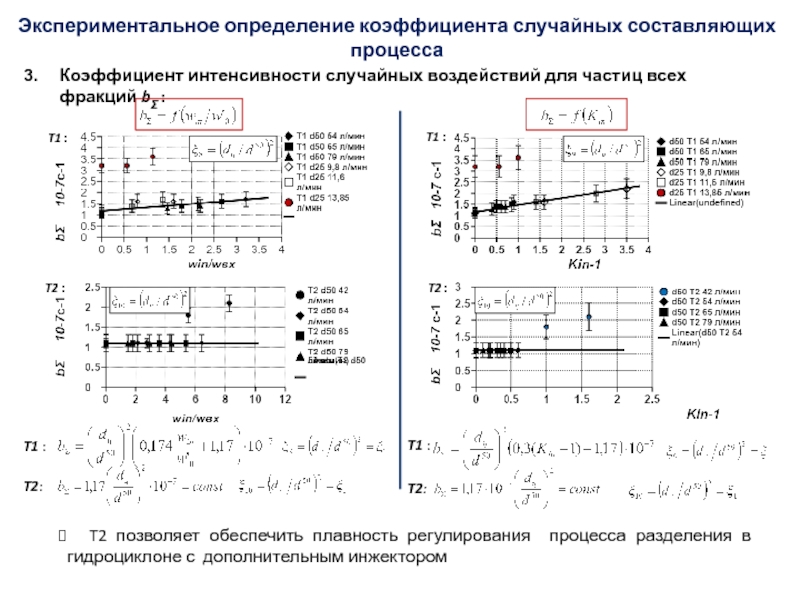
Слайд 53T2:
Коэффициент интенсивности случайных воздействий для частиц всех фракций bƩ :
T2 позволяет обеспечить плавность регулирования процесса разделения в гидроциклоне
с дополнительным инжектором
T1 :
Экспериментальное определение коэффициента случайных составляющих процесса
T1 :
T1 :
T2 :
T2 :
T2:
T1 :
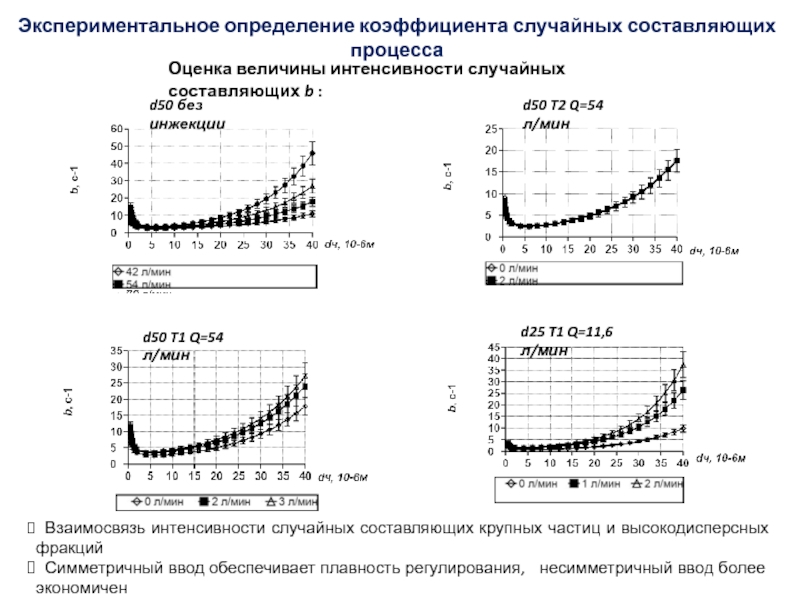
Слайд 54Оценка величины интенсивности случайных составляющих b :
d50 T2 Q=54 л/мин
d50
T1 Q=54 л/мин
d25 T1 Q=11,6 л/мин
Взаимосвязь интенсивности случайных составляющих
крупных частиц и высокодисперсных фракций
Симметричный ввод обеспечивает плавность регулирования, несимметричный ввод более экономичен
Экспериментальное определение коэффициента случайных составляющих процесса
d50 без инжекции
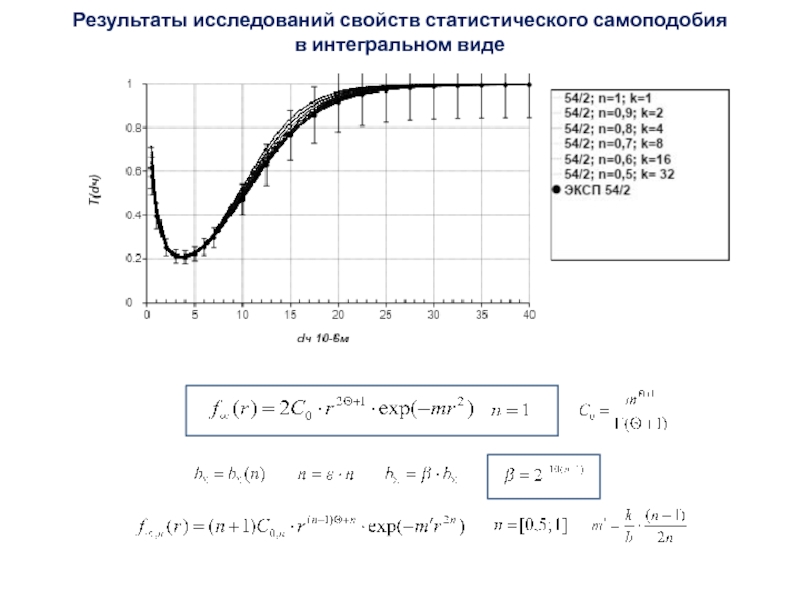
Слайд 55Результаты исследований свойств статистического самоподобия
в интегральном виде
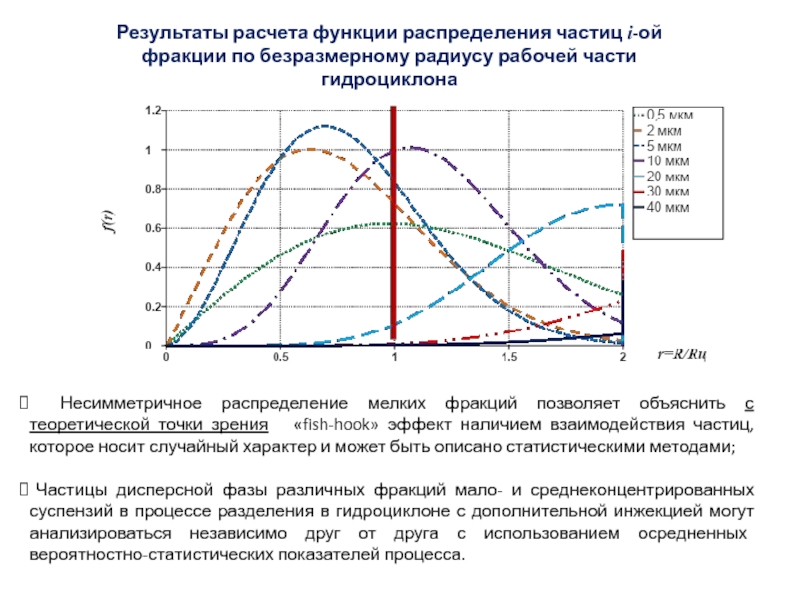
Слайд 56Результаты расчета функции распределения частиц i-ой фракции по безразмерному радиусу
рабочей части гидроциклона
Несимметричное распределение мелких фракций позволяет объяснить с
теоретической точки зрения «fish-hook» эффект наличием взаимодействия частиц, которое носит случайный характер и может быть описано статистическими методами;
Частицы дисперсной фазы различных фракций мало- и среднеконцентрированных суспензий в процессе разделения в гидроциклоне с дополнительной инжекцией могут анализироваться независимо друг от друга с использованием осредненных вероятностно-статистических показателей процесса.
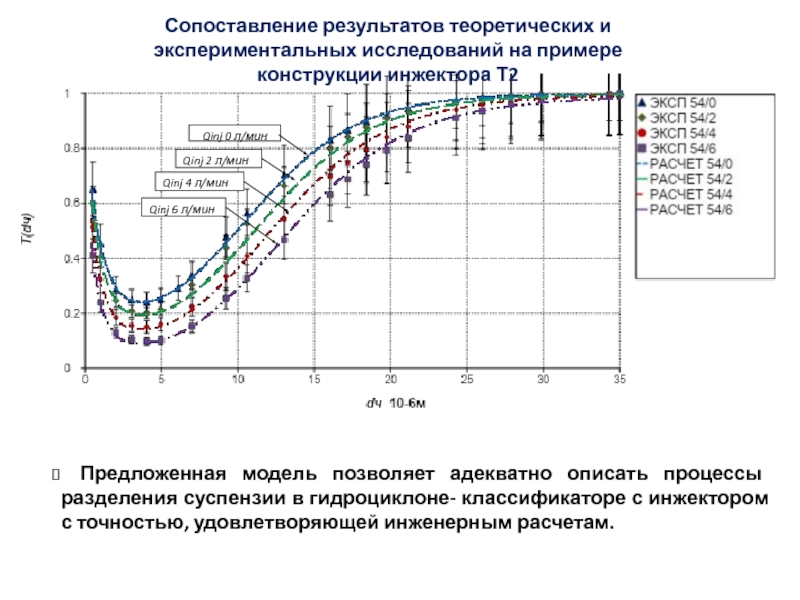
Слайд 57Сопоставление результатов теоретических и экспериментальных исследований на примере конструкции инжектора
Т2
Предложенная модель позволяет адекватно описать процессы разделения суспензии в
гидроциклоне- классификаторе с инжектором с точностью, удовлетворяющей инженерным расчетам.
Qinj 0 л/мин
Qinj 2 л/мин
Qinj 4 л/мин
Qinj 6 л/мин
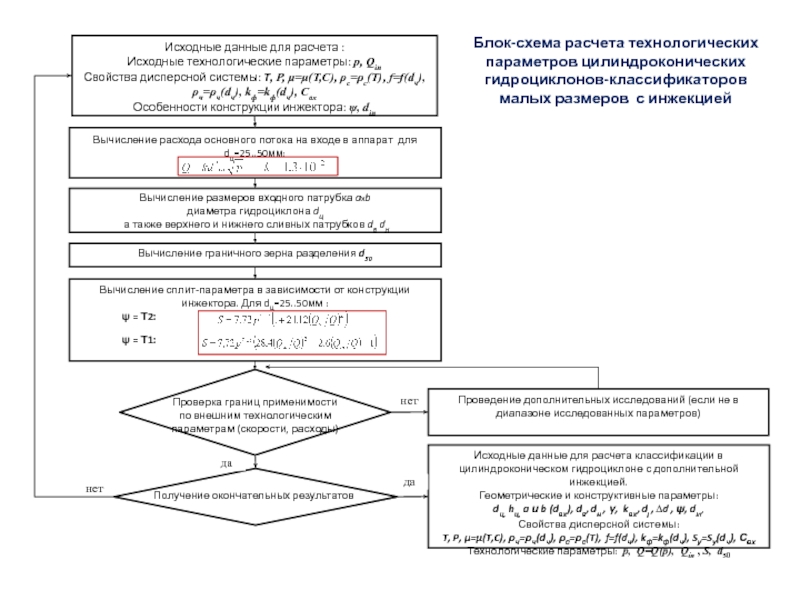
Слайд 58Исходные данные для расчета :
Исходные технологические параметры: p, Qin
Свойства дисперсной
системы: T, P, μ=μ(T,C), ρс=ρс(T), f=f(dч), ρч=ρч(dч), kф=kф(dч), Свх
Особенности конструкции
инжектора: ψ, din
Вычисление расхода основного потока на входе в аппарат для dц=25..50мм:
Вычисление размеров входного патрубка axb
диаметра гидроциклона dц
а также верхнего и нижнего сливных патрубков dв dн
Вычисление граничного зерна разделения d50
Вычисление сплит-параметра в зависимости от конструкции инжектора. Для dц=25..50мм :
ψ = Т2:
ψ = Т1:
Исходные данные для расчета классификации в цилиндроконическом гидроциклоне с дополнительной инжекцией.
Геометрические и конструктивные параметры:
dц, hц, a и b (dвх), dв, dн , γ, kвх, dj , ∆d , ψ, din,
Свойства дисперсной системы:
T, P, μ=μ(T,C), ρч=ρч(dч), ρс=ρс(T), f=f(dч), kф=kф(dч), Sу=Sу(dч), Свх
Технологические параметры: p, Q=Q(p), Qin , S, d50
Проведение дополнительных исследований (если не в диапазоне исследованных параметров)
Блок-схема расчета технологических параметров цилиндроконических гидроциклонов-классификаторов малых размеров с инжекцией
Получение окончательных результатов
Проверка границ применимости
по внешним технологическим параметрам (скорости, расходы)
да
нет
да
нет
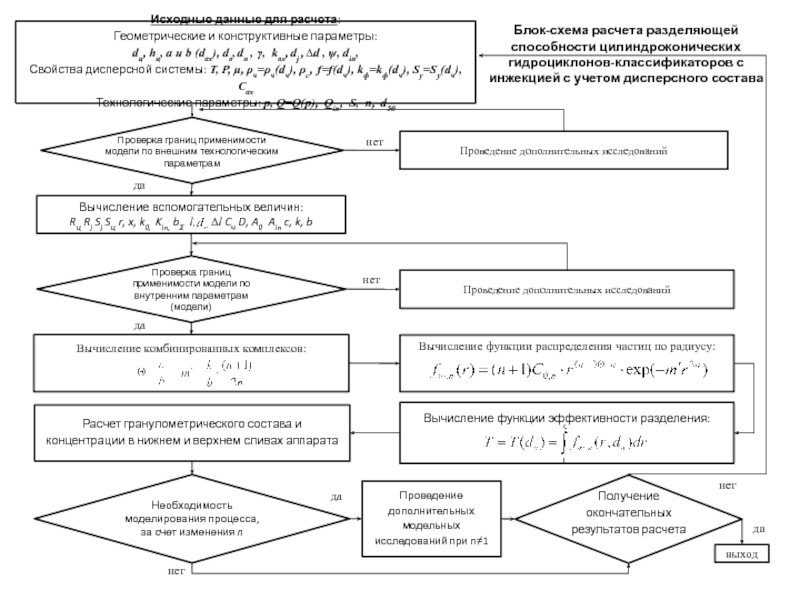
Слайд 59Исходные данные для расчета:
Геометрические и конструктивные параметры:
dц, hц, a и
b (dвх), dв, dн , γ, kвх, dj , ∆d
, ψ, din,
Свойства дисперсной системы: T, P, μ, ρч=ρч(dч), ρc, f=f(dч), kф=kф(dч), Sу=Sу(dч), Свх
Технологические параметры: p, Q=Q(p), Qin, S, n, d50
Проверка границ применимости модели по внутренним параметрам (модели)
Вычисление комбинированных комплексов:
Расчет гранулометрического состава и концентрации в нижнем и верхнем сливах аппарата
Необходимость моделирования процесса, за счет изменения n
Вычисление функции распределения частиц по радиусу:
Вычисление функции эффективности разделения:
Проведение дополнительных модельных исследований при n≠1
Блок-схема расчета разделяющей способности цилиндроконических гидроциклонов-классификаторов с инжекцией с учетом дисперсного состава
Проведение дополнительных исследований
Проведение дополнительных исследований
да
да
Вычисление вспомогательных величин:
Rц Rj Sj Sц r, x, k0, Kin, bƩ l, ∆l Cч D, A0 Ain c, k, b
выход
Получение окончательных результатов расчета
нет
да
нет
нет
нет
да
Проверка границ применимости
модели по внешним технологическим
параметрам
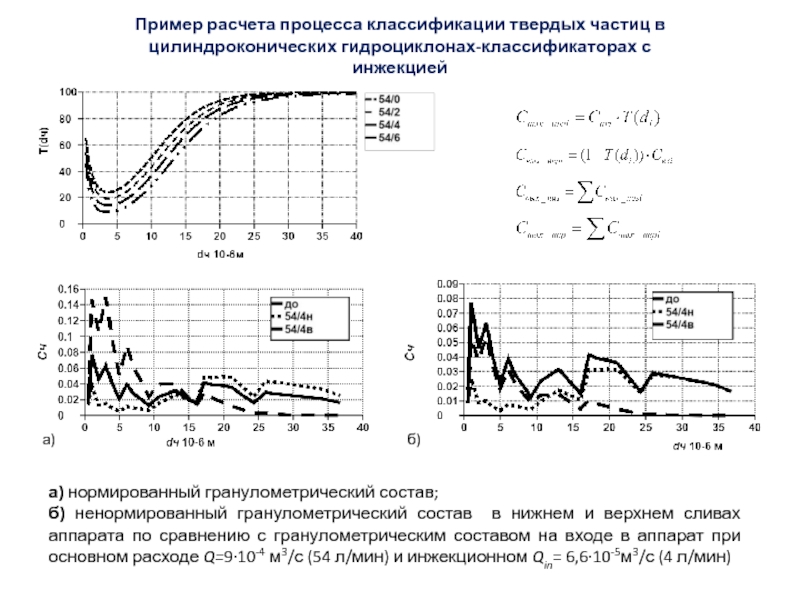
Слайд 60Пример расчета процесса классификации твердых частиц в цилиндроконических гидроциклонах-классификаторах с
инжекцией
а) нормированный гранулометрический состав;
б) ненормированный гранулометрический состав в нижнем
и верхнем сливах аппарата по сравнению с гранулометрическим составом на входе в аппарат при основном расходе Q=9∙10-4 м3/с (54 л/мин) и инжекционном Qin= 6,6∙10-5м3/с (4 л/мин)
а)
б)