Слайд 1ЛЕКЦИЯ 5
«ВИДЫ РАБОТ ПРИ ПОСТРОЕНИИ ТРИАНГУЛЯЦИИ»
Слайд 2 Последовательность видов работ при построении триангуляции.
Приведение измеренных направлений
к центрам пунктов.
Способы определения элементов приведения.
Предварительная обработка триангу-ляции.
Виды условных уравнений в триангуляции.
Допустимые размеры свободных членов условных уравнений.
Слайд 31. Последовательность видов работ при построении триангуляции.
При создании геодезических
сетей методом триангуляции выполняют следующие виды работ:
1. Составление технического проекта
сети по карте.
2. Рекогносцировка на местности вершин треугольников и выходных сторон.
3. Закладка центров и постройка триангуляционных знаков в вершинах треугольников.
Слайд 44.Определение значений длин и дирекционных углов выходных сторон.
5. Измерение углов
треугольников.
6.Обработка результатов измерений (предварительная обработка, уравнивание, вычисление координат и составление
каталогов пунктов).
При составлении проекта пользуются топографической картой. Намечают места размещения пунктов, рассчитывают высоты сигналов, делают предрасчет точности, определяют сметную стоимость работ и т.п.
Слайд 5Во время рекогносцировки при необхо-димости вносят изменения в проект.
Длины выходных
сторон в настоящее время измеряют электромагнитными дальномерами. Для измерения углов
в сетях 3, 4 кл. и сетях сгущения, в основном, применяют способ круговых приемов.
Обработку результатов измерений выполняют в настоящее время на ПЭВМ.
Слайд 62. Приведение измеренных направлений к центрам пунктов.
Геодезический знак стремятся строить
так, чтобы ось визирного цилиндра находилась на одной отвесной линии
с центром знака. Практически это условие не всегда выполняется. Вследствие этого при измерении углов прибор часто устанавливают не над центром пункта и наблюдают на визирные цели смежных пунктов, оси которых не совпадают с отвесными линиями центров пунктов.
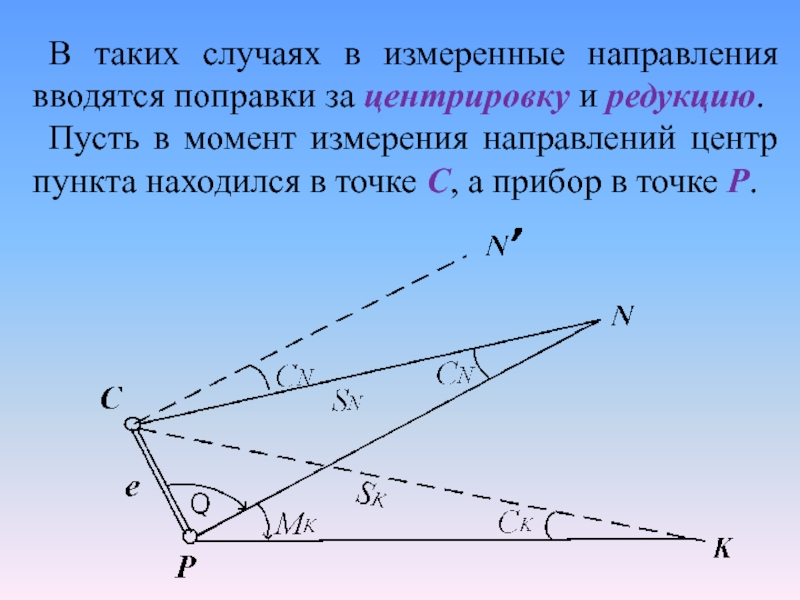
Слайд 7В таких случаях в измеренные направления вводятся поправки за центрировку
и редукцию.
Пусть в момент измерения направлений центр пункта находился
в точке С, а прибор в точке Р.
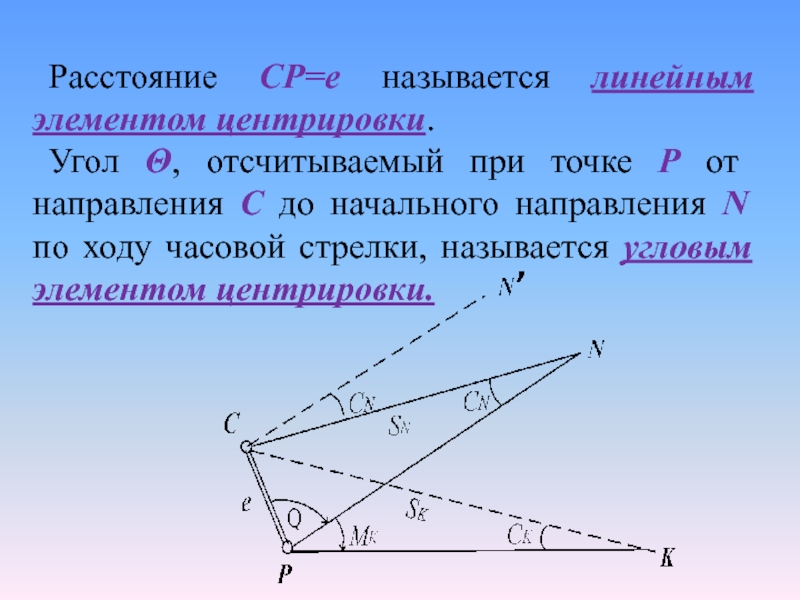
Слайд 8Расстояние CP=е называется линейным элементом центрировки.
Угол Θ, отсчитываемый при
точке Р от направления С до начального направления N по
ходу часовой стрелки, называется угловым элементом центрировки.
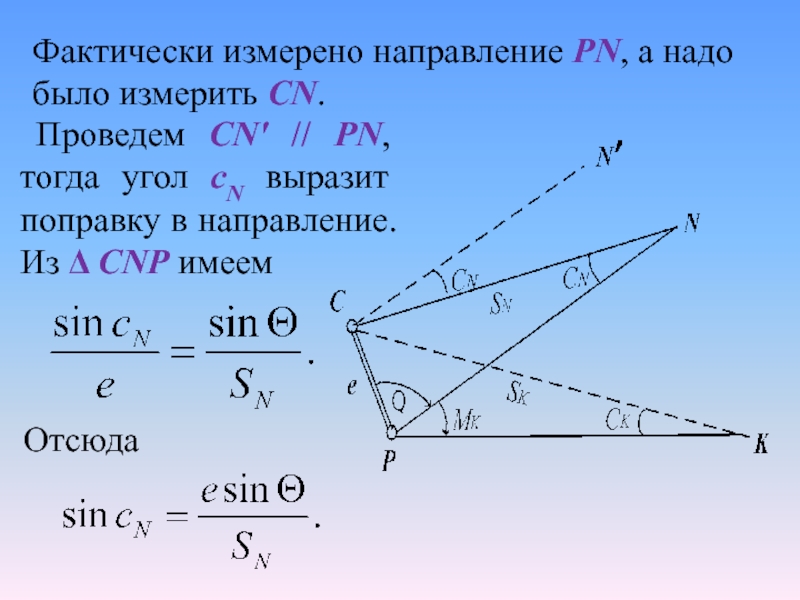
Слайд 9Проведем СN' // PN, тогда угол сN выразит поправку в
направление. Из Δ CNP имеем
Фактически измерено направление РN, а
надо было измерить СN.
Отсюда
Слайд 10По малости угла сN можно записать
Аналогично можно найти поправку в
любое направление. Например, поправка в направление на пункт К составит
где
МK – величина измеренного направления на пункт К.
Слайд 11В общем виде без индексов формулу для вычисления поправок за
центрировку можно записать так
Поправки за центрировку вводятся со своим знаком
в измеренные направления на данном пункте.
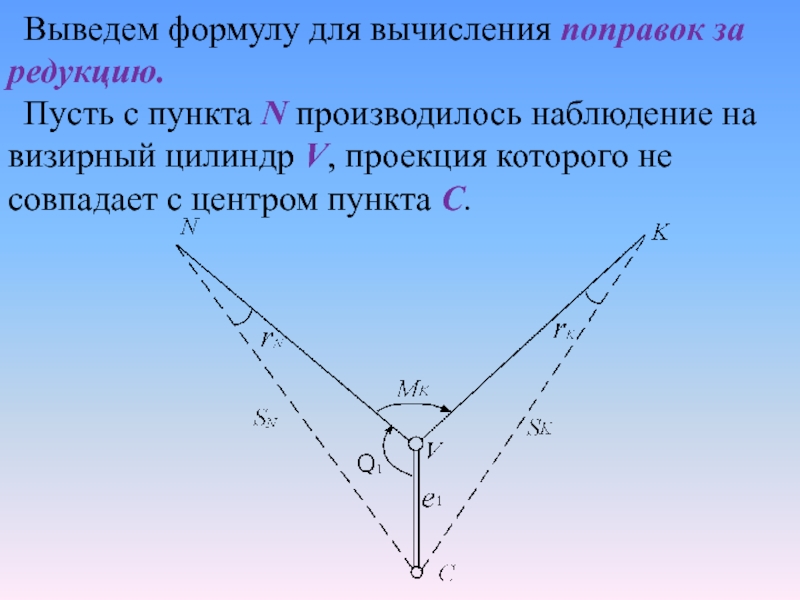
Слайд 12Выведем формулу для вычисления поправок за редукцию.
Пусть с пункта
N производилось наблюдение на визирный цилиндр V, проекция которого не
совпадает с центром пункта С.
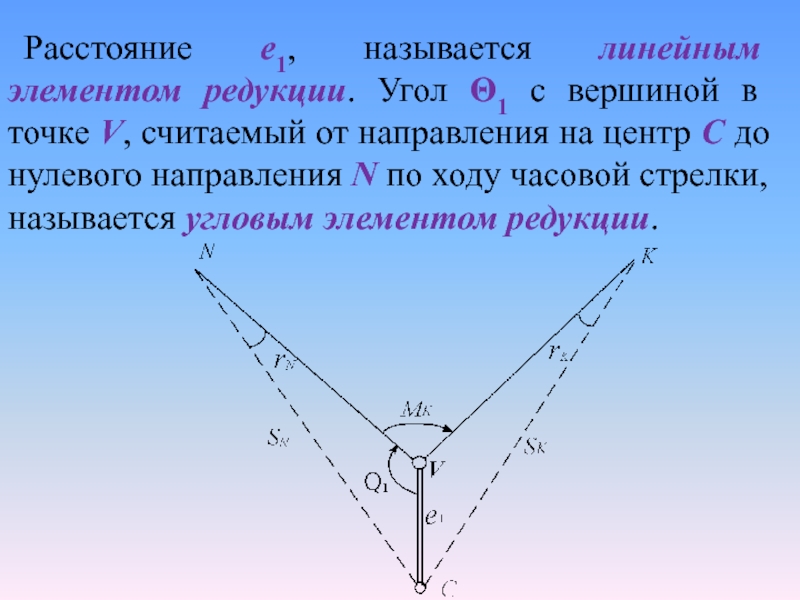
Слайд 13Расстояние e1, называется линейным элементом редукции. Угол Θ1 с вершиной
в точке V, считаемый от направления на центр С до
нулевого направления N по ходу часовой стрелки, называется угловым элементом редукции.
Слайд 14Из рис. видно, что в
направление NV нужно
ввести поправку
а в направление KV поправку
Слайд 15В общем виде формулу для вычисления поправок за редукцию можно
записать так
Поправки за редукцию вычисляются на данном пункте для
всех направлений, но вводятся со своим знаком в направления, измеренные на соседних пунктах.
Слайд 163. Способы определения элементов приведения.
Величины e, e1, Θ, Θ1 необходимые
для вычисления с и r называются элементами приведения. Для их
определения чаще всего применяют графический способ.
Над центром пункта устанавливают центрировочный столик, на который прикрепляют лист бумаги.
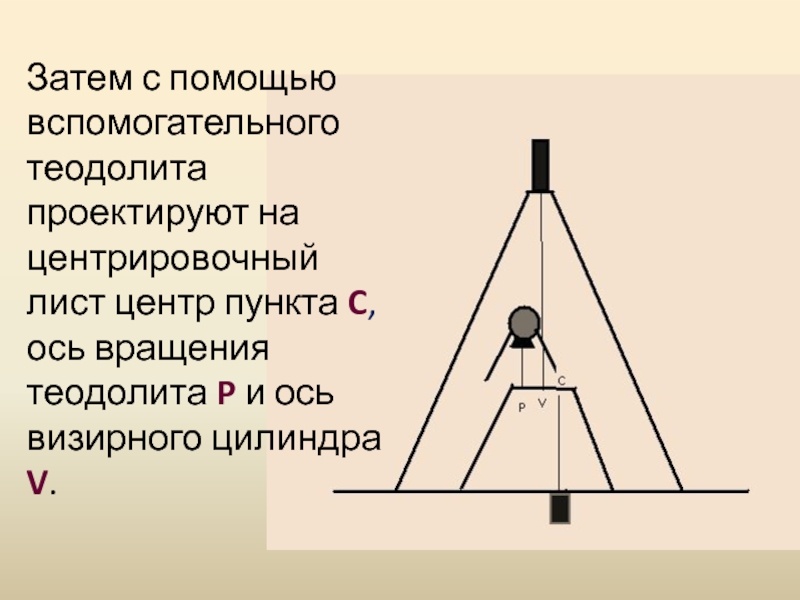
Слайд 17Затем с помощью вспомогательного теодолита проектируют на центрировочный лист центр
пункта C, ось вращения теодолита P и ось визирного цилиндра
V.
Слайд 18Проектирование выполняют при двух положениях круга с трех точек, расположенных
так, чтобы проектирующие плоскости пересекались под углом 1200. Стороны треугольников
погрешностей при проектировании точек С и Р не должны превышать 0,5 см, а для точки V – 1 см. Окончательное положение проекций точек С, Р и V намечают в центре треугольников погрешностей.
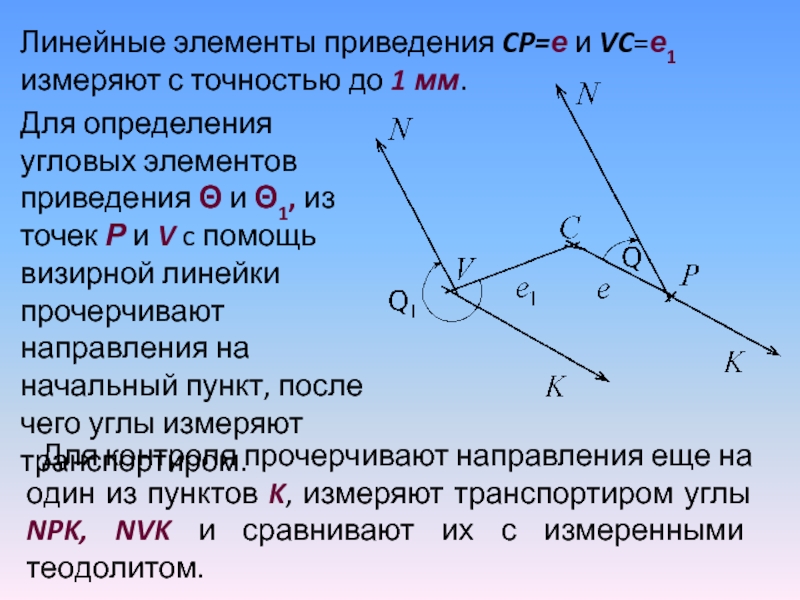
Слайд 19Для определения угловых элементов приведения Θ и Θ1, из точек
Р и V c помощь визирной линейки прочерчивают направления на
начальный пункт, после чего углы измеряют транспортиром.
Линейные элементы приведения CP=е и VC=е1 измеряют с точностью до 1 мм.
Для контроля прочерчивают направления еще на один из пунктов K, измеряют транспортиром углы NPK, NVK и сравнивают их с измеренными теодолитом.
Слайд 20Графический способ применяют в случаях, когда е и е1 небольшие.
Если е не вмещается на центрировочный лист, то его измеряют
непосредственно рулеткой, как расстояние между нитью отвеса, установленного над центром пункта, и нитью отвеса теодолита. Угол измеряют непосредственно теодолитом.
Слайд 214. Предварительная обработка триангуляция.
После выполнения полевых работ приступают к
предварительной обработке триангуляции:
1. Проверяют полевые журналы и центрировочные листы.
2.
Вычисляют средние значения направлений и составляют сводные ведомости измеренных величин.
3. Составляют схему сети с измеренными направлениями и углами.
Слайд 224. Выполняют предварительное решение треугольников.
5. Вычисляют поправки за центрировку
и редукцию.
6. Вычисляют приведенные к центрам направления.
7. Составляют
схему сети с приведенными направлениями.
Слайд 238. Вычисляют угловые невязки и проверяет их допустимость.
9. Делают
оценку точности угловых измерений по невязкам треуголь-ников.
10.Устанавливает допустимость невязок.
Слайд 245. Виды условных уравнений в триангуляции.
При построении триангуляции в
целях контроля и повышения точности кроме необходимых измеряют избыточные величины.
Например, в треугольниках измеряют все три угла, хотя для их решения необходимо только два.
Геодезические сети, имеющие только необходимые исходные данные, называются свободными.
Слайд 25Если сеть содержит избыточные исходные данные, то она несвободная. Каждое
избыточное измерение и избыточное исходное данное позволяют записать математическое соотношение
между измеренными величинами, т.е. условное уравнение.
При создании триангуляции возникают условия фигур, горизонтов, сумм, полюсов, сторон, дирекционных углов и координат.
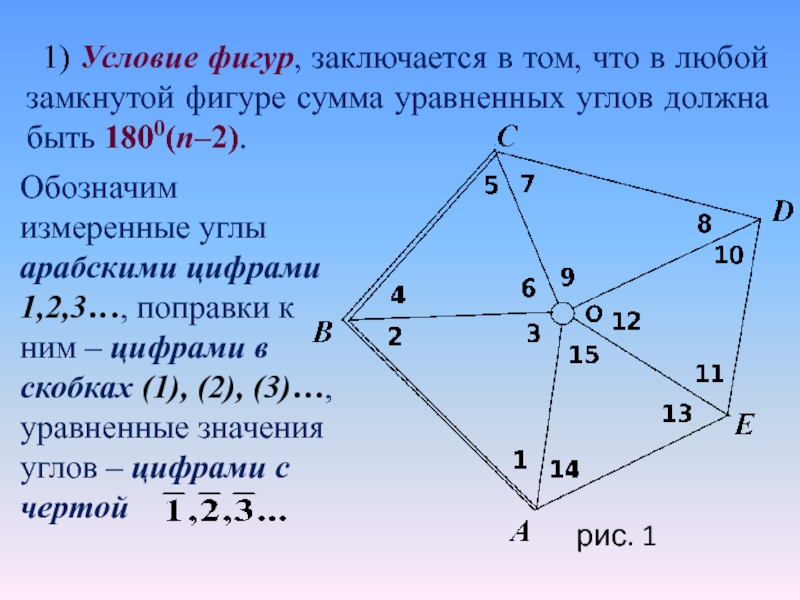
Слайд 261) Условие фигур, заключается в том, что в любой замкнутой
фигуре сумма уравненных углов должна быть 1800(n–2).
Обозначим измеренные углы
арабскими цифрами 1,2,3…, поправки к ним – цифрами в скобках (1), (2), (3)…, уравненные значения углов – цифрами с чертой
рис. 1
Слайд 27Тогда условие фигуры ABO запишется так
(1)
Учитывая, что
получим
1+(1)+2+(2)+3+(3)–1800 = 0.
Слайд 28Обозначим
1+2+3–1800 = w. (2)
Тогда
(1)+(2)+(3)+w = 0. (3)
Полученное
уравнение называется условным уравнением поправок.
Здесь w – свободный член
(невязка).
Слайд 292) Условие горизонта заключается в том, что сумма уравненных углов,
замыкающих горизонт на пункте, должна равняться 3600.
Применительно к рисунку имеем
Выразив уравненные углы через измеренные и поправки к ним, получим условное уравнение поправок
(3)+(6)+(9)+(12)+(15)+wГ = 0, (5)
где wГ = 3+6+9+12+15–3600 – свободный член (невязка).
рис. 1
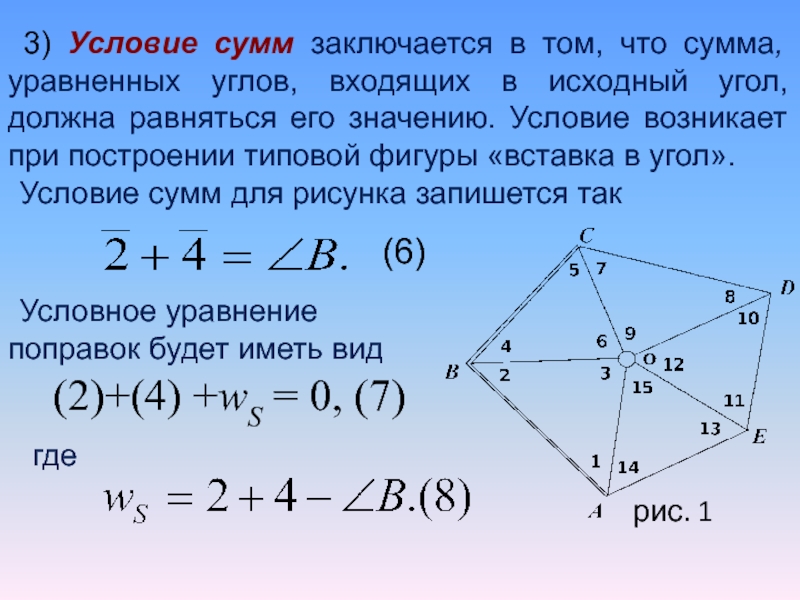
Слайд 303) Условие сумм заключается в том, что сумма, уравненных углов,
входящих в исходный угол, должна равняться его значению. Условие возникает
при построении типовой фигуры «вставка в угол».
Условие сумм для рисунка запишется так
(6)
Условное уравнение поправок будет иметь вид
(2)+(4) +wS = 0, (7)
где
рис. 1
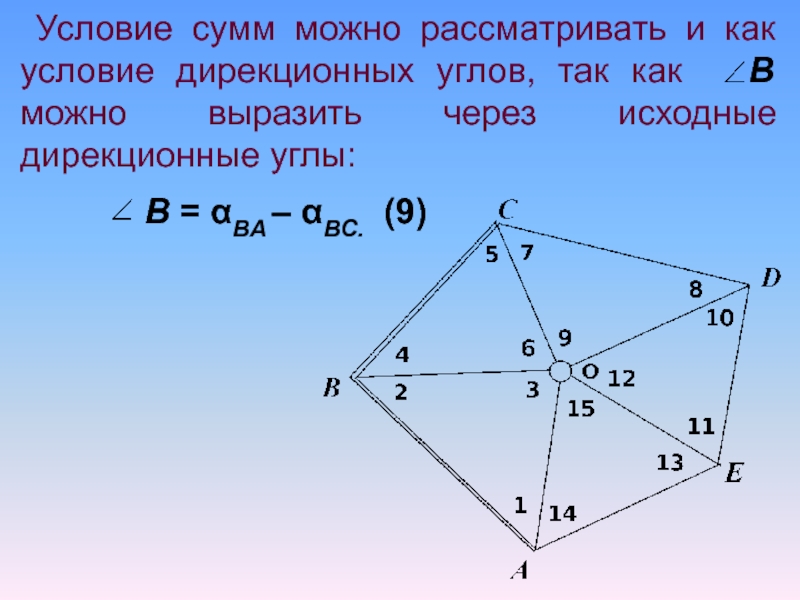
Слайд 324) Полюсное условие заключается в том, что длина одной и
той же стороны, вычисленная двумя независимыми путями по уравненным углам
должна иметь в обоих случаях одинаковое значение.
Возьмем в качестве исходной сторону ОА и вычислим дважды сторону ОD, решая треугольники по часовой стрелке и против часовой стрелки.
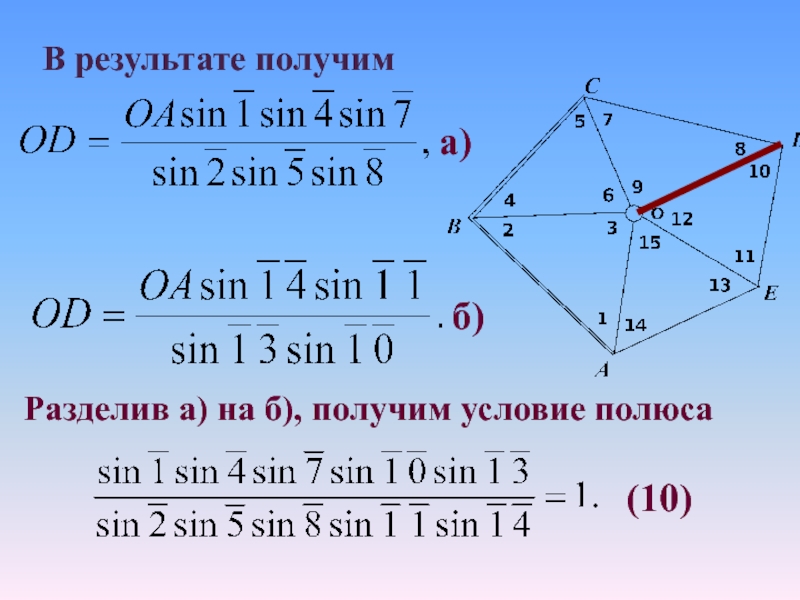
Слайд 33В результате получим
а)
б)
Разделив а) на б), получим условие полюса
(10)
Слайд 34Равенство (10) можно получить, решая треугольники по ходу часовой стрелки,
начиная от стороны OA и кончая стороной OA.
Все стороны имеют
общую точку О, называемую полюсом.
Для перехода к условным уравнениям поправок в уравнении (10) необходимо заменить уравненные углы измеренными с поправками и привести его к линейному виду, разложив в ряд Тейлора, ограничиваясь первыми степенями поправок.
Слайд 36Если второе слагаемое умножить и разделить на sin1, то его
с достаточной точностью можно заменить значением
. Аналогично мож-но преобразовать и другие слагаемые.
Введем следующие обозначения
Слайд 37Тогда полюсное условное уравнение поправок в угловой мере будет иметь
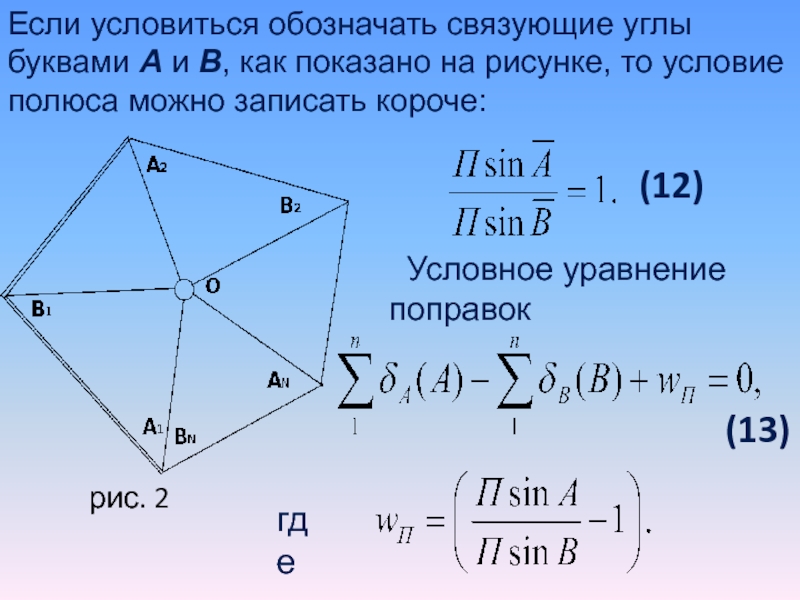
Слайд 38Если условиться обозначать связующие углы буквами А и В, как
показано на рисунке, то условие полюса можно записать короче:
(12)
Условное уравнение
поправок
(13)
где
рис. 2
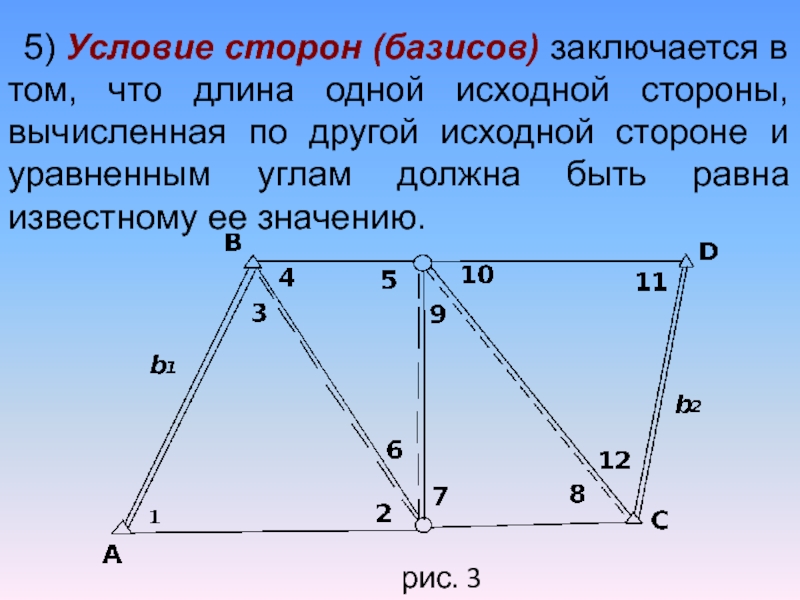
Слайд 395) Условие сторон (базисов) заключается в том, что длина одной
исходной стороны, вычисленная по другой исходной стороне и уравненным углам
должна быть равна известному ее значению.
рис. 3
Слайд 40Для данной цепи треугольников, заключенной между исходными сторонами b1 и
b2 можно записать
или в другом виде
(14)
Слайд 41Это равенство и будет выражать условие сторон. Оно аналогично (10).
Для перехода к условному уравнению поправок необходимо поступить так, как
в предыдущем случае. В результате получим
, (15)
Слайд 42где
(16)
Если связующие углы числителя обозначить через А, а в знаменателе
через В, то выражения (14), (15) и (16) можно записать
короче:
(17)
Слайд 43(18)
(19)
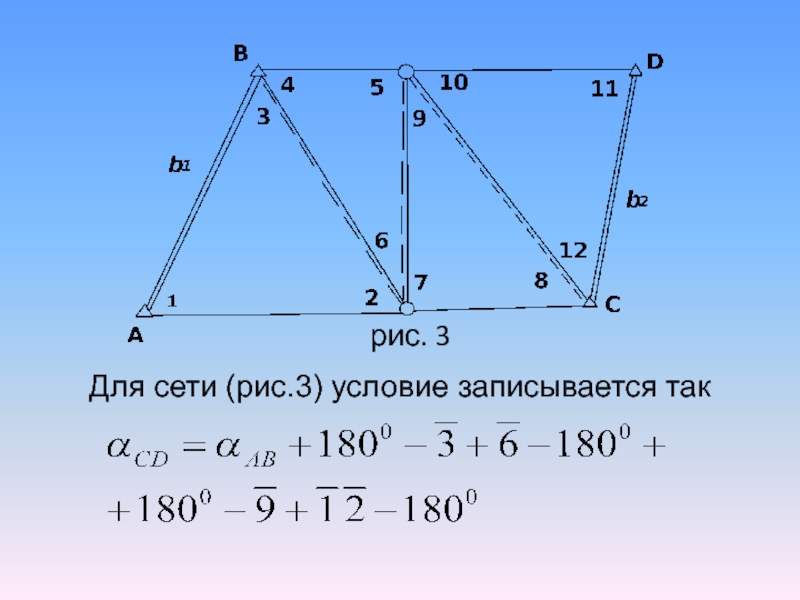
6) Условие дирекционных углов заключается в том, что дирекционный угол
одной исходной стороны, вычисленный по дирекционному углу другой исходной стороны
и уравненным углам должен быть равен известному его значению.
Слайд 44Для сети (рис.3) условие записывается так
рис. 3
Слайд 45Заменим уравненные углы измеренными c поправками
αAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0.
Обозначим
wα = αAB
–3 + 6 – 9 + 12 – αСD. (20)
Тогда
условное уравнение поправок примет вид:
–(3) + (6) – (9) + (12) + wα = 0. (21)






























![Виды работ при построении триангуляции Заменим уравненные углы измеренными c поправкамиαAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0. Обозначимwα = αAB –3 Заменим уравненные углы измеренными c поправкамиαAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0. Обозначимwα = αAB –3 + 6 – 9 + 12](/img/thumbs/f2c8b396bd114bc065238567afa501e4-800x.jpg)



















