Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ВИЗНАЧЕННЯ І КВАЛІФІКАЦІЯ ОСНОВНИХ РОЗРАХУНКОВИХ ПАРАМЕТРІВ В УМОВАХ ХАОТИЧНОЇ
Содержание
- 1. ВИЗНАЧЕННЯ І КВАЛІФІКАЦІЯ ОСНОВНИХ РОЗРАХУНКОВИХ ПАРАМЕТРІВ В УМОВАХ ХАОТИЧНОЇ
- 2. Вплив та види неоднорідностіБільшість методів визначення параметрів
- 3. Закономірна неоднорідність Закономірна неоднорідність пов'язана з
- 4. Хаотична неоднорідністьХаотична неоднорідність пов'язана з сингенетичними відмінностями
- 5. Відносність поняття фільтраційної неоднорідності
- 6. Характер неоднорідності (за М.В. Рацем)Неоднорідність вищого
- 7. ХАРАКТЕРИСТИКА ХАОТИЧНОЇ НЕОДНОРІДНОСТІ ЗА ДОПОМОГОЮ СТАТИСТИЧНИХ ОЦІНОК
- 8. Основні теоретичні положення Під хаотичною фільтраційною
- 9. Основні теоретичні положенняОбсяг інформації, укладений в результатах
- 10. Основні теоретичні положенняСтатистичні оцінки, одержувані на основі
- 11. Основні теоретичні положенняНа основі цього методу доведено,
- 12. Основні теоретичні положенняТакож важливим є питання про
- 13. Основні теоретичні положенняПри різних законах розподілу статистичні
- 14. Основні теоретичні положенняНеобхідно відзначити, що висновок щодо
- 15. КЛАСИФІКАЦІЯ ВОДОВМІСНИХ ПОРІД ЗА СТУПЕНЕМ ХАОТИЧНОЇ НЕОДНОРІДНОСТІ
- 16. Основні класифікаційні показникиОтримані статистичні оцінки можна використовувати
- 17. Стастичні оцінки показників фільтраційної неоднорідності Показники неоднорідності
- 18. Класифікація водовмісних порід за ступенем хаотичної неоднорідності
- 19. Вивчення мінливості коефіцієнта водопровідності (питомого дебіту) спирається
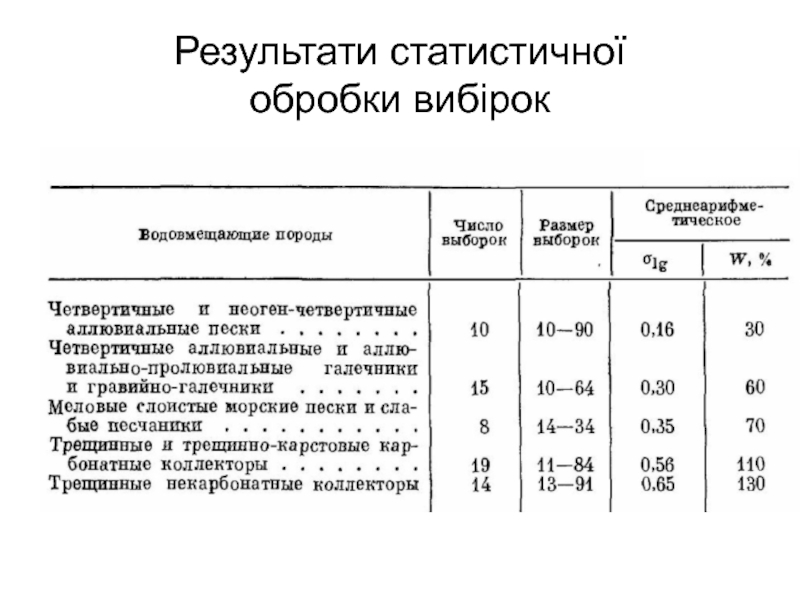
- 20. Результати статистичної обробки вибірок
- 21. Зв’язок нормального закону з
- 22. Відповідності статистичних параметрів їх ефективним розрахункових
- 23. Ефективний коефіцієнт водопровідності, визначений за кутовим коефіцієнтам
- 24. Моделювання неоднорідності фільтраційних процесівБули побудовані моделі неоднорідного
- 25. Схема моделі хаотичної фільтраційної неоднорідності
- 26. Моделювання неоднорідності фільтраційних процесівУ першій, другій і
- 27. Моделювання неоднорідності фільтраційних процесівЗа результатами моделювання будувалися
- 28. Висновок по моделіЯк випливає з вищевикладеного, значення
- 29. ХАРАКТЕР ДЕФОРМАЦІЇ ДОСЛІДНИХ ЗАКОНОМІРНОСТЕЙ ЗМІНИ РІВНЯ В ХАОТИЧНО НЕОДНОРІДНИХ ПЛАСТАХ
- 30. Модель – завдання 4Аналіз закономірностей зміни рівня
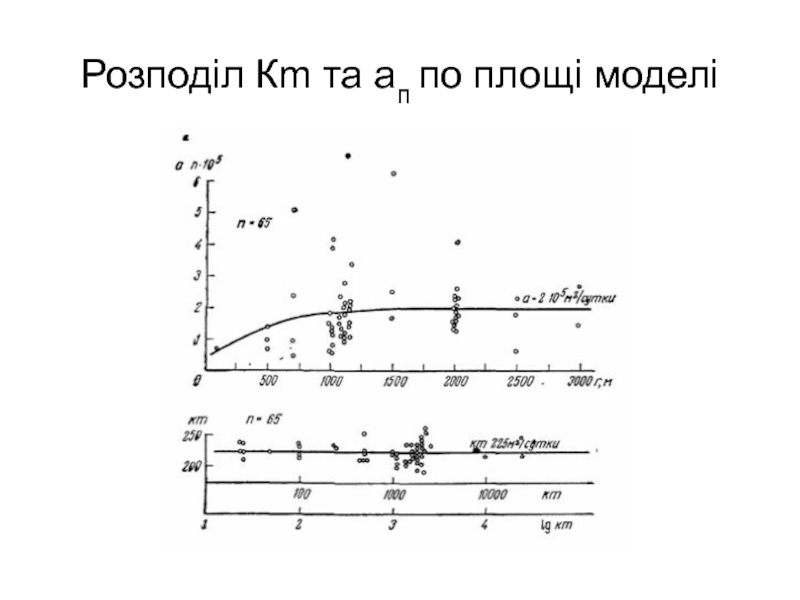
- 31. Розподіл Кm та ап по площі моделі
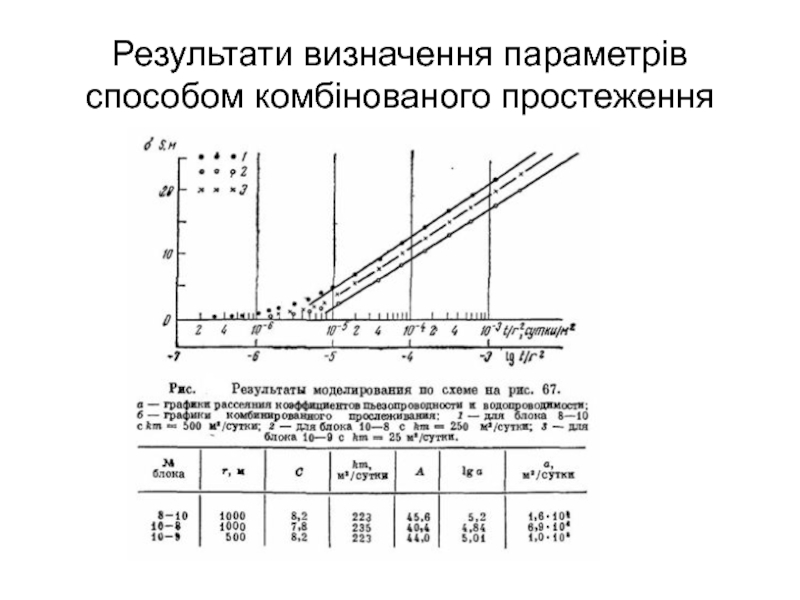
- 32. Результати визначення параметрів способом комбінованого простеження
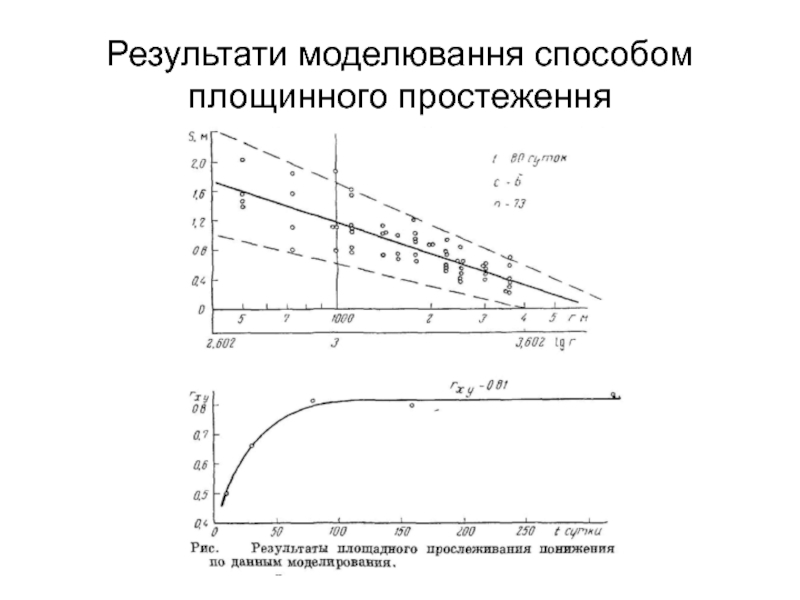
- 33. Результати моделювання способом площинного простеження
- 34. Результати моделювання способом площинного простеженняНа рис.↑ показані
- 35. Використання коефіцієнта кореляції при визначенні параметрівФункціональна залежність
- 36. Результати площинного простеження Результати розрахунків поміщені
- 37. ПРИКЛАДИ ВИЗНАЧЕННЯ ПАРАМЕТРІВ У ХАОТИЧНО НЕОДНОРІДНИХ ПЛАСТАХ
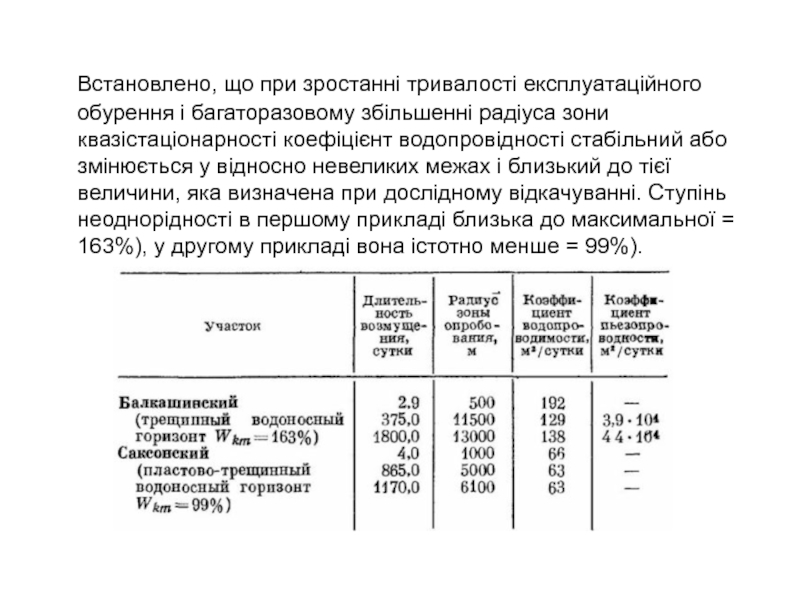
- 38. Встановлено, що при зростанні тривалості
- 39. . З наявного в нашому розпорядженні фактичного
- 40. Слайд 40
- 41. Як видно, відносний розмах величин Km, отриманих
- 42. Визначення параметрів способом площинного простеження.
- 43. Висновки1.Фільтраційна неоднорідність з точки зору тривалості відкачування
- 44. Висновки3. В умовах неоднорідності нижчого порядку зберігаються
- 45. Висновки5. Ефективний коефіцієнт п’єзопровідності можна визначати на
- 46. Скачать презентанцию
Вплив та види неоднорідностіБільшість методів визначення параметрів призначена для умов однорідних водоносних пластів. В реальних умовах неоднорідність є неодмінною властивістю всіх геологічних об'єктів. При обробці дослідних даних методом Джейкоба, неоднорідність водоносних
Слайды и текст этой презентации
Слайд 1
ВИЗНАЧЕННЯ І КВАЛІФІКАЦІЯ ОСНОВНИХ РОЗРАХУНКОВИХ ПАРАМЕТРІВ В УМОВАХ
ХАОТИЧНОЇ
НЕОДНОРІДНОСТІ ФІЛЬТРАЦІЙНИХ ВЛАСТИВОСТЕЙ ПЛАСТА
Слайд 2Вплив та види неоднорідності
Більшість методів визначення параметрів призначена для умов
однорідних водоносних пластів.
В реальних умовах неоднорідність є неодмінною властивістю
всіх геологічних об'єктів. При обробці дослідних даних методом Джейкоба, неоднорідність водоносних пластів виступає як фактор аномальність.
Вид і ступінь аномальності дослідних закономірностей зміни рівня будуть залежати від характеру неоднорідності.
Геологічним об'єктам властиві два види неоднорідності – закономірна та хаотична.
Слайд 3Закономірна неоднорідність
Закономірна неоднорідність пов'язана з наявністю літолого-фаціальних кордонів,
плікативних і розривних тектонічних порушень, тобто це по суті його
структурна неоднорідність.Вона схематизується геометричними формами з межами значної протяжності і різної природи.
Слайд 4Хаотична неоднорідність
Хаотична неоднорідність пов'язана з сингенетичними відмінностями і цілим рядом
епігенетичних проявів в межах одного шару.
Елементи хаотичної неоднорідності, як правило,
значно менше області дослідного, а тим більше експлуатаційного збурення. Якщо елементи хаотичної неоднорідності порівнянні з областю дослідного обурення, їх роль у формуванні фільтраційного потоку аналогічна дії структурної неоднорідності.
Слайд 5Відносність поняття
фільтраційної неоднорідності
Залежно від обсягу
зони випробування один і той масив або водоносний горизонт представляється
неоднорідним чи квазіодноріднимПрактично розрізняється *;
– неоднорідність вищого порядку;
– ефективна неоднорідність;
– неоднорідність нижчого порядку.
*(Рац М.В. “Неоднородность горніх пород и их физические свойства” М.Наука,1967)
Слайд 6Характер неоднорідності
(за М.В. Рацем)
Неоднорідність вищого порядку обумовлена нерівномірним чергуванням
елементів, лінійні розміри яких в 104 і більше разів менше
зони випробування.Ефективна неоднорідність обумовлена нерівномірним чергуванням елементів розмірами в 10 - 100 разів менше розмірів зони випробування.
Неоднорідність нижчого порядку має місце при розмірах елементів більше розмірів зони випробування.
Предметом подальшого розгляду є переважно ефективна неоднорідність в межах елементів неоднорідності нижчого порядку, розміри яких перевищують розміри зони випробування
Слайд 8Основні теоретичні положення
Під хаотичною фільтраційною неоднорідністю водоносного пласта,
мають на увазі неоднорідність водопровідності по площі,
При
цьому зміни водовіддачі практично незначні і ними мжна знехтувати. Дослідження хаотичної неоднорідності виконують на основі статистичної моделі фільтраційного поля, зокрема, на моделі випадкових величин. При цьому припускають, що водопровідність в хаотично неоднорідному пласті є випадкова функція координат.
Слайд 9Основні теоретичні положення
Обсяг інформації, укладений в результатах випробування залежить від
тривалості обурення, З цієї точки зору результати випробування хаотично неоднорідного
пласта системою короткочасних збурень за деякою рідкісної мережі можна розглядати як вибірку випадкових і незалежних показників фільтраційних властивостей з генеральної сукупності.Кожне окреме значення цієї вибірки, що отримується за даними збурення в одній свердловині, розглядається як умовно локальна характеристика з масштабами осереднення значно меншими, ніж розміри досліджуваного фільтраційного поля.
Слайд 10Основні теоретичні положення
Статистичні оцінки, одержувані на основі таких вибірок, характеризують
узагальнені фільтраційні властивості апробованого пласта і ступінь неоднорідності.
Необхідні для
розрахункового прогнозу показники визначаються за законами сучасної теорії оцінок, а також вибір оцінює функції для невідомого параметра генеральної сукупності з безлічі можливих оцінок, базується на критерії Р.А. Фішера. Слайд 11Основні теоретичні положення
На основі цього методу доведено, що достовірними, ефективними,
незміщеними і достатніми оцінками нормального розподілу є середньоарифметичне і середньоквадратичне
відхилення.Такими ж оцінками для логарифмічно нормального розподілу будуть максимальна правдоподібне середнє і середнє квадратичне логарифмів.
Знаходження статистичних оцінок, які відповідають критеріям Фішера, не представляє суттєвої складності при нормальному і логарифмічно нормальний розподіл.
Для більш складних випадків це завдання ускладнюється відсутністю типових рішень оцінюваної функції.
Слайд 12Основні теоретичні положення
Також важливим є питання про відповідність достовірних, ефективних,
незміщене і достатніх оцінок, які визначаються на основі статистичної обробки
результатів випробування пласта одиночними короткочасними збуреннями, і гідродинамічно ефективних параметрів, що визначають реакцію водоносного пласта на збурення і одержуваних більш тривалими збуреннями, область яких значно перевищує розміри елементів неоднорідності.Слайд 13Основні теоретичні положення
При різних законах розподілу статистичні оцінки параметрів виявляються
різними.
Суттєве значення має питання про закон розподілу дослідних сукупностей.
В даний час немає задовільного теоретичного обґрунтування будь-якого закону розподілу ймовірностей водопровідності.
Автори ряду робіт, на підставі позитивного результату оцінок гіпотез про розподіл вибірок, прийшли до переконання, що розподіл водопровідності близько до логарифмічно нормальному і в меншій кількості випадків до нормального законам.
Слайд 14Основні теоретичні положення
Необхідно відзначити, що висновок щодо статистичної перевірки гіпотез
про який суперечить тому чи іншому закону залежить від розміру
вибірки.Зокрема, ймовірність того, що гіпотеза про не суперечити нормальному або логарифмічно нормальному закону не відкидається, підвищується зі зменшенням вибірки.
На практиці звичайно починають працювати з малими вибірками, тому результат перевірки гіпотез про розподіл є досить умовним, часто гіпотези про нормальний і логарифмічно нормального законі відкидаються і при малих вибірках.
Слайд 15КЛАСИФІКАЦІЯ ВОДОВМІСНИХ
ПОРІД ЗА СТУПЕНЕМ
ХАОТИЧНОЇ НЕОДНОРІДНОСТІ
І ЗВЯЗОК ЕФЕКТИВНИХ ГІДРОГЕОЛОГІЧНИХ
ПАРАМЕТРІВ
ІЗ СТАТИСТИЧНИМИ ОЦІНКАМИ
Слайд 16Основні класифікаційні показники
Отримані статистичні оцінки можна використовувати для відносної характеристики
ступеня неоднорідності водопровідності, зокрема, як класифікаційні показнику.
Основою класифікації фільтраційної неоднорідність
виступає коефіцієнт водопровідності. Як ознаку відносної характеристики неоднорідності, можна використовувати питомий дебіт однотипно обладнаних свердловин.
Слайд 17Стастичні оцінки показників фільтраційної неоднорідності
Показники неоднорідності вибираються з числа
статистичних показників розсіювання вимірюваної ознаки.
До таких показників відноситься:
– розмах вибірки ( R );– середнє квадратичне відхилення (σ чи σlg);
– дисперсія (S чи Slg);
– коефіцієнт варіації (W).
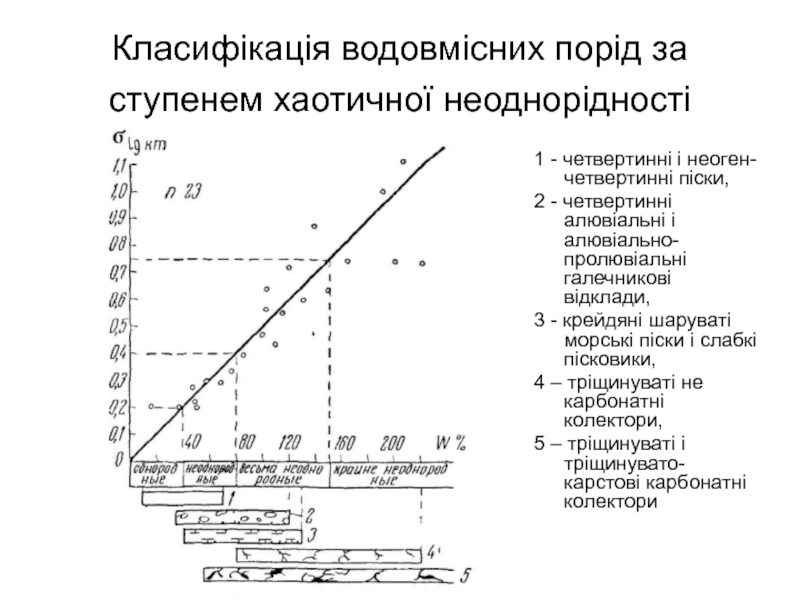
Слайд 18Класифікація водовмісних порід за ступенем хаотичної неоднорідності
1 - четвертинні
і неоген-четвертинні піски,
2 - четвертинні алювіальні і алювіально-пролювіальні галечникові
відклади,3 - крейдяні шаруваті морські піски і слабкі пісковики,
4 – тріщинуваті не карбонатні колектори,
5 – тріщинуваті і тріщинувато-карстові карбонатні колектори
Слайд 19Вивчення мінливості коефіцієнта водопровідності (питомого дебіту) спирається на матеріали розвідки
по 100 дільницям.
Для аналізу використано фактичний матеріал по малим
вибірками, що включають 10 -15 значень. Окремі положення, на прикладі ще 30 вибірок більшого розміру - 15-90 з переважанням 25-30 значень.
На прикладі зазначеної кількості вибірок, що представляють широкий діапазон водовмісних порід, встановлено, що всі випадки знаходяться в інтервалі середнього квадратичного логарифмів σlg = 0,05 - 1,3 і коефіцієнта варіації W - 15-220%,
В основному розподіл не суперечать логарифмічно нормальному закону, іноді не суперечать нормальному закону і в рідкісних випадках суперечать обом законам.
За результатами обробки безлічі вибірок відзначається цілком певний зв'язок середнього квадратичного логарифмів і коефіцієнта варіації з типом колекторів (див. табл. ↓).
Слайд 21 Зв’язок нормального закону з числом каналів фільтрації.
дозволяє виділити за цією ознакою типи розподілу проникності для грубо-пористих
і дрібнопористих порід. На наявних прикладах можна було переконатися, що відповідність нормальному розподілу, можна зустріти і серед пористих однорідних колекторів (W = 50%), і серед досить неоднорідних тріщинних колекторів (W = 200%).Виділені групи колекторів, відмінності яких заздалегідь відомі, відрізняються величинами середніх σlg і W і протяжністю їх інтервалів. Все різноманіття в різного ступеня неоднорідних водоносних горизонтів доцільно поділити за величинами середнього квадратичного логарифма і коефіцієнта варіації на чотири групи незалежно від типу розподілу.
Слайд 22
Відповідності статистичних параметрів їх ефективним розрахункових значень.
Під ефективними параметрами
при цьому розуміються значення водопровідності й п’єзопровідності такого однорідного водоносного
горизонту, в якому розрахункові значення знижень рівня в зоні квазістаціонарного режиму на певні моменти часу близькі до значень знижень в розглянутому неоднорідному пласті.Для аналізу цього питання використовуємо експериментальні дані отримані при застосуванні методів аналогового моделювання. Подібне завдання стосовно нормальyому розподілу ставилася І.С.. Пашковським [94], на електропровідною папері було створено кусково-неоднорідне поле, провідність якого змінювалася в межах 0-200 м2/доба. Математичне очікування нормально розподіленої сукупності окремих значень дорівнювало 100 м2/доба, стандартне відхилення 50м2/доба і коефіцієнт варіації 50%.
Слайд 23Ефективний коефіцієнт водопровідності, визначений за кутовим коефіцієнтам графіків часового простеження
зниження, виявився рівним математичному очікуванню, яке при заданому нормальному законі
рівно середньому арифметичному.Таким чином, наведений приклад показує, що величини ефективного коефіцієнта водопровідності і середнє арифметичного при нормальному розподілі збігаються.
Відповідність статистичних оцінок і гідродинамічних ефективних значень параметрів при інших законах розподілу перевірялося за допомогою моделювання на сіткових моделях.
Були побудовані моделі неоднорідного пласта з незакономірним розташуванням елементів неоднорідності, розподіл яких або не суперечило логарифмічно нормальному закону, або не відповідало як нормальному так і логарифмічно нормальному закону.
Гіпотеза про закон розподілу перевірялася за критерієм Пірсона
Всього було розглянуто чотири моделі (три при логарифмічно нормальному і одна при невизначеному законі розподілу), що відрізняються величиною середньоквадратичного відхилення логарифма водопровідності (а). Положення елементів неоднорідності визначалося жеребкув
Слайд 24Моделювання неоднорідності фільтраційних процесів
Були побудовані моделі неоднорідного пласта з незакономірним
розташуванням елементів неоднорідності, розподіл яких або не суперечив логарифмічно нормальному
закону, або не відповідав як нормальному так і логарифмічно нормальному закону.Гіпотеза про закон розподілу перевірялася за критерієм Пірсона
Всього було розглянуто чотири моделі (три при логарифмічно нормальному і одна при невизначеному законі розподілу), що відрізняються величиною середньоквадратичного відхилення логарифма водопровідності σlg(km).
Слайд 26Моделювання неоднорідності фільтраційних процесів
У першій, другій і третій задачах розглядався
ряд варіантів з різним розташуванням дослідних свердловини Результат статистичної обробки
показаний в таблиці:Слайд 27Моделювання неоднорідності фільтраційних процесів
За результатами моделювання будувалися графіки S−lg(t0, S−lg®,
S−lg(t/r2) та аналізувався вид цих графіків і визначалися основні гідрогеологічні
параметри (коефіцієнти водопровідності і п’єзпровідності). результати розрахунку показані в таблиці.Слайд 28Висновок по моделі
Як випливає з вищевикладеного, значення ефективного коефіцієнта водопровідності
при нормальному розподілі близькі до середнього арифметичного, при логарифмічно нормальному
– середньому геометричному (розбіжності не перевищують 20%), при нерегулярному розподілі не контролюються статистичними оцінками.Розбіжність між середньою арифметичною величиною водопровідності і ефективним її значенням при логарифмічно нормальному і нерегулярному розподілі дуже істотні, причому ця різниця збільшується зі зростанням ступеня неоднорідності водоносного горизонту. Так, якщо при σ = 0,5 середнє арифметичне перевищує ефективне в 2,2 рази, то при σ = 0,7 та σ = 0,99 відповідно в 3,6 і 18 разів.
Чисельний аналіз оцінок середнього при логарифмічно нормальному розподіл показує, що при (σlg < 0,3) відмінність між середнім арифметичним і середнім геометричним несуттєва.
Слайд 30Модель – завдання 4
Аналіз закономірностей зміни рівня в хаотично неоднорідному
пласті проведено за результатами моделювання досить неоднорідного водоносного пласта (завдання
4).Середньоквадратичне логарифмів σlg = 0,99 і коефіцієнт варіації W = 190% цього пласта характеризують найбільшу хаотичну неоднорідність.
Розміщення елементів неоднорідності в основній частині фільтраційного частка і задані умови видно на схемі моделі. Тут показані ізолінії зниження на момент = 30 діб. В наступні моменти часу (t - 80, 160, 320 діб) рельєф депресійної воронки, зафіксований на момент t = 30 і 10 діб, практично не змінювався.
Результати моделювання оброблені способом часового, площинного і комбінованого простеження. Результати представлені на рис↓.
Слайд 34Результати моделювання способом площинного простеження
На рис.↑ показані результати площинного простеження
зниження. Графік площинного простеження, побудований на момент t = 80
діб, представлений хмарою точок, витягнутим по осі відстаней; ступінь розсіювання зменшується з віддаленням від дослідного блоку. Характер розсіювання не змінюється для пізніх моментів простеження (t = 160 та 320 діб), але змінюється для ранніх моментів (t = 10, 30 діб).Таким чином, в пластах з хаотичною неоднорідністю, ступінь якої характеризується в даному випадку коефіцієнтом варіації W = 190%, в порівнянні з однорідними шарами спостерігається порушення лінійної напівлогарифмічної площинної залежності
Слайд 35Використання коефіцієнта кореляції при визначенні параметрів
Функціональна залежність (рис.↑) переходить в
кореляційну. Емпіричний коефіцієнт кореляції (rx,y). визначається за формулою:
Коефіцієнт кореляції визначено
для графіків площинного простеження на моменти: t - 10; 30; 80; 160; 320 діб. Результати визначень представлені у вигляді графіка rx,y = f(t) показаний на рис. 69. У інтервалі 10-50 діб, тобто в межах практичної тривалості досліду, коефіцієнт кореляція знаходиться в межах rx,y = 0,5-0,7, характеризуючи слабкий зв'язок зниження з логарифмом відстані. Пізніше відзначається постійний і помітна зв’язок цих величин, так як rx,y стає постійним і рівним 0,8. Переконавшись в помітній кореляційної площинної базарною закономірності, визначимо параметри досліджуваного водоносного пласта через коефіцієнт лінійної регресії b – кутовий коефіцієнт графіка простеження, що дозволяє застосувати метод Джейкоба для розрахунку параметрів
Слайд 36Результати площинного простеження
Результати розрахунків поміщені склали: km =
260 м2/доба, а = 2,9-105 м2/доба.
Отримані величини близькі
до результатів отриманих за комбінованим простеженням (табл. ↑). Отримані параметри повністю визначають часову і наближено площинну закономірність зміни рівня в апробованому пласті. Як уже говорилось, такі параметри можна кваліфікувати як ефективні. Порівнння результатів показано в таблиці
Слайд 38 Встановлено, що при зростанні тривалості експлуатаційного обурення і
багаторазовому збільшенні радіуса зони квазістаціонарності коефіцієнт водопровідності стабільний або змінюється
у відносно невеликих межах і близький до тієї величини, яка визначена при дослідному відкачуванні. Ступінь неоднорідності в першому прикладі близька до максимальної = 163%), у другому прикладі вона істотно менше = 99%).Слайд 39. З наявного в нашому розпорядженні фактичного матеріалу відібрані дослідні
ділянки з різною і значним ступенем неоднорідності, вимірюваної среднє квадратичне
логарифмів питомого дебіту і коефіцієнта варіації: σlg − 0,29-1,29; W − 61-145%.Відкачування в межах аналізованих ділянок виконувалось декількома дослідними кущами, області впливу яких радіусом не менше 1 км перекривалися частково або повністю.
Виняток становить лише Урулюнгуйська ділянка, де області впливу відкачування роз'єднані.
Коефіцієнт водопровідності визначений способом часового простеження по п'яти - восьми спостережних свердловинах.
При аналізі мінливості Km в межах куща використовується його середнє арифметичне і розмах R - різниця між крайніми значеннями водопровідності.
Підсумковою величиною є відносний розмах. Результати аналізу зведені в табл.↓.
Слайд 41Як видно, відносний розмах величин Km, отриманих за даними часового
простеження зниження, знаходиться в межах 12-44%, причому характерна відсутність зв’язку
між величиною розмаху і ступенем неоднорідності ділянки. Остання обставина свідчить про те, що наявні відмінності в величинах водопровідності не пов’язані з природою неоднорідності. Дійсно, аналіз кожного об’єкта окремо показує, що на ділянках Лівобережний, Аймурзінскій і Урулюнгуйській розбіжності були наслідком недосконалості спостережних свердловин в анізотропному розрізі. Крім того, розбіжності обумовлені похибками обробки.На прикладі ділянок Мійкайнар, Аймурза, Майлисай видно, що визначаються параметри практично не залежать і від місця розташування дослідної свердловини, якщо зміна розташування відбувається в загальній області впливу відкачування. Розбіжності при зміні дослідних свердловин не перевищують 20%.
Слайд 42Визначення параметрів способом площинного простеження.
Площинні закономірності
зміни рівня в хаотично неоднорідних пластах є кореляційними. При цьому
встановлено, що мірою зв'язку і критерієм для класифікації є величиною коефіцієнта варіації (W). Для основних груп водоносних горизонтів, виділених за ступенем неоднорідності, характерні наступні значення коефіцієнта кореляції:W,% rxy
однорідні <40 0,99-0,95
неоднорідні 40-80 0,95-0,90
дуже неоднорідні 80-150 0,90-0,80
вкрай неоднорідні >150 << 0,8
Як показує аналіз дослідних графіків площинного простеження, кореляційний залежність зниження від логарифма відстані досить значна. Для практичниї розрахунків геобхідна достатня кількість спостережних свердловин. Для однорідних водоносних пластів, що характеризуються ступенем неоднорідності W=40% і силою кореляційної зв'язку площинних графіків 0,99-0,95, кількість спостережних свердловин може бути мінімальною.
Слайд 43Висновки
1.Фільтраційна неоднорідність з точки зору тривалості відкачування є поняттям відносним.
Характер неоднорідності визначається відносними (по відношенню до розмірів області впливу
відкачування) розмірами елементів неоднорідності. За характером деформації дослідних закономірностей зміни рівня доцільно розрізняти ефективну неоднорідність і неоднорідність нижчого порядку (по М. Б. Рацу).2. В умовах ефективної неоднорідності часові закономірності зміни рівня зберігаються функціональними, а площинні - переходять в кореляційні. За дослідними даними встановлена залежність сили кореляційної зв'язку {гху) від ступеня неоднорідності.
Слайд 44Висновки
3. В умовах неоднорідності нижчого порядку зберігаються функціональними і часові,
і площинні закономірності зміни рівня, але часові закономірності з часом
змінюють вигляд функціональної залежності; деформації площинних закономірностей менш помітні і мають місце на ділянках в периферійних частинах депресії (г> 0,5 l). Для площинних закономірностей характерні паралельні зміщення графіків, побудованих на пізні моменти часу.4. В умовах ефективної неоднорідності параметри визначаються способом часового (комбінованого) простеження. Параметри є гідро динамічно ефективними. Необхідність усереднення одержуваних величин існує тільки щодо коефіцієнта п’єзопровідності (рівнепровідності) в досить неоднорідних і вкрай неоднорідних середовищах (W > 80%).
Слайд 45Висновки
5. Ефективний коефіцієнт п’єзопровідності можна визначати на основі середнього арифметичного.
Визначення ефективних параметрів способом площинного простеження можливо по декількох спостережних
свердловинах, число яких залежить від ступеня неоднорідності. Можливість визначення ефективних параметрів за формулою Дюпюї за двома спостережними свердловинами обмежується однорідними водоносними горизонтами (W <30% -40%).6. У зв'язку з тим, що в реальних умовах ефективні значення параметрів навіть при тривалих відкачках можуть бути визначені далеко не у всіх випадках (особливо для безнапірних горизонтів), необхідно за даними дослідних робіт визначати характер і ступінь неоднорідності і відповідно до отриманих результатів вибирати метод оцінки експлуатаційних запасів підземних вод і розрахункові параметри для прогнозу.