Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Восточная преднаука
Содержание
- 1. Восточная преднаука
- 2. Вопросы лекцииПроблема генезиса наукиСистема знаний Древнего Востока
- 3. 1. Проблема генезиса наукиМиф как основание науки.Философия как основание науки.
- 4. 2. Система знаний Древнего ВостокаА) Практические знания
- 5. а) Практические знанияВ эпоху
- 6. Слайд 6
- 7. Практические знания4. Человек владел знаниями материалов. Получал
- 8. Практические знания6. Некоторые механизмы, применяемые ремесленниками, чуть
- 9. В) Абстрактные знанияМатематикаАстрономия
- 10. Возникновение математических знанийИероглифические непозиционные системы счета.
- 11. Возникновение математических знаний2. Алфавитные системы счисления. В
- 12. Возникновение математических знаний3. Позиционные недесятичные, а затем
- 13. Создание календаря в ЕгиптеГосударственное регулирование производства диктовали
- 14. Зарождение астрономических знаний в МесапотамииПродолжительность лунного года
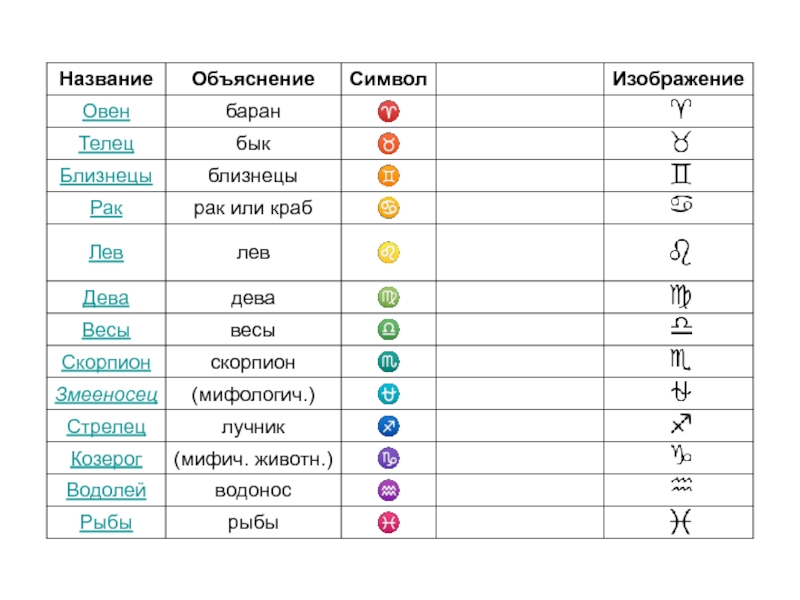
- 15. Зодиакальный пояс. Пересечения плоскости эклиптики и плоскости
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
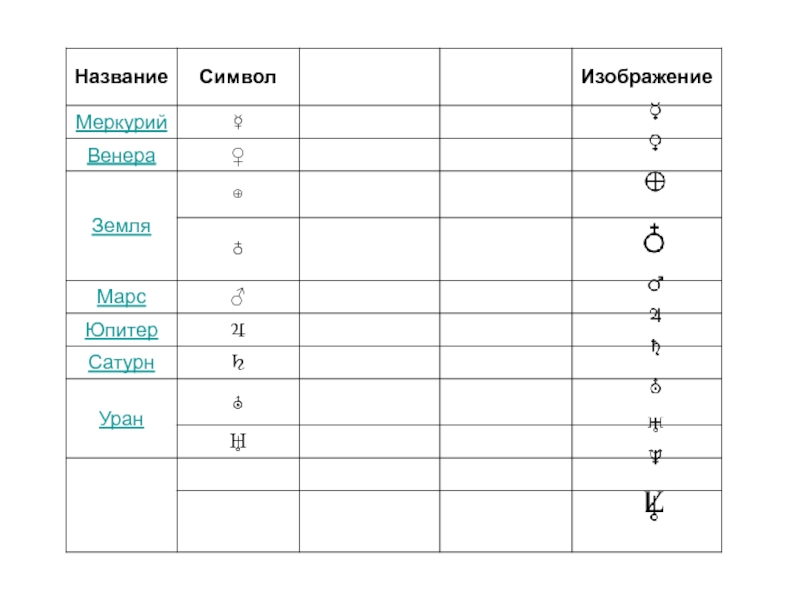
- 19. Астрономия Месапотомамиизвёзды бога Эа (бог Воды), идущая
- 20. Астрономия МесапотомамииАстрологический сборник того времени "Энума ,
- 21. МатематикаНаиболее высокого уровня развития достигла математика Древнего
- 22. МатематикаСуществовали таблицы умножения, таблицы квадратов и кубов
- 23. Математика (Египет)При решении задач используются действия с
- 24. Математика (Египет)Вычислительная техника была аддитивной. Все процедуры,
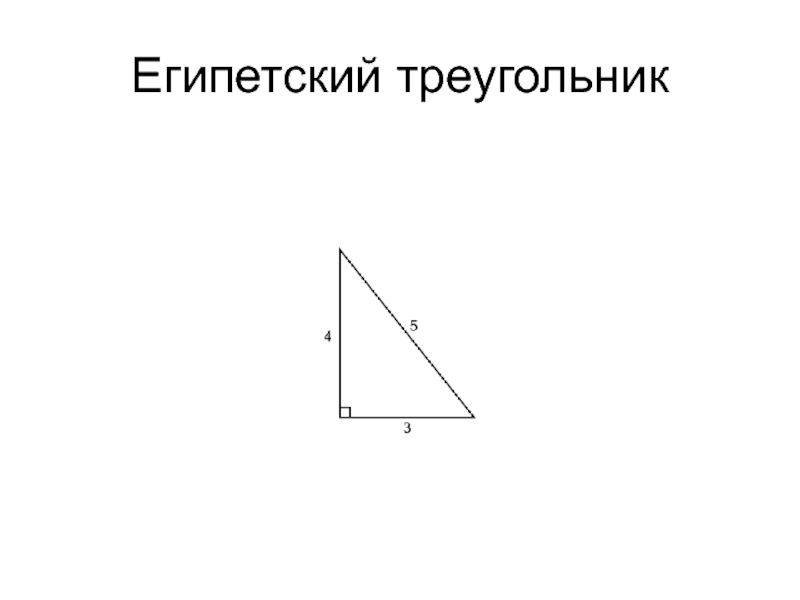
- 25. Египетский треугольник
- 26. Часы (Египет)Клепсидра — водяные часы
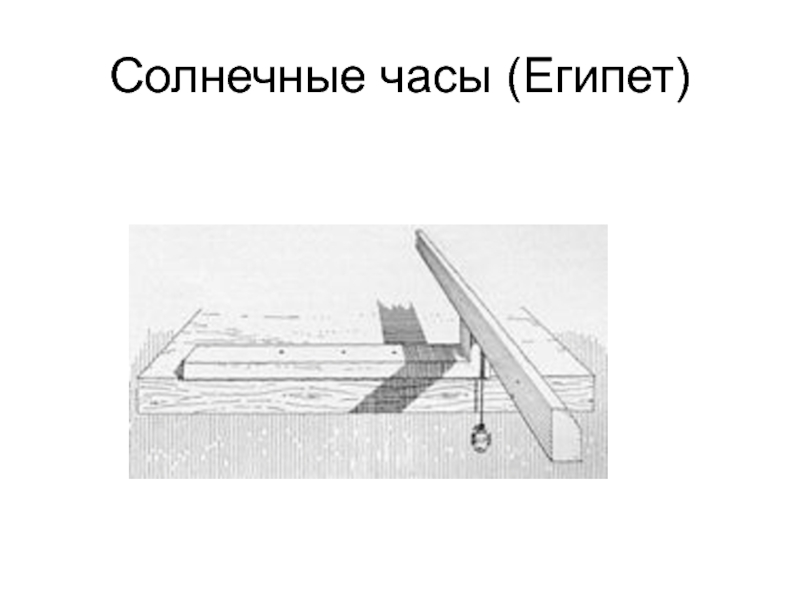
- 27. Солнечные часы (Египет)
- 28. Солнечные часыПервым о солнечных часах упомянул китаец
- 29. Солнечные часыДо нашего времени сохранился египетский обелиск,
- 30. В 1792 г. этот обелиск вновь
- 31. Китай Модель небесной сферы «Тян хэн». Прибор
- 32. 3. Особенности Восточной преднаукиНаука имела прикладной характер,
- 33. Особенности Восточной преднаукиРецептурно-алгоритмический характер знаний. Записывались конкретные задачи и их решения.
- 34. Особенности Восточной преднауки3. Научные знания были отделены
- 35. Особенности Восточной преднауки4. Центрами аккумуляции научных знаний
- 36. Особенности Восточной преднауки5. Элементы научного знания тесно
- 37. Особенности Восточной преднауки6. Специфическое положение науки в
- 38. Скачать презентанцию
Вопросы лекцииПроблема генезиса наукиСистема знаний Древнего Востока (Древнего Египта, Древнего Вавилона, Древнего Китая, Древней Индии)Преднаука Древнего Востока (Математика, Астрономия) Особенности Восточной преднауки
Слайды и текст этой презентации
Слайд 2Вопросы лекции
Проблема генезиса науки
Система знаний Древнего Востока (Древнего Египта, Древнего
Вавилона, Древнего Китая, Древней Индии)
Восточной преднаукиСлайд 42. Система знаний Древнего Востока
А) Практические знания – знания, которые
не записываются, передаются в процессе деятельности
В)Абстрактные знания, которые записываются
Слайд 5
а) Практические знания
В эпоху бронзы человек изобрел государственность
В
государствах периода бронзы человек умел строить сложные ирригационные системы, особенно
в Древнем Египте и Вавилоне; управлять разливом рек, орошать поля при помощи каналов. Изобрел водоподъемное устройство – «журавль».Человек умел строить гигантские сооружения – пирамиды, используя при этом разнообразную строительную технику, простые машины: клин, наклонные плоскости, рычаги, качалки, блоки, вороты.
Слайд 7Практические знания
4. Человек владел знаниями материалов. Получал очень высокого качества
кирпич, в том числе (обожженный и глазурованный), черепицу, известь, цемент.
В Египте варили стекло, причем разноцветное. Знали различные пигменты-красители. Керамика получила дальнейшее развитие.5. Человек освоил металлы. Он знал семь металлов: золото, серебро, медь, олово, свинец, ртуть, железо, а также сплавы между ними: бронзы (медь с мышьяком, оловом или свинцом) и латуни (медь с цинком). Цинк и мышьяк использовались в виде соединений. Существовала и соответствующая техника для плавки металлов: печи, кузнечные мехи и древесный уголь как горючее, что позволяло достигнуть температуры 1500 0С для плавления железа.
Слайд 8Практические знания
6. Некоторые механизмы, применяемые ремесленниками, чуть ли не до
сей поры, изобретены в глубокой древности. Например, токарный станок (ручной,
деревообрабатывающий).7. В области торговли использовались весы и деньги.
8. Процветало кораблестроение и мореплавание.
9. Развивалось военное искусство, совершенствовалось оружие: лук, стрелы, дротики, копья, топоры, булавы.
10.В сельском хозяйстве использовали мельницы, в домашнем хозяйстве-прялки. Продолжало развиваться ткачество.
11. Процветали ремесла.
12. Развивалась медицина
Слайд 10 Возникновение математических знаний
Иероглифические непозиционные системы счета. В них существуют
узловые числа (чаще всего – 1, 10, 100, 1000). Каждое
такое число имеет индивидуальный символ – иероглиф. Остальные числа (алгоритмические) образуются приписыванием с той или другой стороны узлового числа других узловых чисел и повторением их.К таким системам относятся египетская, финикийская, сирийская, ацтекская, римская и другие системы счета. В римской системе узловыми числами являлись: I, V, X, L, C, D, M.
Слайд 11Возникновение математических знаний
2. Алфавитные системы счисления. В этих системах буквы
алфавита, взятые по 9, используются для обозначения единиц, десятков, сотен.
Каждой букве дается отличительный знак, что она используется как число, например, палочка сверху.Примером алфавитной системы счета является греческая ионическая система Древнейшая, сохранившаяся ее запись относится к V в. до н.э. К алфавитной системе относятся, древнеславянская (кириллица и глаголица), еврейская, арабская, грузинская, армянская системы счета.
Слайд 12Возникновение математических знаний
3. Позиционные недесятичные, а затем и десятичные системы
счета. К ним относятся: вавилонская (60), индийская системы счета (10).
Запись в позиционной десятичной системе с нулем впервые появились около V в. до н.э. в Индии.
Слайд 13Создание календаря в Египте
Государственное регулирование производства диктовали необходимость разработки точного
календаря, счета времени, а отсюда - астрономических познаний.
Египтяне разработали
календарь, состоящий из 12-ти месяцев по 30 дней и 5-ти дополнительных дней в году. Месяц был разделен на 3 десятидневки, сутки на 24 часа: 12 дневных часов и 12 ночных (величина часа была не постоянной, а менялась со временем года). Слайд 14Зарождение астрономических знаний в Месапотамии
Продолжительность лунного года - 354 дня,
а солнечного - 365 дней. Чтобы в солнечном году умещалось
целое число лунных месяцев, надо было через определенный период вставлять добавочный 13-й месяц.Слайд 15Зодиакальный пояс.
Пересечения плоскости эклиптики и
плоскости орбиты
Луны с
небесной сферой
изображены красной и голубой линиями.
Слайд 19Астрономия Месапотомамии
звёзды бога Эа (бог Воды), идущая вдоль небесного экватора
(проекция Земного экватора на небесной сфере) полосой + 30°,
звёзды
бога Ану (бог Неба) - по склонению от + 30° до + 60° и звёзды бога Энлиля (бог Земли) - околополярные звёзды со склонениями больше 60°.
Слайд 20Астрономия Месапотомамии
Астрологический сборник того времени "Энума , Ану , Энлиль"
был самым основным и важным руководством для практического применения.
Создание
пояса зодиакаСлайд 21Математика
Наиболее высокого уровня развития достигла математика Древнего Вавилона.
Известно 50
табличек математического содержания и 200 таблиц без текста.
Усилия математиков
были сосредоточены на освоение арифметических действий, как с целыми числами, так и с дробями. Слайд 22Математика
Существовали таблицы умножения, таблицы квадратов и кубов целых чисел.
Есть
исчисление процентов за долги.
Вавилоняне знали теорему Пифагора, значение квадратного
корня из 2.Умели решать системы уравнений и квадратные уравнения.
Слайд 23Математика (Египет)
При решении задач используются действия с дробями, вычисляются площади
треугольника, прямоугольника, трапеции, круга.
Площадь круга вычислялась как (8/9 d)².
Египтяне умели вычислять объемы параллелепипеда, цилиндра, пирамиды. В московском папирусе представлены решения 25 задач.
Слайд 24Математика (Египет)
Вычислительная техника была аддитивной. Все процедуры, по возможности сводили
к сложению. Дробь понималась как часть единицы. При умножении использовалось
постепенное удвоение одного из сомножителей, затем следовал подбор подходящих частных произведений.(12·12) 1 12
2 24
*4 48
*8 96
----------------------
Вместе 144
Слайд 28Солнечные часы
Первым о солнечных часах упомянул китаец Чиу-пи (примерно 1100
г. до н. э.). Самые благоприятные климатические условия для измерения
времени солнечными часами имел Египет. Вот поэтому и считают, что первые солнечные часы – гномон, появились именно здесь. Это был вертикальный обелиск со шкалой, которая была нанесена на землю возле него. Также эти обелиски использовали для почитания культа бога Солнца. Они стояли перед входами в храмы.Слайд 29Солнечные часы
До нашего времени сохранился египетский обелиск, высота которого составляет
34 м. История говорит, что во времена правления Августа он
был перевезен из Египта в Рим и установлен на Марсовом поле.Слайд 30 В 1792 г. этот обелиск вновь установили на площади
Монтечиторио в Риме. Здесь он стоит и в наше время.
Слайд 31Китай
Модель небесной сферы «Тян хэн». Прибор состоял из часов,
небесного глобуса
и армиллярной сферы, с помощью которой определялись координаты Солнца, Луны, пяти
планет и звездСлайд 323. Особенности Восточной преднауки
Наука имела прикладной характер, обслуживала практическую деятельность
людей.
Ее вызвали к жизни практические потребности в измерении, сравнении,
обмене предметов, сформировавшиеся в рамках аграрных цивилизаций. Слайд 33Особенности Восточной преднауки
Рецептурно-алгоритмический характер знаний.
Записывались конкретные задачи и
их решения.
Слайд 34Особенности Восточной преднауки
3. Научные знания были отделены от технических. Последние
развивались в рамках ремесел и искусств. Передавались от мастера ученику
без специальных записей, непосредственно.Технические знания не имели форм обобщения.
Слайд 35Особенности Восточной преднауки
4. Центрами аккумуляции научных знаний выступали храмы. Хранителями
знания стали жрецы. Возник такой феномен, как храмовая наука.
Это
привело к тому, что знания догматизировались и сакрализировались, объявлялись священными. Занятия наукой превращались в таинство, а знания превращались в объект поклонения.
В таких условиях знания не могли подвергаться критике, развитие знаний было затруднено.
Слайд 36Особенности Восточной преднауки
5. Элементы научного знания тесно переплетались с вненаучным
знанием:
математика с нумерологией,
астрономия с астрологией,
медицина с магией.
Слайд 37Особенности Восточной преднауки
6. Специфическое положение науки в государствах Древнего Востока
в значительной степени объяснялось социально-политическими условиями: деспотическим характером политической власти,
отсутствием в обществе демократии и достаточного пространства для свободы личности.В обществе со строгой иерархией новое с трудом находило себе дорогу, здесь новация в принципе не приветствовалась, и процедура доказательства, являющаяся неотъемлемым свойством научного знания, оказывалась излишней.