Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
вписанная и описанная окружности
Содержание
- 1. вписанная и описанная окружности
- 2. Тема урока: Описанная и вписанная окружности треугольника
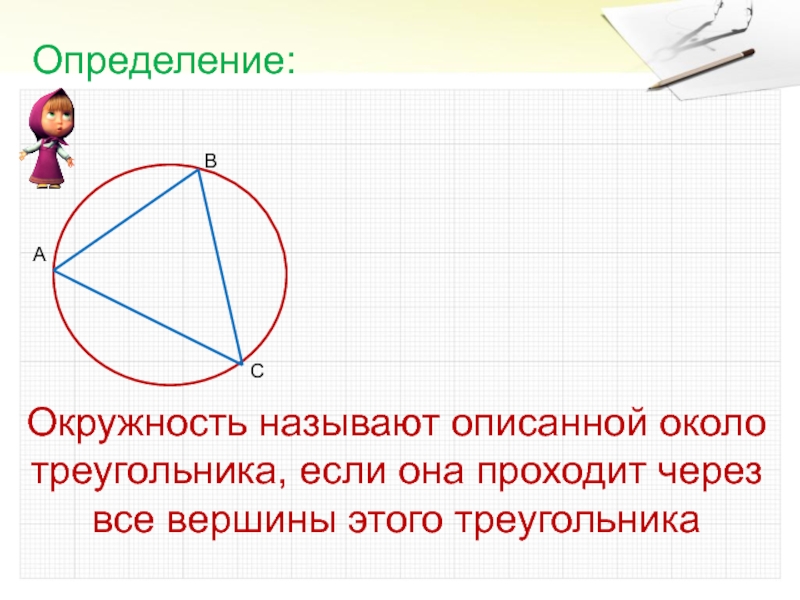
- 3. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника Определение:
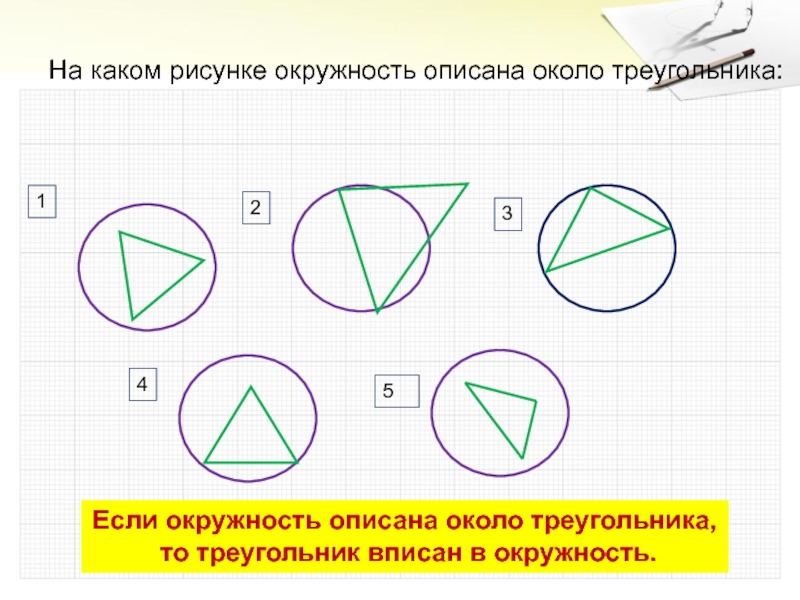
- 4. На каком рисунке окружность описана около треугольника:12345Если окружность описана около треугольника, то треугольник вписан в окружность.
- 5. Около любого треугольника можно описать окружностьЗаметим, около
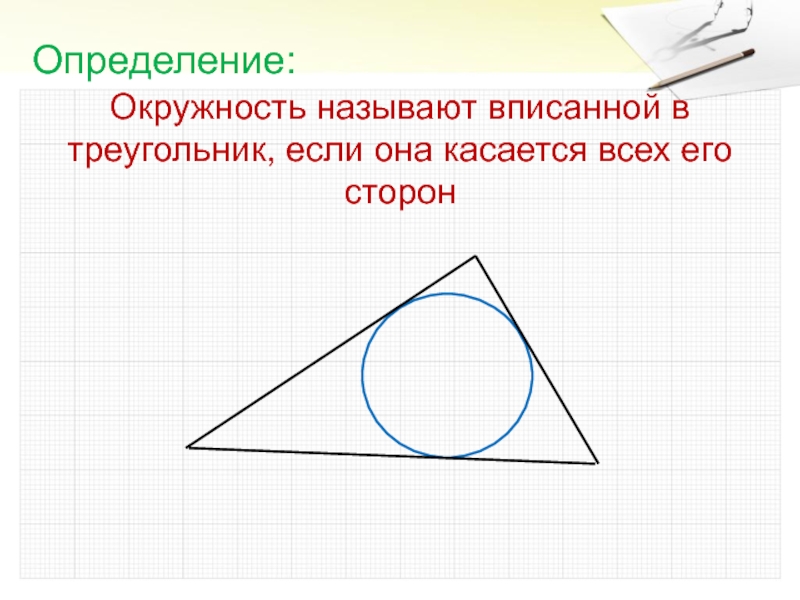
- 6. Окружность называют вписанной в треугольник, если она касается всех его сторонОпределение:
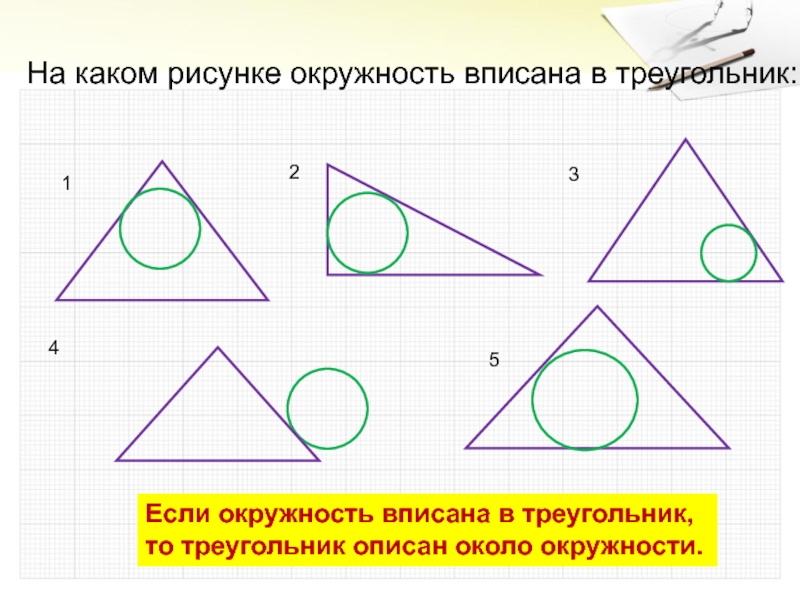
- 7. На каком рисунке окружность вписана в треугольник:134Если окружность вписана в треугольник, то треугольник описан около окружности.25
- 8. Заметим, в треугольник можно вписать окружность,
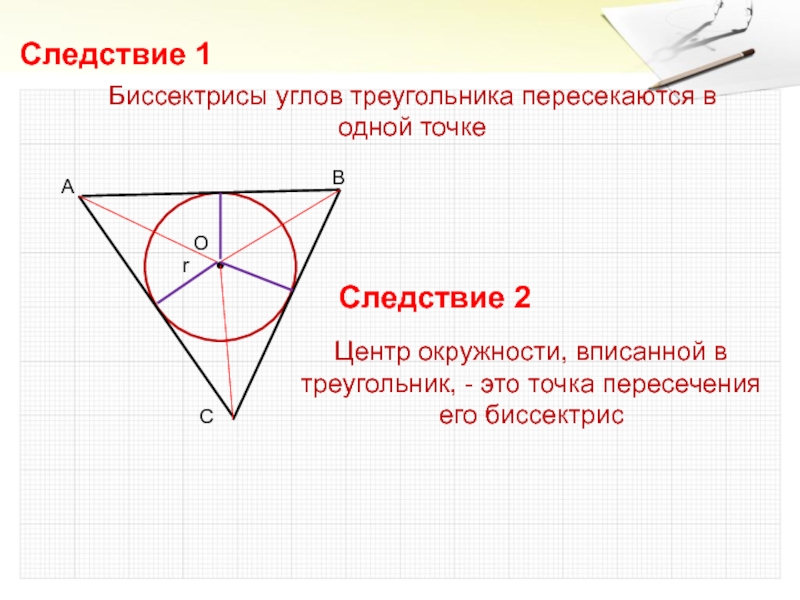
- 9. rБиссектрисы углов треугольника пересекаются в одной точкеСледствие
- 10. Радиус окружности вписанной в прямоугольный треугольник, определяется
- 11. Задачи на построение
- 12. В геометрии выделяют задачи
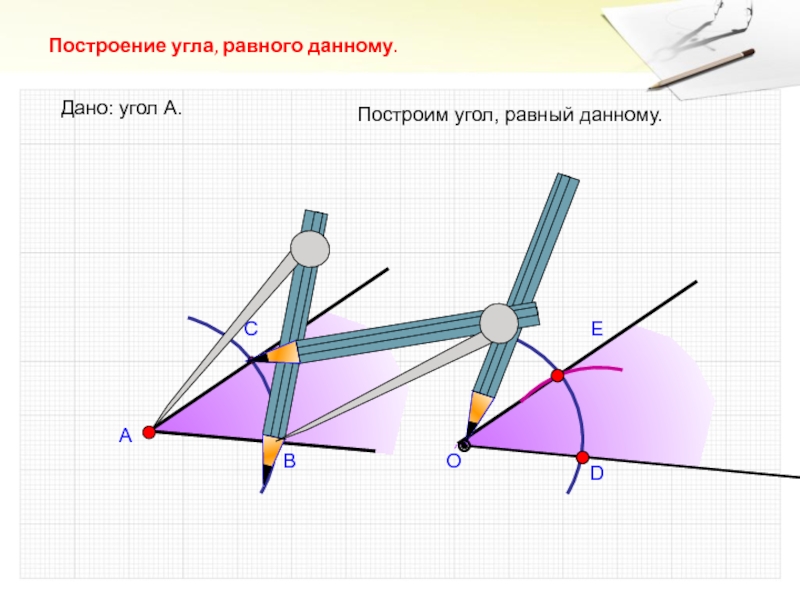
- 13. АВСПостроение угла, равного данному.Дано: угол А.Построим угол, равный данному.ОDE
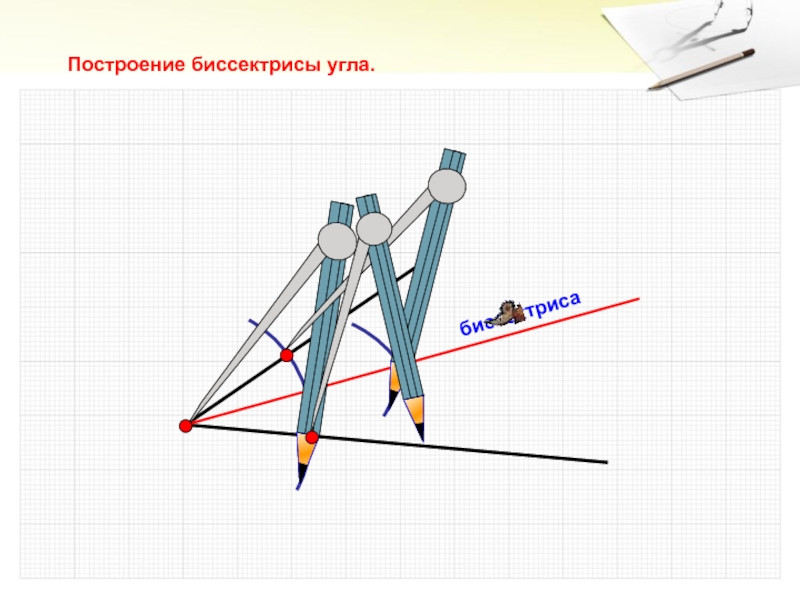
- 14. биссектрисаПостроение биссектрисы угла.
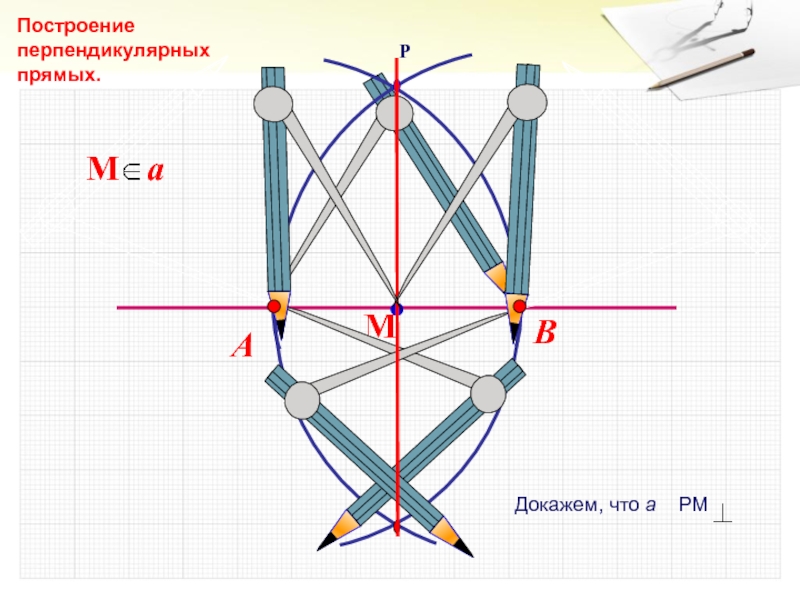
- 15. ВАПостроение перпендикулярных прямых.
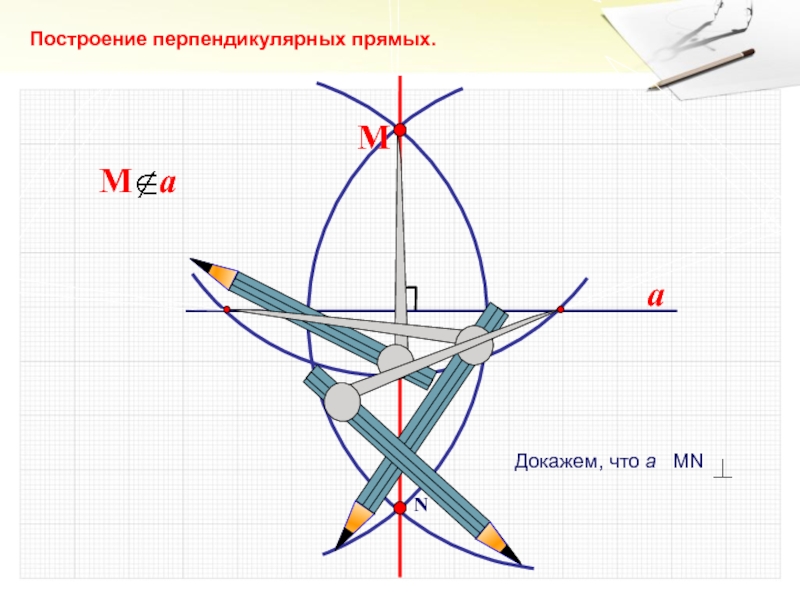
- 16. aNМПостроение перпендикулярных прямых.
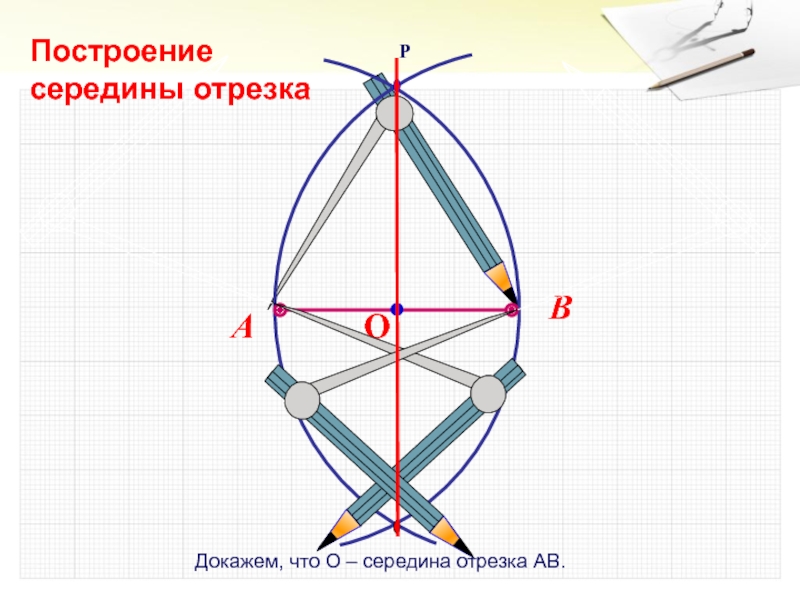
- 17. Докажем, что О – середина отрезка АВ.Построение середины отрезка
- 18. Слайд 18
- 19. Слайд 19
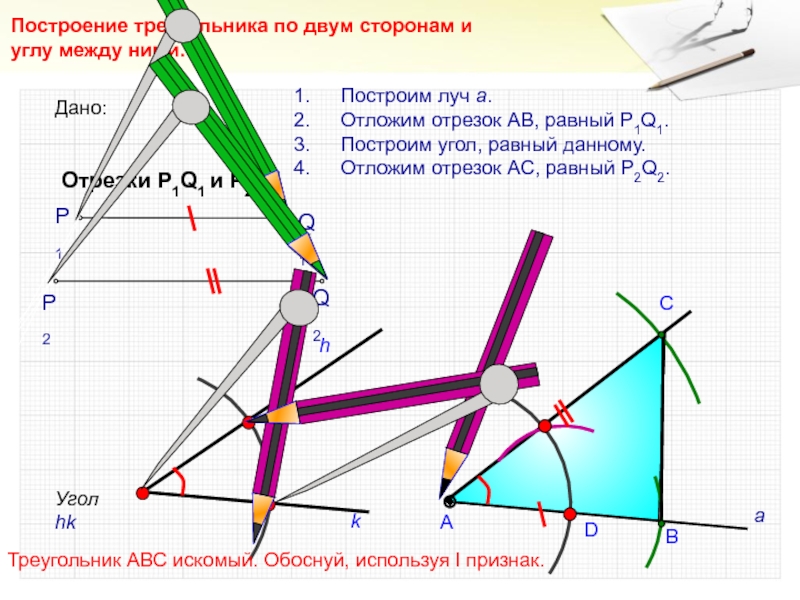
- 20. DСПостроение треугольника по двум сторонам и углу
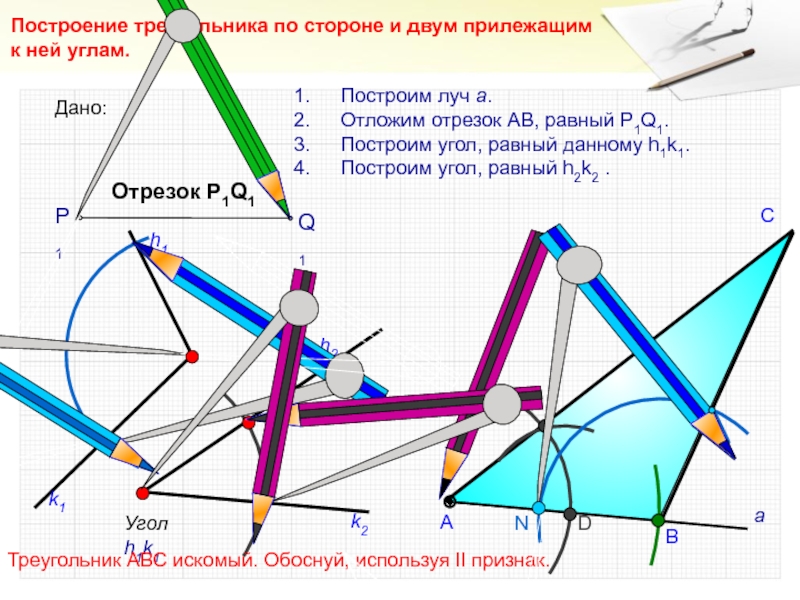
- 21. DСПостроение треугольника по стороне и двум прилежащим
- 22. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
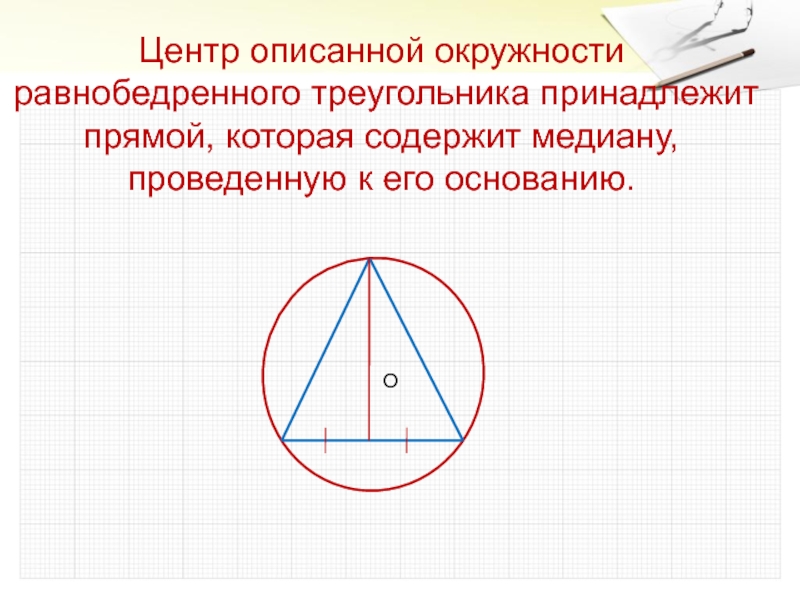
- 23. Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану, проведенную к его основанию.О
- 24. Центр вписанной окружности равнобедренного треугольника принадлежит высоте, проведенной к его основаниюО
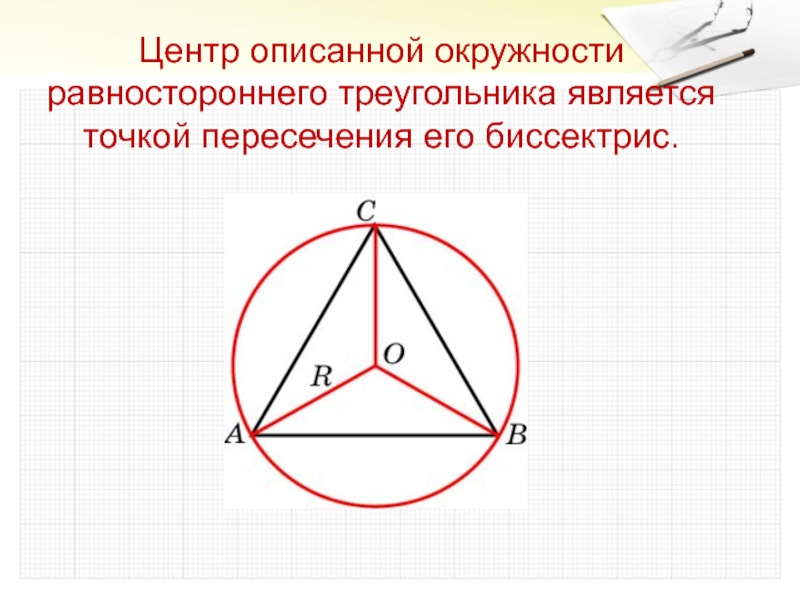
- 25. Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.
- 26. Если центр окружности, описанной около треугольника принадлежит его стороне, то треугольник - прямоугольный
- 27. № 550, 552, 557540, 542Учебник
- 28. Ответьте на вопрос. Мне было интересно узнать о…Легче всего мне было…Трудности вызвало…
- 29. § 21 учить ,№ 553,558Домашнее задание
- 30. 1. Геометрия 7 классы Мерзляк А.Г., М. «Вентана-Граф»2. Анимация http://animashky.ru/index/0-11?25-63. Шаблон http://office.microsoft.com/ru-ru/templates/CT010142747.aspx#ai:TC010362639|Литература и источники
- 31. Скачать презентанцию
Тема урока: Описанная и вписанная окружности треугольника
Слайды и текст этой презентации
Слайд 3Окружность называют описанной около треугольника, если она проходит через все
вершины этого треугольника
Слайд 4На каком рисунке окружность описана около треугольника:
1
2
3
4
5
Если окружность описана около
треугольника,
то треугольник вписан в окружность.
Слайд 5Около любого треугольника можно описать окружность
Заметим, около треугольника можно описать
только одну окружность
Теорема 21.1
Три серединных перпендикуляра сторон треугольника пересекаются в
одной точкеСледствие 1
Следствие 2
Центр окружности, описанной около треугольника, - это точка пересечения серединных перпендикуляров его сторон
Слайд 7На каком рисунке окружность вписана в треугольник:
1
3
4
Если окружность вписана в
треугольник,
то треугольник описан около окружности.
2
5
Слайд 8Заметим, в треугольник можно вписать окружность,
и притом только одну.
О
С1
А1
В1
В любой треугольник можно
вписать окружностьТеорема 21.2
Слайд 9r
Биссектрисы углов треугольника пересекаются в одной точке
Следствие 1
Следствие 2
Центр окружности,
вписанной в треугольник, - это точка пересечения его биссектрис
Слайд 10Радиус окружности вписанной в прямоугольный треугольник, определяется по формуле
где
r – радиус вписанной окружности,
а и b - катеты,
c - гипотенуза
Слайд 12 В геометрии выделяют задачи на построение, которые
можно решить только с помощью двух инструментов: циркуля и линейки
без масштабных делений.Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Слайд 20D
С
Построение треугольника по двум сторонам и углу между ними.
Угол
hk
h
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному.
Отложим
отрезок АС, равный P2Q2.В
А
Треугольник АВС искомый. Обоснуй, используя I признак.
Дано:
Отрезки Р1Q1 и Р2Q2
Q1
P1
P2
Q2
а
k
Слайд 21D
С
Построение треугольника по стороне и двум прилежащим к ней углам.
Угол h1k1
h2
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный
данному h1k1.Построим угол, равный h2k2 .
В
А
Треугольник АВС искомый. Обоснуй, используя II признак.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
h1
k1
N
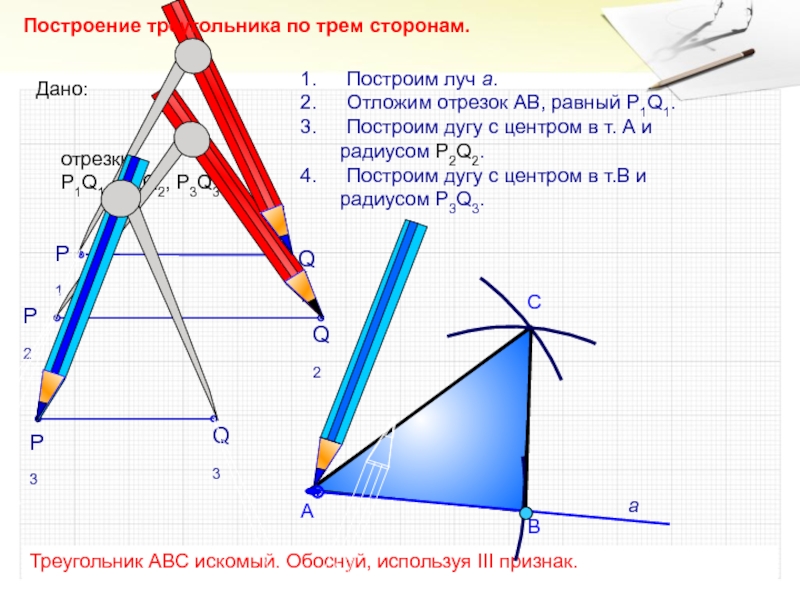
Слайд 22С
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром
в т. А и
радиусом Р2Q2.
Построим дугу
с центром в т.В ирадиусом P3Q3.
В
А
Треугольник АВС искомый. Обоснуй, используя III признак.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
Построение треугольника по трем сторонам.
Слайд 23Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану,
проведенную к его основанию.
О
Слайд 24Центр вписанной окружности равнобедренного треугольника принадлежит высоте, проведенной к его
основанию
О
Слайд 25Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.
Слайд 26Если центр окружности, описанной около треугольника принадлежит его стороне, то
треугольник - прямоугольный
Слайд 301. Геометрия 7 классы Мерзляк А.Г., М. «Вентана-Граф»
2. Анимация http://animashky.ru/index/0-11?25-6
3.
Шаблон http://office.microsoft.com/ru-ru/templates/CT010142747.aspx#ai:TC010362639|
Литература и источники
