ВЯЗКАЯ ЖИДКОСТЬ

диссипации в жидкости. В реальных жидкостях всегда имеет место термодинамическая

необратимость, связанная с наличием эффектов внутреннего трения (вязкости) и переноса тепла(теплопроводности).
Понятно, что полученные ранее уравнения гидродинамики идеальной жидкости не содержат подобных эффектов (это относится только к уравнению Эйлера – уравнение неразрывности сохраняет свою силу).
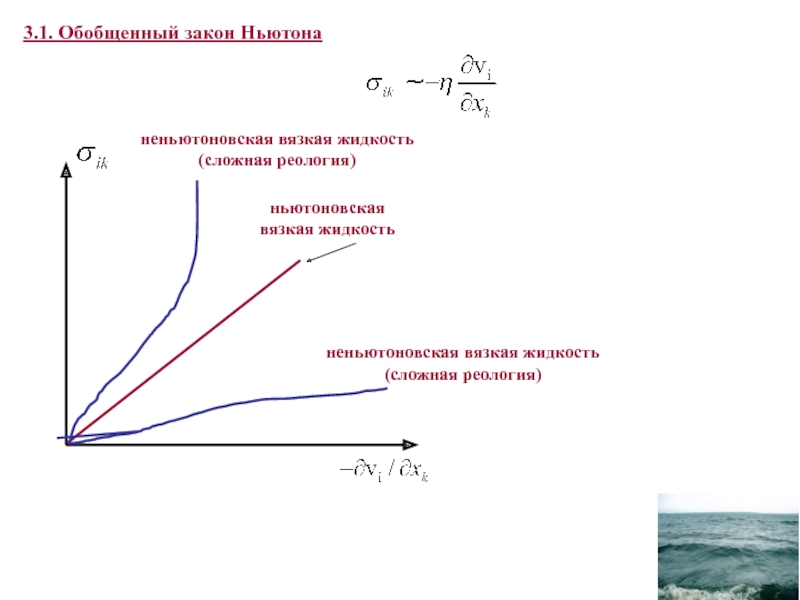
Вывод уравнения для учета потерь от внутреннего трения основывается на следующих соображениях. Наличие внутреннего трения (вязкости) проявляется в наличии дополнительного (необратимого) переноса импульса из мест с большей скоростью в места с меньшей скоростью.
Формально, необходимо дополнить поток импульса для идеальной жидкости необратимым термом, имеющим физический смысл необратимого переноса импульса (диссипации).

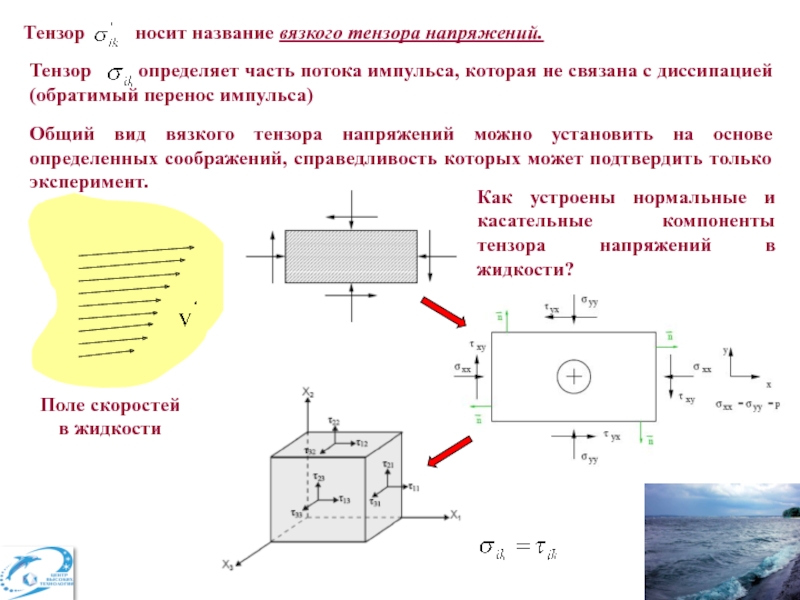
где тензор

- называется тензором напряжений

Тензор определяет часть потока импульса, которая

не связана с диссипацией (обратимый перенос импульса)

Общий вид вязкого тензора напряжений можно установить на основе определенных соображений, справедливость которых может подтвердить только эксперимент.

Поле скоростей в жидкости

Как устроены нормальные и касательные компоненты тензора напряжений в жидкости?

вязкая жидкость (сложная реология)

тензора вязких напряжений, используем следующие соображения:
процессы внутреннего трения имеют

место, если различные участки жидкости движутся с различной скоростью – тензор вязких напряжений должен зависеть от производных скорости жидкости по координатам ;
если градиенты скорости не очень велики, то можно, разложив тензор вязких напряжений в ряд по градиентам скоростей по координатам, оставить только первые члены (обобщенный закон Ньютона для сил трения в жидкости);
члены, не зависящие от градиентов скоростей по координатам должны отсутствовать в тензоре вязких напряжений, поскольку при он должен обращаться в нуль;
тензор вязких напряжений должен быть симметричным, в силу изотропности жидкости, поэтому единственными комбинациями первых производных от скорости жидкости по координатам могут быть суммы

Общий вид тензора второго ранга, который удовлетворяет приведенным выше условиям, является:

(3.1)

от скорости, называются соответственно коэффициентами первой и второй вязкости. Обе

эти величины всегда положительны.
Уравнение движения вязкой жидкости можно получить непосредственно прибавляя в правую часть уравнения Эйлера величины :

Это наиболее общий закон движения вязкой жидкости; величины вообще говоря, могут зависеть от давления и температуры (вместе с последними величинами, коэффициенты вязкости могут меняться от точки к точке, поэтому не вынесены за знак производных).
Если коэффициенты вязкости постоянны вдоль жидкости, то можно получить следующее уравнение из (3.2):

(3.2)

– 1845г. – приведение к современной форме)
Если жидкость несжимаема, тот

уравнение Навье-Стокса сильно упрощается :

Тензор напряжений в несжимаемой жидкости принимает сравнительно простой вид:

Таким образом, процессы диссипации (внутреннего трения) в несжимаемой жидкости описываются всего одним коэффициентом - коэффициентом динамической вязкости. Величина - носит название кинематической вязкости

(3.3)

(3.4)

(3.5)

уравнении Навье-Стокса давление. Применив операцию ротор к обеим частям уравнения

(3.4), получим:

(3.6)

Если распределение скоростей найдено, то давление находится из соотношения (оно получается применением к уравнению (3.4) операции дивергенция:

(3.7)

3.3. Граничные условия для вязкой жидкости

3.3.1. Кинематические граничные условия

На границе с твердым (неподвижным) телом из-за сил межмолекулярного взаимодействия всегда должно быть

Таким образом, и нормальная и касательная компоненты скорости на неподвижной твердой границе должны обращаться в нуль:

На подвижной твердой границе,
движущейся со скоростью:

(3.8)

(3.8а)

(3.8б)

название непроскальзывания (отсутствие скольжения на границе – no slip condition)
В

микро- и наногидродинамике подобное условие может не выполняться !!!

3.3.2. Динамические граничные условия
Для сил на границе с жидкостью должны выполняться условия непрерывности; на границе раздела фаз должны выполняться условия равенства нормальных и касательных напряжений:

1

2

межфазная граница

Общий вид капиллярного (нормального) давления и касательной компоненты тензора напряжений на границе должен устанавливаться отдельно

(3.9)

(3.10)

в плоском канале, одна из стенок которого движется со скоростью

(рис.3.1). Все величины зависят только от y, а скорость направлена везде вдоль оси x.

рис.3.1

Отсюда имеем:

Из уравнения Навье-Стокса следует, что (уравнение неразрывности выполняется автоматически):

При y=0, и при y=h, имеем:

Откуда

найдена из соотношения:
Найдем действующие на стенки силы:
нормальная компонента силы

на стенку равна давлению p=const;
тангенциальная компонента (сила трения при y=0) равна

3.4.2. Течение между двумя плоскостями под действием градиента давления

В этой задаче

Из уравнения Навье-Стокса следует, что (уравнение неразрывности выполняется автоматически):

координаты «y», то в первом уравнении левая часть зависит только

от «x», в правой - только от «y»; следовательно, и правая и левая части – постоянны; таким образом, имеем:

Для скорости получаем:

Из граничных условий при y=0 и y=h, получаем:

Таким образом, имеет место параболический профиль скорости: скорость меняется вдоль толщины жидкости по параболическому закону, достигая максимума в середине канала. Среднее значение скорости по толщине задается градиентом давления:

Сила трения на неподвижную стенку есть:

цилиндрической трубе. Скорость жидкости должна зависеть только от координаты «r»
Уравнение

неразрывности выполняется тождественно, а r-компонента уравнения Навье-Стокса дает . При этом . Здесь
Оператор Лапласа в цилиндрическом уравнении Навье-Стокса есть:

Интегрируя, получаем:

Поскольку скорость везде должна быть конечной, необходимо положить a=0; постоянная b определяется из граничного условия:

закону (пуазейлевский профиль скорости)
При это расход жидкости можно определить из

соотношения:

Общие замечания:
существуют точные решения уравнений Навье-Стокса; их относительно немного (некоторые из них рассмотрены выше для простейших случаев);
существуют так называемые асимптотические методы решения уравнений Навье-Стокса, в которых используются различные разложения решений по малому параметру;
наиболее часто применяемыми в настоящее время являются численные решения, однако для достаточно сложных геометрий и граничных условий даже компьютерное моделирование (CFD) часто приводит к весьма серьезным сложностям в расчетах.

исследованиях гидродинамики вязкой жидкости играют так называемые законы подобия. Можно

показать, что любые стационарные вязкие течения жидкости характеризуются тремя основными размерными параметрами:

Из указанных величин можно составить единственную безразмерную комбинацию типа:

- число Рейнольдса

Если ввести, например, безразмерные координаты , тогда поле скоростей вязкой жидкости можно искать в безразмерной форме:

Таким образом, если числа Рейнольдса для двух видов течений, например, обтекания тел различного размера, равны, то поля скоростей подобны и получаются друг из друга изменением масштаба. Это – так называемый закон подобия Рейнольдса (1883г.)

O. Reynolds
(1842-1912)

(3.11)

(3.12)

силы сопротивления:
3.5.2. Течения при малых числах Рейнольдса
Существенное значение имеют классы

стационарных течений вязкой жидкости при так называемых малых числах Рейнольдса. Если записать стационарное уравнение Навье-Стокса в форме:

тогда справедливы оценки:

Если число Рейнольдса , то нелинейным членом вида можно пренебречь! В этом случае вместо (3.13) имеем линейное уравнение вида:

(3.12а)

(3.13)

(3.14)

Таким образом, при малых числах Рейнольдса уравнение (3.14) вместе с уравнением неразрывности полностью определяет движение вязкой жидкости

жидкости (что эквивалентно задаче об обтекании неподвижного шара потоком жидкости).

Пусть на бесконечности скорость есть .

Для решения этой задачи (задача Стокса, 1851г.) воспользуемся тем обстоятельством, что, если - скорость жидкости, то очевидно выполняется условие:

(причем )

Можно показать, что общий вид решения уравнения Навье-Стокса должен иметь вид:

- единичный вектор в направлении радиуса-вектора

(3.15)

что
Тогда получаем, что
В этом случае уравнение (3.14) принимает вид:
Или
(3.16)
Отсюда
(3.17)
В уравнении

(3.17) постоянную можно положить равной нулю.

Таким образом, получаем в соответствующих координатах уравнение типа:

(3.18)

решение Стокса
(3.20)
В сферических координатах получаем для скорости
(3.21)

со стороны жидкости, действующую на шар (или, силу сопротивления, которую

испытывает шар в жидкости). Общее выражение для такой силы, действующей на единицу поверхности, есть:

- давление жидкости на бесконечности

Поскольку такая сила действует только вдоль направления , то введя полярные координаты (см. рисунок) и проектируя эту силу на направление скорости, получим (S – поверхность шара):

Подставляя выражения для компонент скорости в:

Получаем:

силы сопротивления шара стационарном потоке вязкой жидкости:
- формула Стокса (1851г.)
Поправки

к формуле Стокса

На самом деле (3.14) – не точно отражает ситуацию. Более строгий подход (Озеен, 1910г.) показывает, что необходимо пользоваться уравнением вида

(3.22)

(3.23)

Из этого уравнения можно получить поправки Озеена к формуле Стокса

(3.24)

- формула Озеена (1910г.)