Слайд 1Выбор проектных решений
методом анализа иерархий
Слайд 2Задача принятия решений
Х={А, K, S, I}
А – множество альтернатив (зависит
от имеющейся базы знаний, новизны задачи);
K – множество критериев
оценки альтернатив (зависит от степени детализации задачи и требуемого качества ее решения);
S – метод поиска (вывода) решения:
способ выбора альтернатив, определяемый структурой предпочтений ЛПР;
метод (модель) оптимизации, обусловливающий способ агрегирования критериев.
I – уровень информации
Слайд 3Подход к принятию решений
Классический.
Каждый вариант решения Х оценивается неотрицательной
действительно-значной функцией выигрыша g(x).
Хопт=max g(x).
Применяется в детерминированной среде и
условиях риска.
Поведенческий.
Множество последствий каждого варианта p(x) сравнивается с множеством допустимых последствий при решении данной проблемы pд(x).
Применяется в условиях неопределенности
Слайд 4Модель принятия решений
Модель принятия решений – процедура оценивания, помогающая делать
выбор между альтернативами.
По числу целей (способу описания объекта):
одноцелевые (однокритериальные) модели
(модели «прибыль – издержки», «эффективность – затраты»)
многоцелевые (многокритериальные) модели (многомерные функции полезности, модели сравнения вариантов, основанные на обработке экспертной информации)
Слайд 5Методы классического подхода выбора альтернатив
Метод теории полезности
Метод взвешенной суммы оценок
критериев
Метод анализа иерархий
Слайд 6Метод построения многомерной функции полезности
Провести опрос экспертов.
Построить одномерные функции полезности.
Провести
ранжирование возможных исходов без взаимного сравнения альтернатив.
Построить многомерную функцию полезности
как аддитивную или мультипликативную комбинацию одномерных функций.
Допущение: критерии являются взаимно независимыми по полезности.
Достоинство: возможность оценки любого количества альтернативных вариантов с использованием полученной функции.
Недостатки:
необходимость привлечения значительных объемов информации;
высокая трудоемкость;
исходная информация должна быть устойчивой.
Слайд 7Метод взвешенной суммы оценок критериев
Определяется перечень альтернатив и перечень критериев.
Каждой
альтернативе дается балльная оценка по каждому из критериев.
Критериям приписываются
количественные веса, характеризующие их сравнительную важность.
Определяется ценность альтернативы путем умножения весов на критериальные оценки с последующим суммированием.
Выбирается альтернатива с наибольшим показателем ценности.
Достоинство: простота и удобство
Недостаток: отсутствие научного обоснования при определении весов критериев и альтернатив.
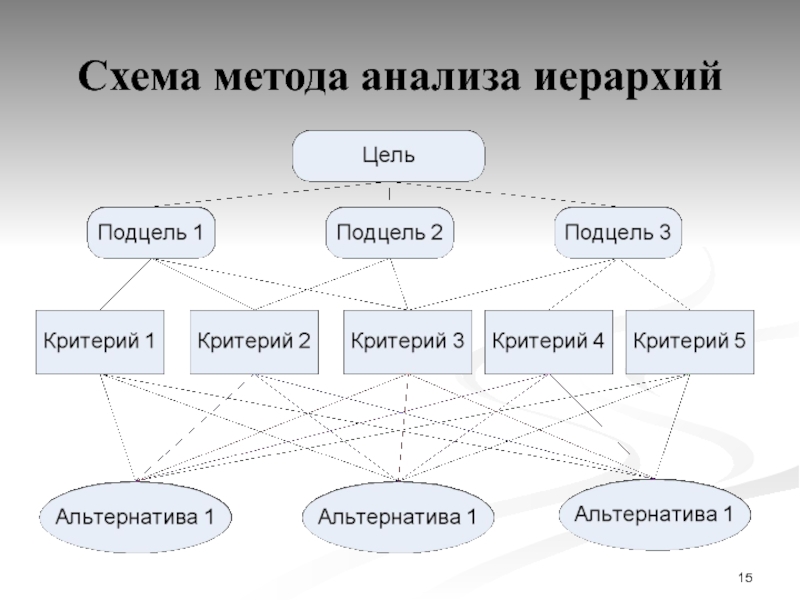
Слайд 8Метод анализа иерархий
Декомпозиция проблемы.
Обработка последовательности суждений эксперта по парным сравнениям
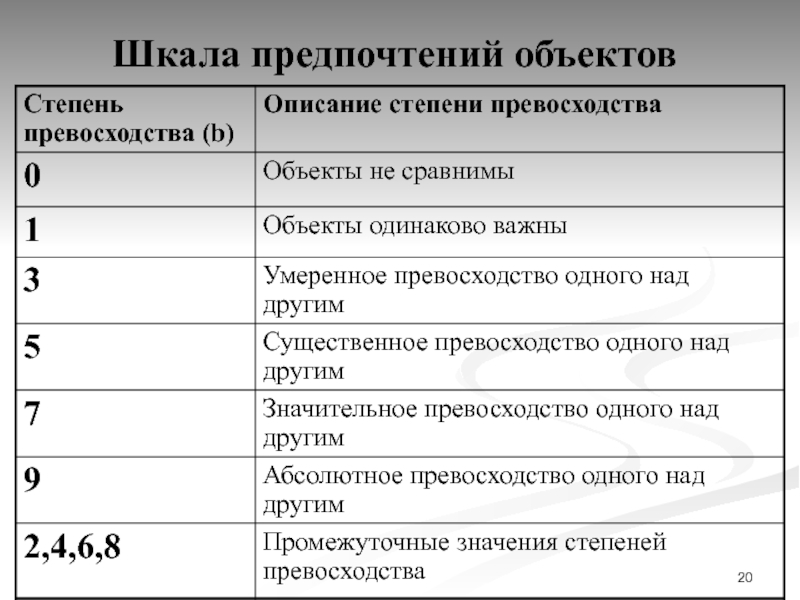
в соответствии с заданной шкалой предпочтений.
Ранжирование критериев.
Ранжирование альтернатив по
каждому из критериев.
Определение оптимальной альтернативы по совокупности критериев с учетом их весов.
Достоинства: простота применения и соответствие интуитивным представлениям.
Недостаток: ограничение на количество одновременно сравниваемых альтернатив (5-9)
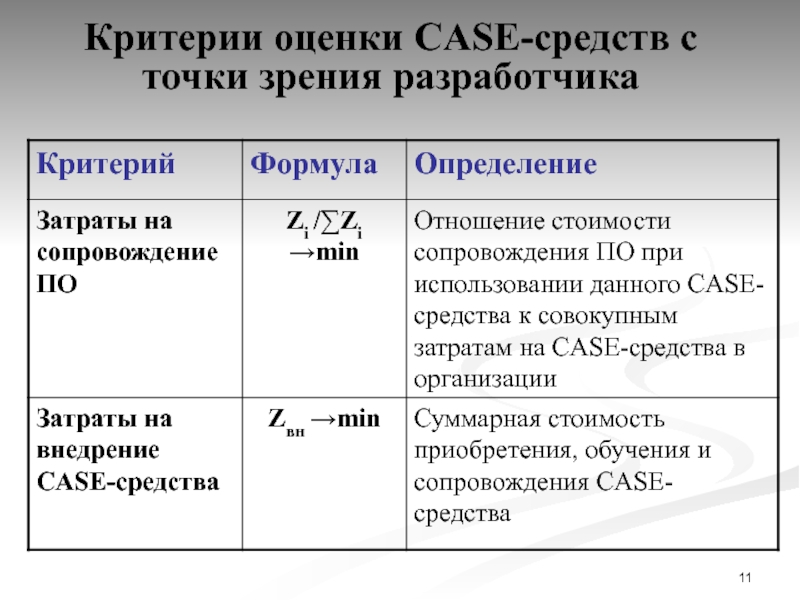
Слайд 10Критерии оценки CASE-средств с точки зрения разработчика
Слайд 11Критерии оценки CASE-средств с точки зрения разработчика
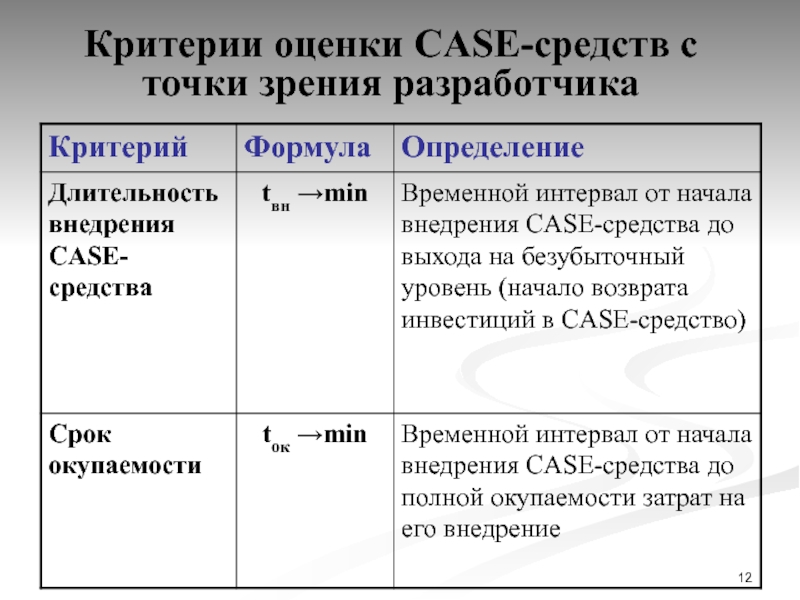
Слайд 12Критерии оценки CASE-средств с точки зрения разработчика
Слайд 13Критерии оценки с точки зрения заказчика
Удобство использования;
степень согласованности с
существующими в организации бизнес-процессами;
степень интеграции с другими программными средствами;
требуемая
квалификация пользователей.
Слайд 14Источники информации
техническая документация поставщика;
доступные данные о реальных внедрениях;
результаты выполнения пилотных
проектов;
материалы конференций и семинаров, проводимых поставщиками и пользователями CASE-средств и
ТПР.
Слайд 17Алгоритм МАИ
Определение иерархии целей.
Установление приоритетов критериев методом попарного сравнения.
Установление приоритетов
альтернатив по каждому критерию.
Определение глобального приоритета альтернатив.
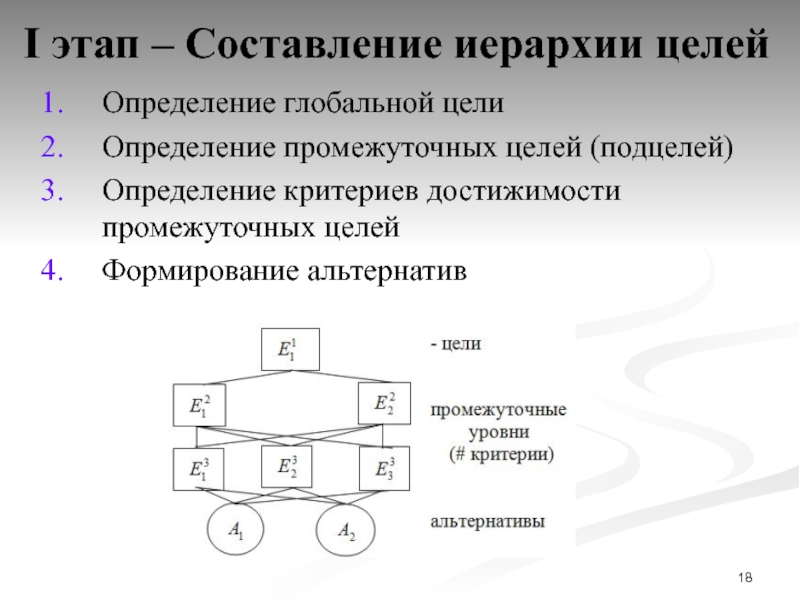
Слайд 18I этап – Составление иерархии целей
Определение глобальной цели
Определение промежуточных целей
(подцелей)
Определение критериев достижимости промежуточных целей
Формирование альтернатив
Слайд 19II этап – Установление приоритетов критериев
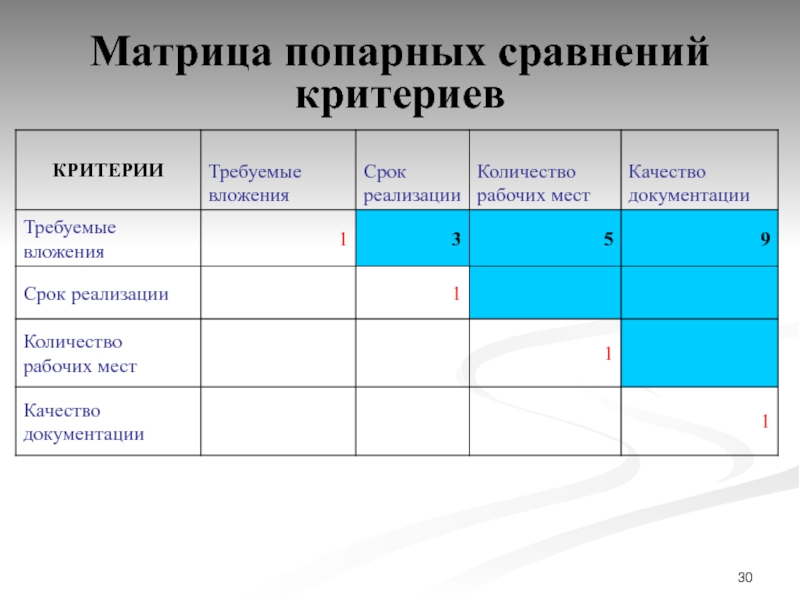
Формирование матрицы попарных сравнений критериев
с использованием шкалы предпочтений одного сравниваемого объекта другому.
Ранжирование критериев
Оценка компонент
собственного вектора каждого критерия
Нормализация оценок
Оценка согласованности матрицы
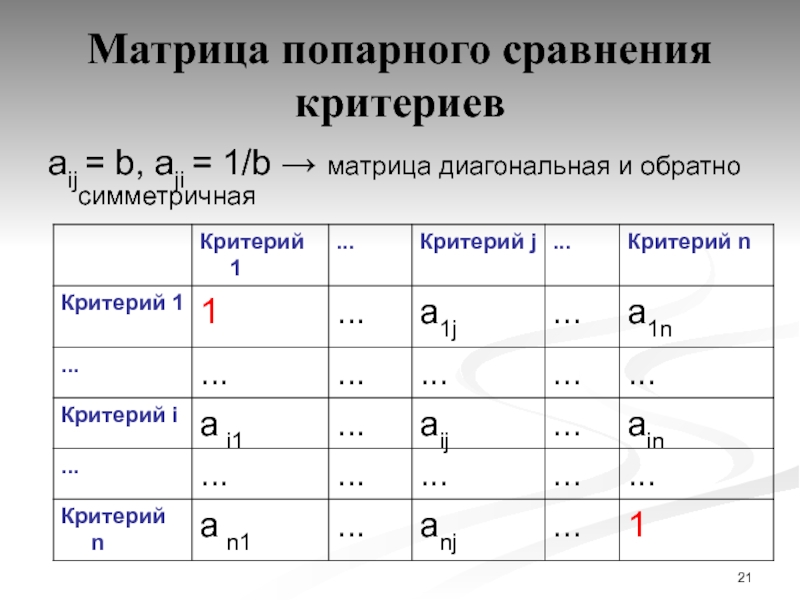
Слайд 21Матрица попарного сравнения критериев
аij = b, аji = 1/b →
матрица диагональная и обратно симметричная
Слайд 22
Если элемент E1 доминирует над элементом E2, то клетка матрицы,
соответствующая строке E1 и столбцу E2 заполняется целым числом, а
клетка, соответствующая строке E2 и столбцу E1 заполняется обратным к нему числом.
Данная матрица называется матрицей парных сравнений.
Пример составления матрицы парных сравнений
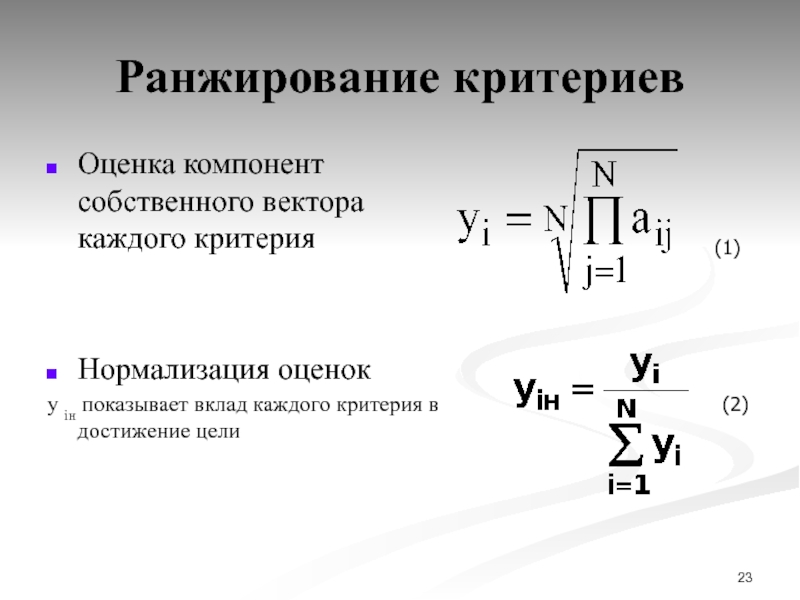
Слайд 23Ранжирование критериев
Оценка компонент собственного вектора каждого критерия
Нормализация оценок
y iн
показывает вклад каждого критерия в достижение цели
(1)
(2)
Слайд 24Оценка согласованности матрицы
Вычисление максимального собственного числа матрицы (λmax)
Вычисление индекса согласованности
(ИС)
Вычисление оценки согласованности (ОС )
ОС = ИС/СC
ОС ≤ 0,1 матрица
согласованна
0,1<ОС ≤ 0,2 согласованность матрицы приемлема
ОС > 0,2 согласованность матрицы не приемлема
Значения случайной согласованности (СС)
(3)
(4)
(5)
(6)
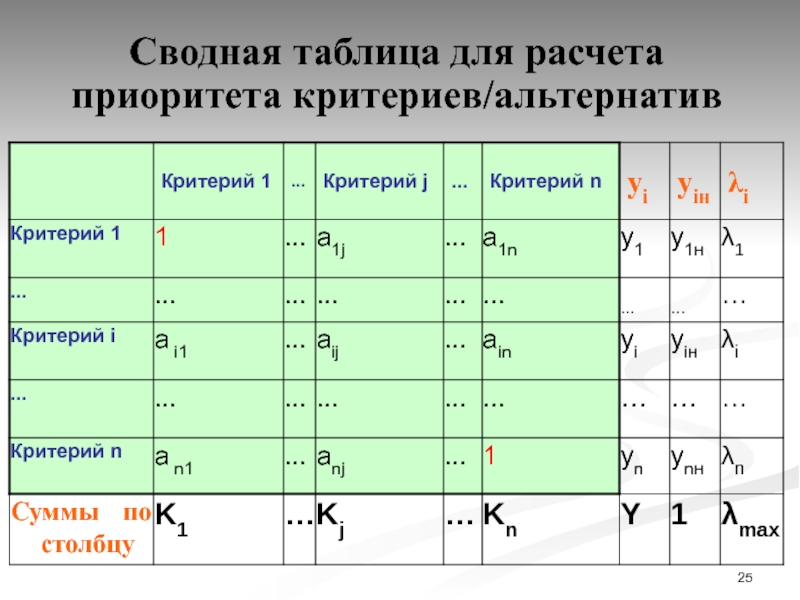
Слайд 25Сводная таблица для расчета приоритета критериев/альтернатив
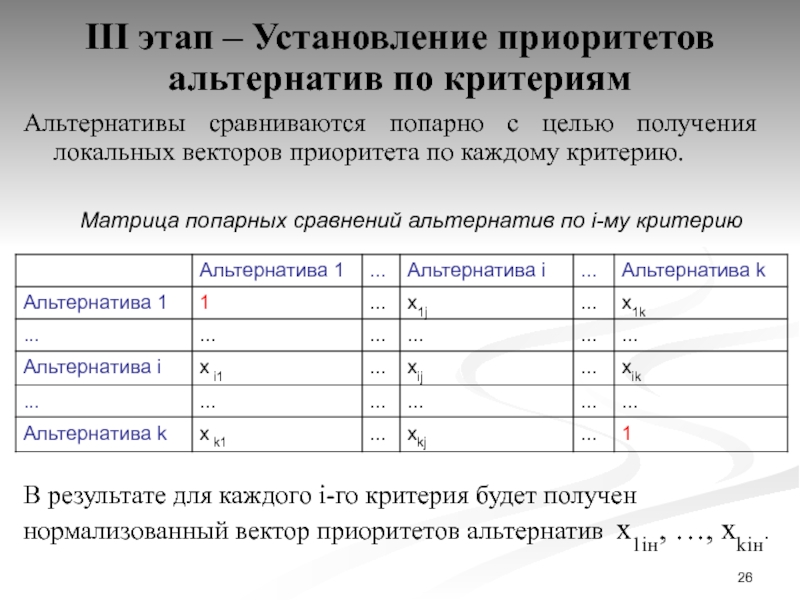
Слайд 26III этап – Установление приоритетов альтернатив по критериям
Альтернативы сравниваются попарно
с целью получения локальных векторов приоритета по каждому критерию.
Матрица попарных
сравнений альтернатив по i-му критерию
В результате для каждого i-го критерия будет получен нормализованный вектор приоритетов альтернатив x1iн, …, хkiн.
Слайд 27IV этап – Определение глобального приоритета альтернатив
Aopt=max Ai
(7)
(8)
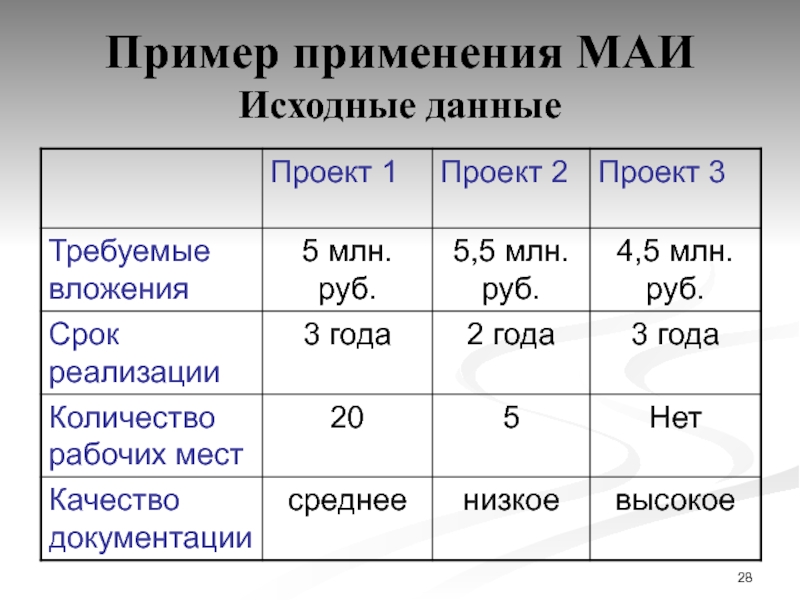
Слайд 28Пример применения МАИ Исходные данные
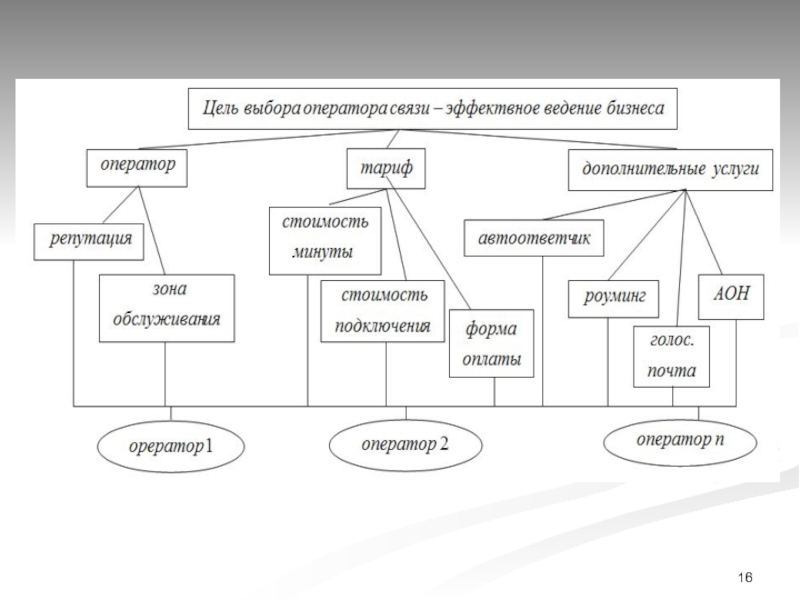
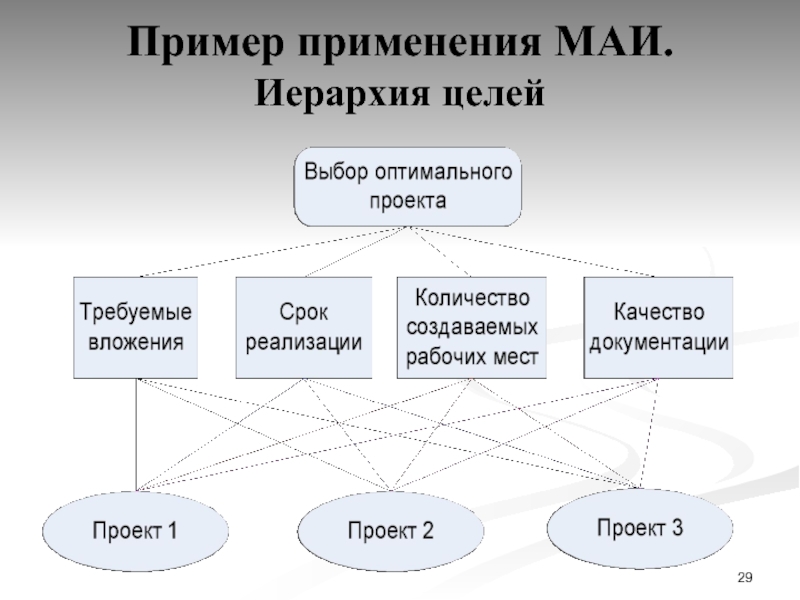
Слайд 29Пример применения МАИ.
Иерархия целей
Слайд 30Матрица попарных сравнений критериев
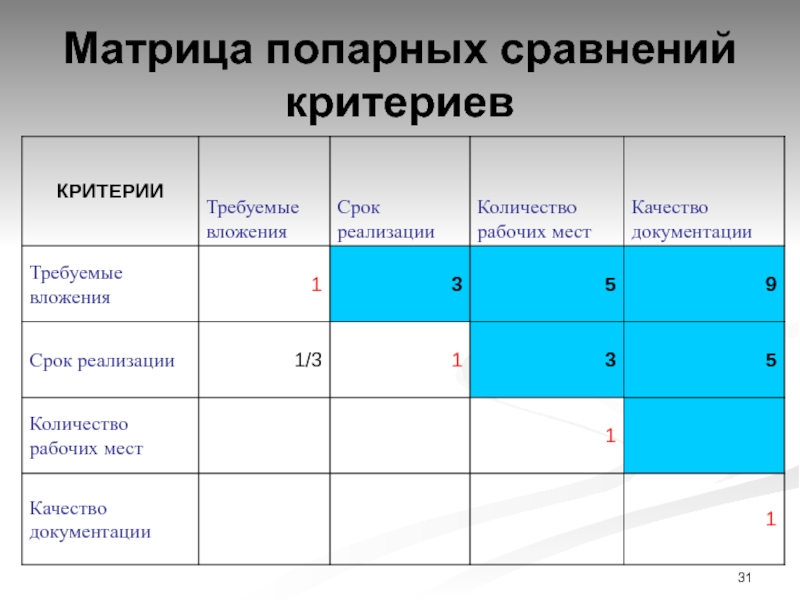
Слайд 31Матрица попарных сравнений критериев
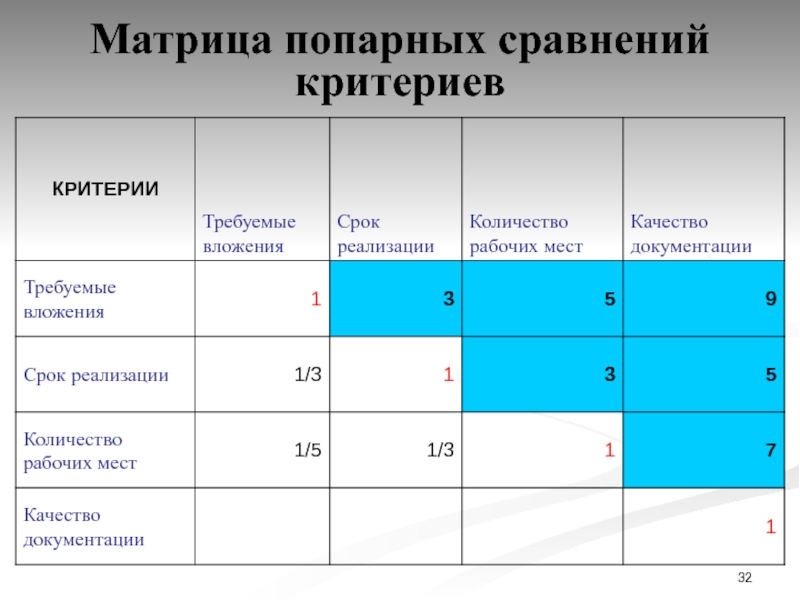
Слайд 32Матрица попарных сравнений критериев
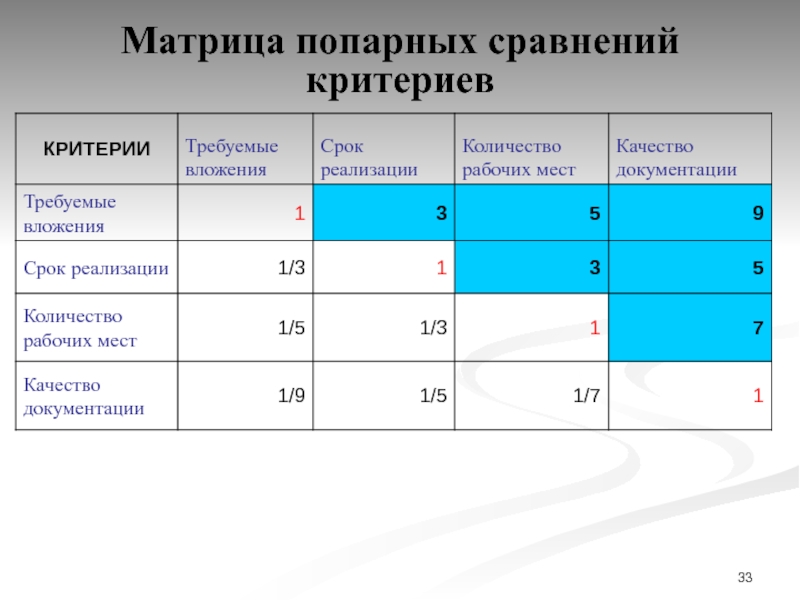
Слайд 33Матрица попарных сравнений критериев
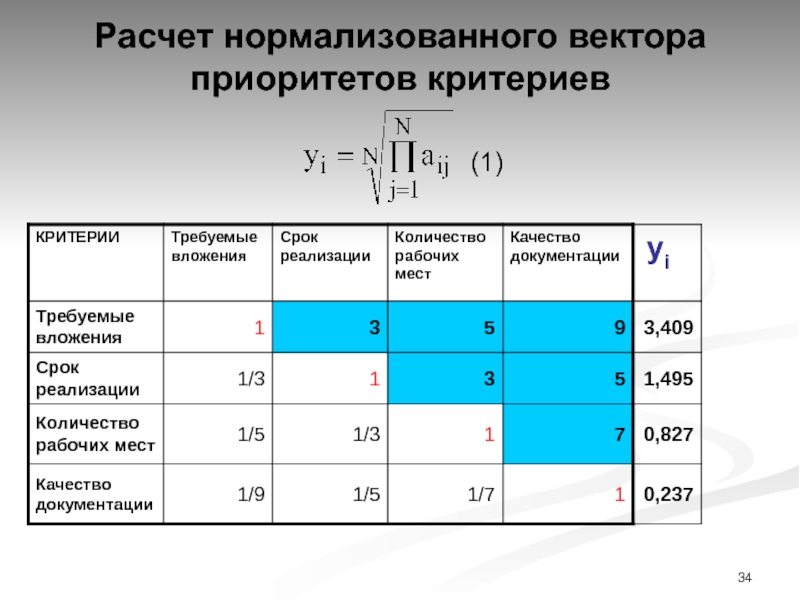
Слайд 34Расчет нормализованного вектора приоритетов критериев
(1)
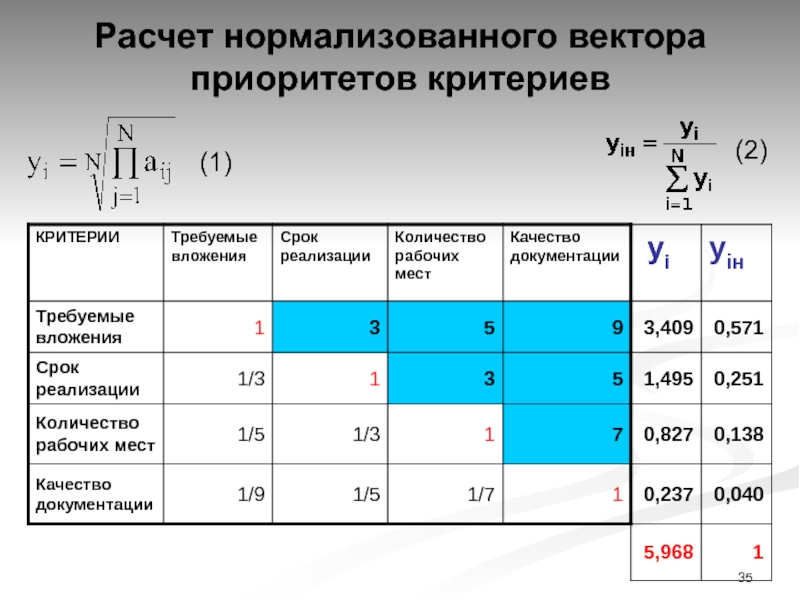
Слайд 35Расчет нормализованного вектора приоритетов критериев
(1)
(2)
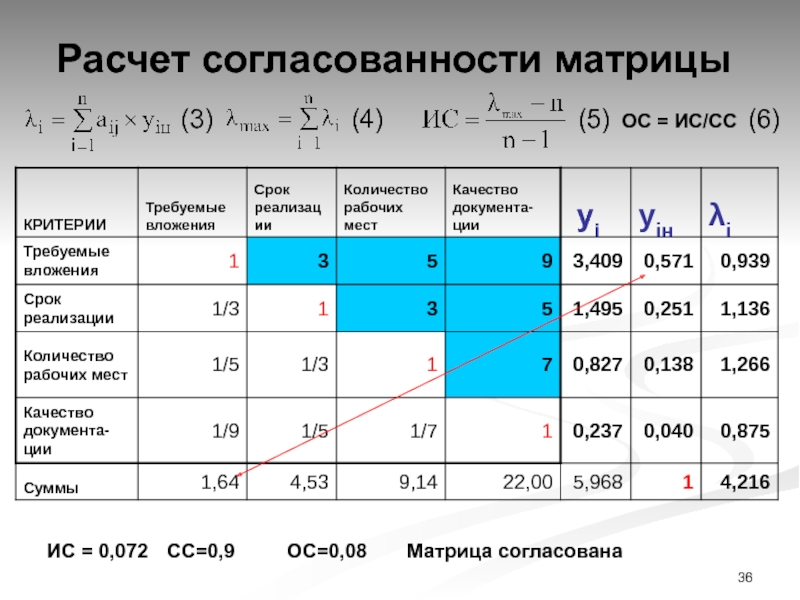
Слайд 36Расчет согласованности матрицы
ОС = ИС/СС
ИС = 0,072 СС=0,9 ОС=0,08 Матрица согласована
(3)
(4)
(5)
(6)
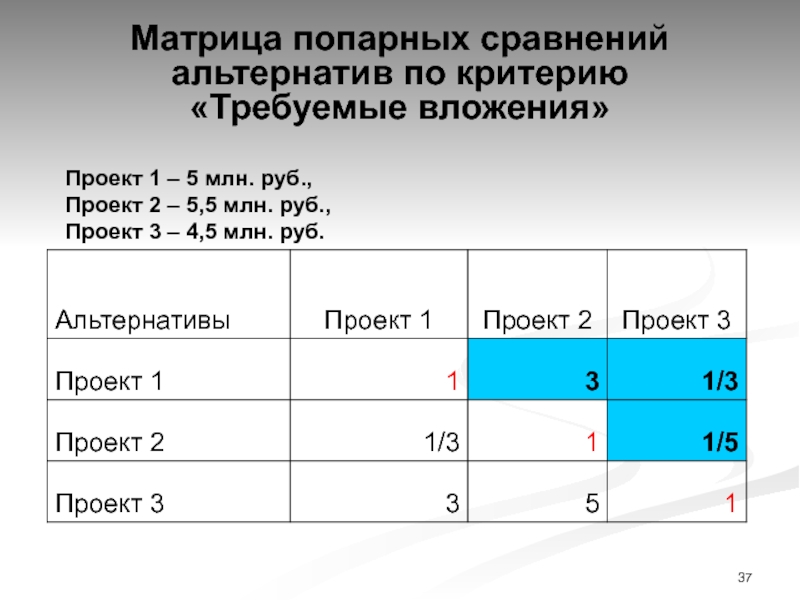
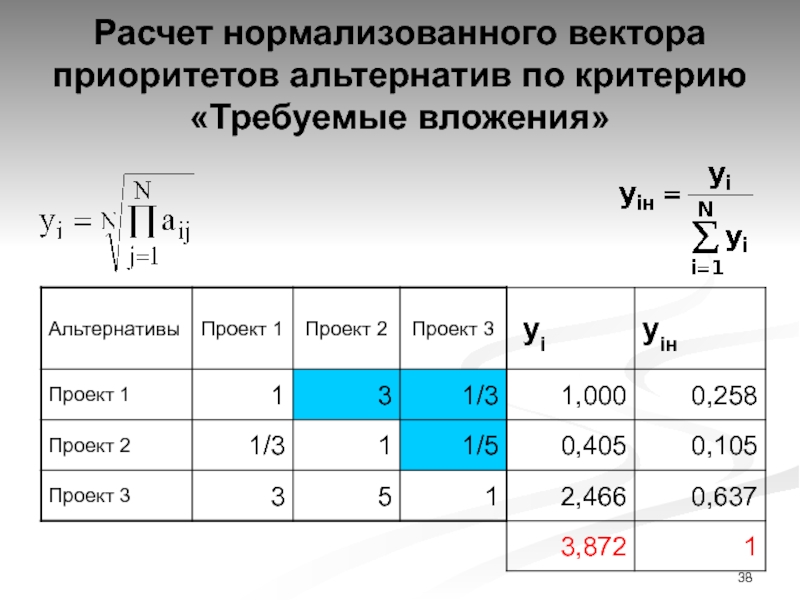
Слайд 37Матрица попарных сравнений альтернатив по критерию
«Требуемые вложения»
Проект 1 –
5 млн. руб.,
Проект 2 – 5,5 млн. руб.,
Проект
3 – 4,5 млн. руб.
Слайд 38Расчет нормализованного вектора приоритетов альтернатив по критерию «Требуемые вложения»
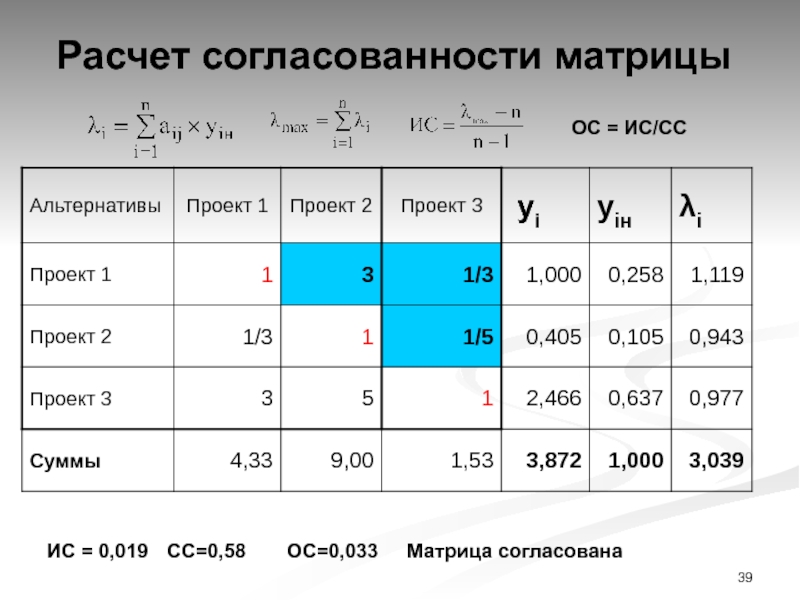
Слайд 39Расчет согласованности матрицы
ОС = ИС/СС
ИС = 0,019 СС=0,58 ОС=0,033 Матрица согласована
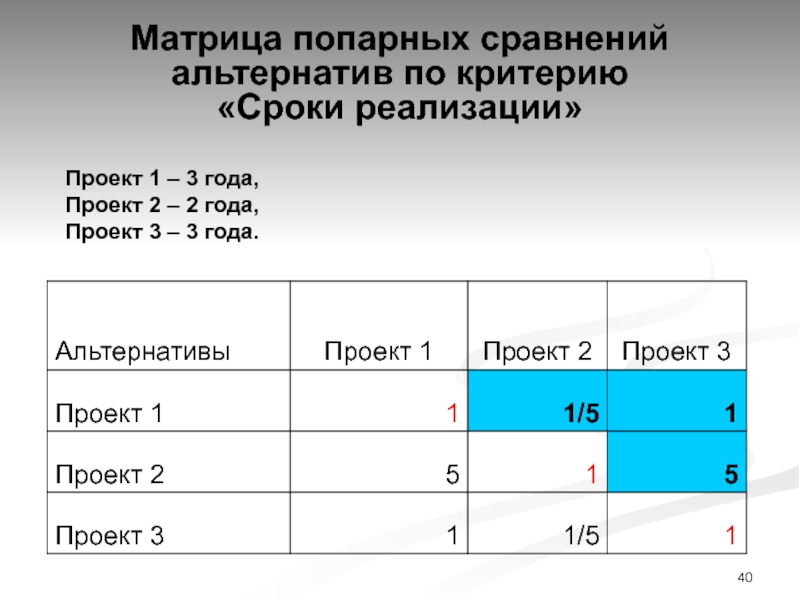
Слайд 40Матрица попарных сравнений альтернатив по критерию
«Сроки реализации»
Проект 1 –
3 года,
Проект 2 – 2 года,
Проект 3 –
3 года.
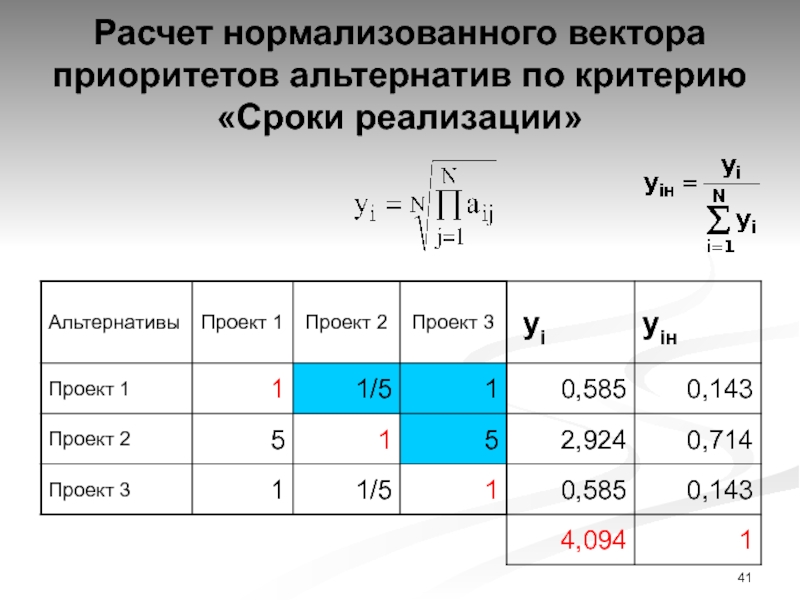
Слайд 41Расчет нормализованного вектора приоритетов альтернатив по критерию «Сроки реализации»
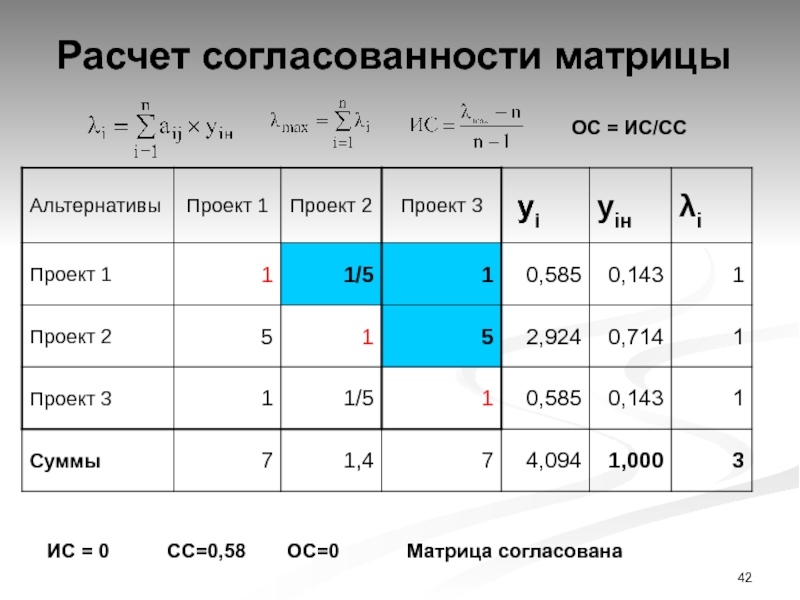
Слайд 42Расчет согласованности матрицы
ОС = ИС/СС
ИС = 0 СС=0,58 ОС=0 Матрица согласована
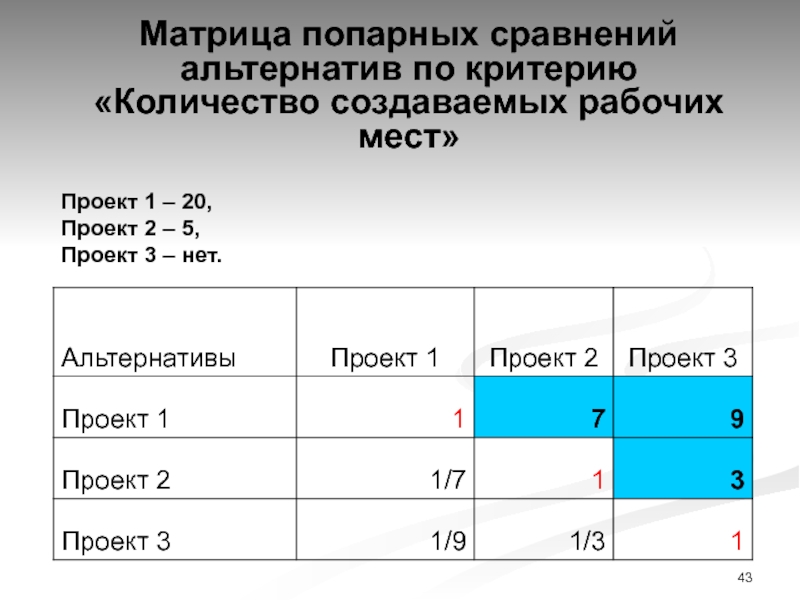
Слайд 43Матрица попарных сравнений альтернатив по критерию
«Количество создаваемых рабочих мест»
Проект
1 – 20,
Проект 2 – 5,
Проект 3 –
нет.
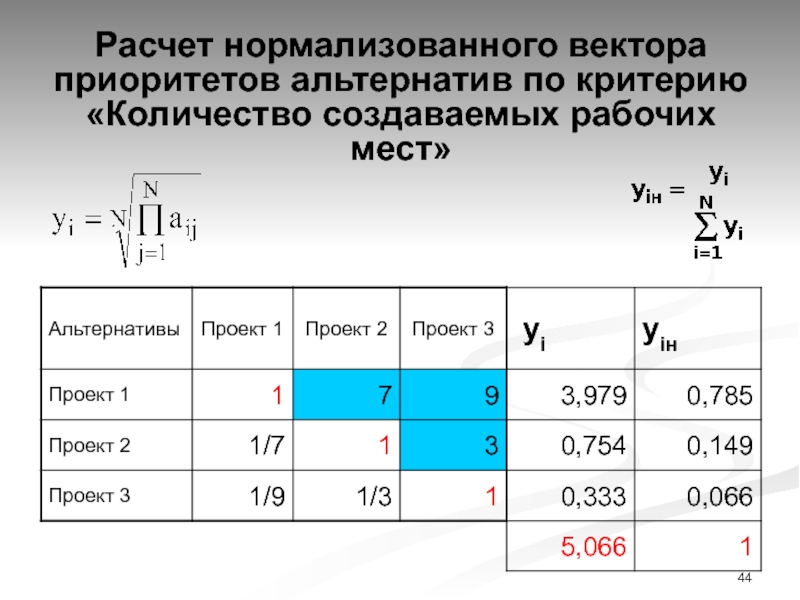
Слайд 44Расчет нормализованного вектора приоритетов альтернатив по критерию «Количество создаваемых рабочих
мест»
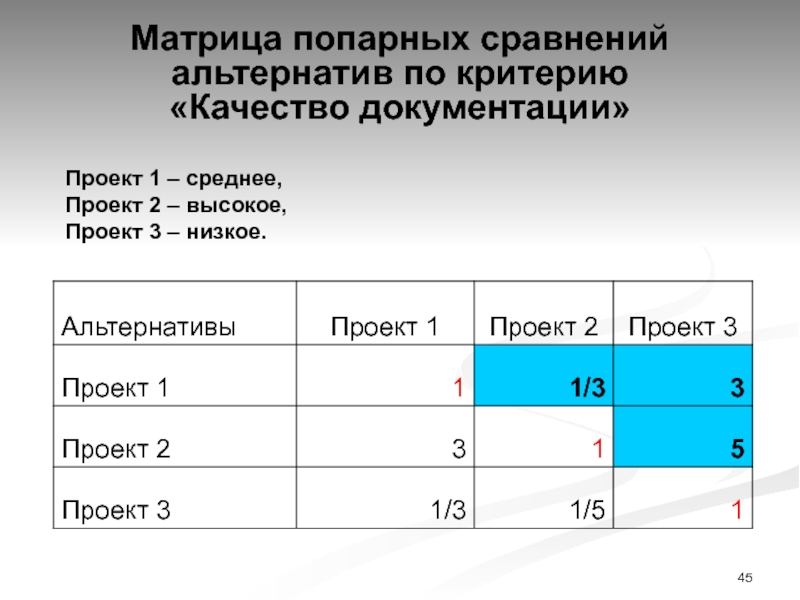
Слайд 45Матрица попарных сравнений альтернатив по критерию
«Качество документации»
Проект 1 –
среднее,
Проект 2 – высокое,
Проект 3 – низкое.
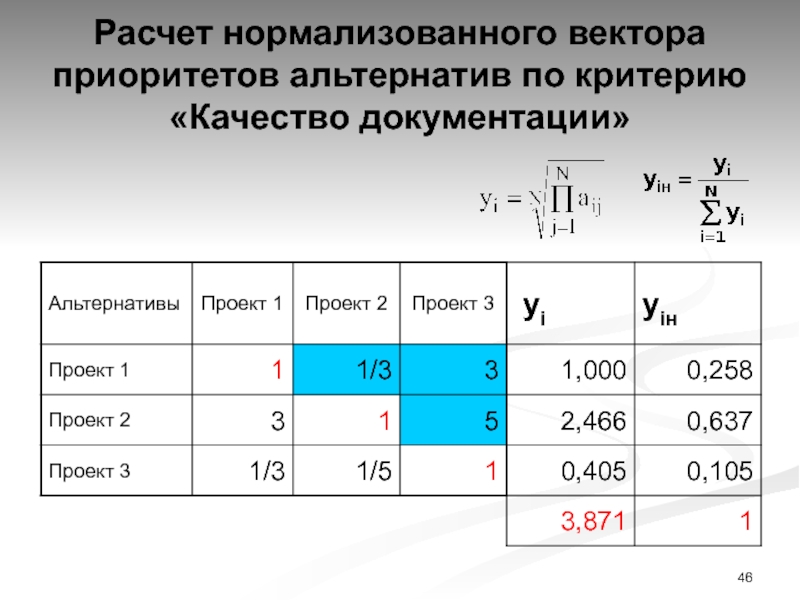
Слайд 46Расчет нормализованного вектора приоритетов альтернатив по критерию «Качество документации»
Слайд 47Расчет глобальных приоритетов
Aopt=max Ai