Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное положение прямой и плоскости
Содержание
- 1. Взаимное положение прямой и плоскости
- 2. План лекции
- 3. 1. Параллельность прямой и плоскостиПрямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей в заданной плоскости.
- 4. XА2В2А1В1С2С1Задача. Через точку М провести прямую, параллельную
- 5. 2. Пересечение прямой и плоскостиЗадачи на определение пересечения (общих элементов) заданных поверхностей называются позиционными.
- 6. 2. Пересечение прямой и
- 7. XА2В2А1В1С2С1Задача. Определить точку пересечения прямой (АВ) и
- 8. 3. Параллельность двух плоскостейДве плоскости параллельны,
- 9. XА2В2А1В1С2С1Задача. Через точку М провести плоскость, параллельную
- 10. Замечание. Если плоскости параллельны, то их одноименные
- 11. 4. Пересечение двух плоскостей
- 12. XА2В2А1В1С2С1Задача. Определить точку пересечения плоскостей {ΔАВС} и
- 13. XА2В2А1В1С2С1Задача. Определить точку пересечения плоскостей {ΔАВС} и
- 14. E 4. Пересечение плоскостейАлгоритм решения:
- 15. XА2В2А1В1С2С1Задача. Определить линию пересечения двух плоскостей. 4.
- 16. доценты кафедры «Начертательная геометрия, инженерная и компьютерная
- 17. Скачать презентанцию
План лекции
Слайды и текст этой презентации
Слайд 31. Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна
какой-либо прямой, принадлежащей в заданной плоскости.
Слайд 4
X
А2
В2
А1
В1
С2
С1
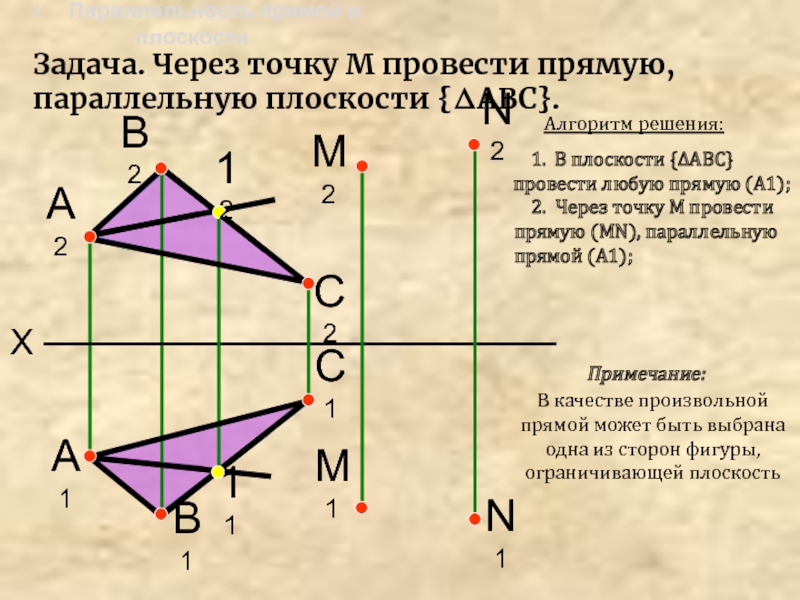
Задача. Через точку М провести прямую, параллельную плоскости {ΔАВС}.
М2
М1
1.
Параллельность прямой и плоскости
Алгоритм решения:
1. В
плоскости {ΔАВС} провести любую прямую (А1);11
12
2. Через точку М провести прямую (МN), параллельную прямой (А1);
N1
N2
Примечание:
В качестве произвольной прямой может быть выбрана одна из сторон фигуры, ограничивающей плоскость
Слайд 52. Пересечение прямой и плоскости
Задачи на определение пересечения (общих элементов)
заданных поверхностей называются позиционными.
Слайд 6 2. Пересечение прямой и плоскости
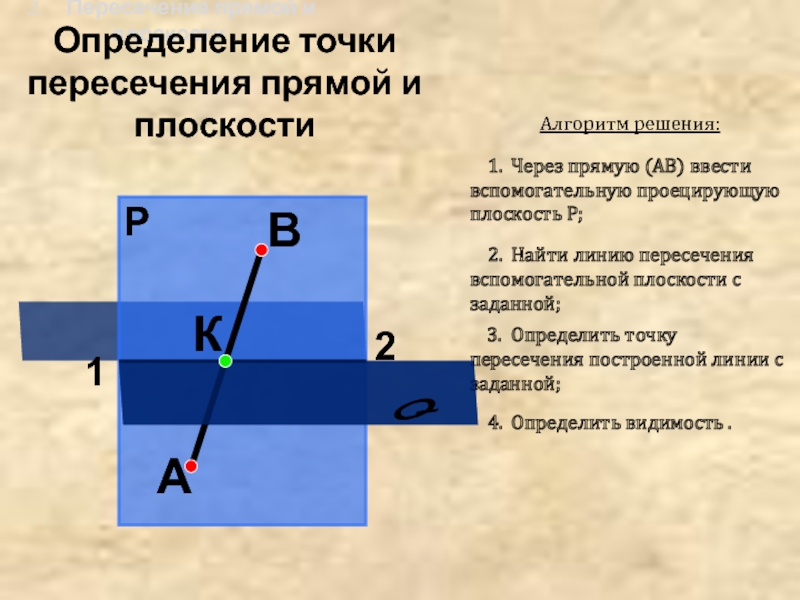
Алгоритм решения:
1. Через прямую (АВ) ввести вспомогательную проецирующую плоскость P;
2. Найти линию пересечения вспомогательной плоскости с заданной;Определение точки пересечения прямой и плоскости
P
В
А
1
2
3. Определить точку пересечения построенной линии с заданной;
К
4. Определить видимость .
Q
Слайд 7
X
А2
В2
А1
В1
С2
С1
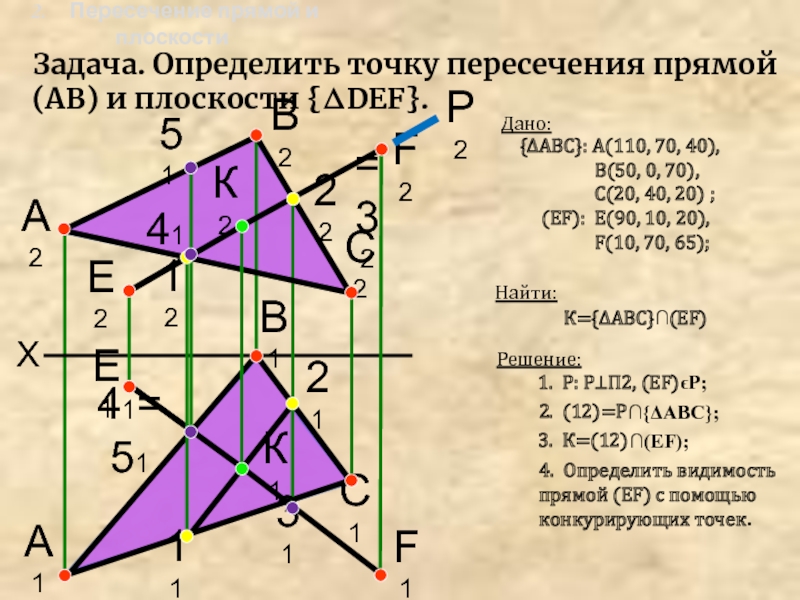
Задача. Определить точку пересечения прямой (АВ) и плоскости {ΔDEF}.
E2
E1
2.
Пересечение прямой и плоскости
Дано:
{ΔАВС}: А(110, 70, 40),
В(50, 0, 70), С(20, 40, 20) ;
(EF): E(90, 10, 20),
F(10, 70, 65);
21
22
1. Р: P⊥П2, (EF)ϵP;
F1
F2
11
12
К1
К2
Найти:
К={ΔАВС}∩(EF)
Решение:
Р2
2. (12)=Р∩{ΔАВС};
3. К=(12)∩(EF);
4. Определить видимость прямой (EF) с помощью конкурирующих точек.
=32
31
41=51
51
41
Слайд 83. Параллельность двух плоскостей
Две плоскости параллельны, если две пересекающиеся
прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.
Слайд 9
X
А2
В2
А1
В1
С2
С1
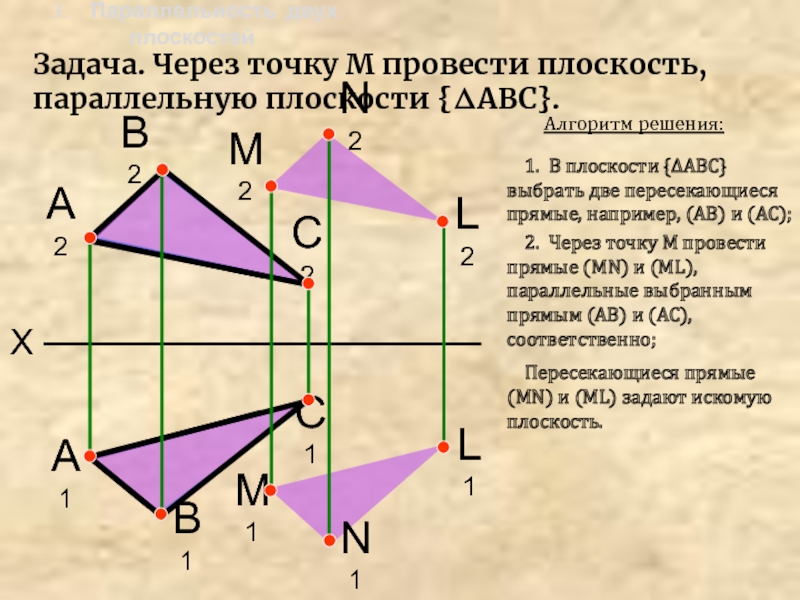
Задача. Через точку М провести плоскость, параллельную плоскости {ΔАВС}.
М2
М1
3.
Параллельность двух плоскостей
Алгоритм решения:
1. В плоскости
{ΔАВС} выбрать две пересекающиеся прямые, например, (АВ) и (АС); 2. Через точку М провести прямые (МN) и (ML), параллельные выбранным прямым (АВ) и (АС), соответственно;
N1
N2
Пересекающиеся прямые (МN) и (ML) задают искомую плоскость.
L1
L2
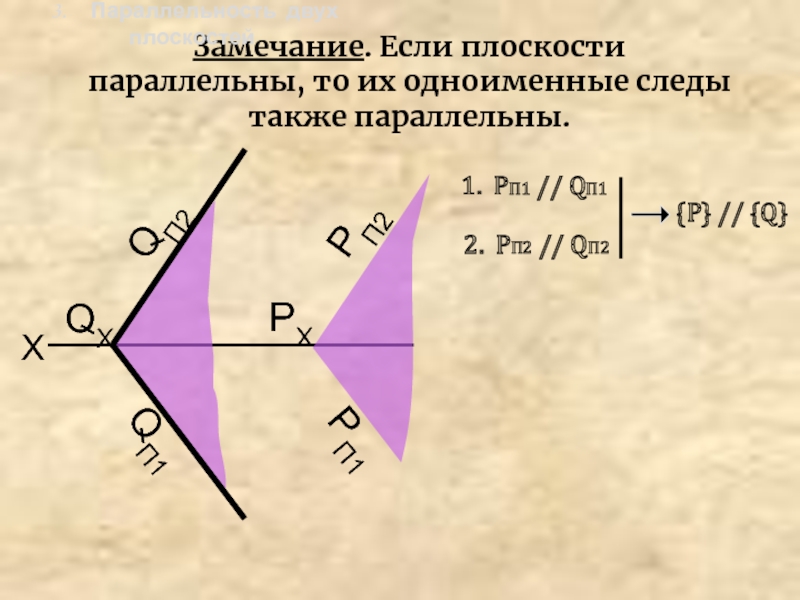
Слайд 10Замечание. Если плоскости параллельны, то их одноименные следы также параллельны.
3. Параллельность двух плоскостей
1. РП1 //
QП12. РП2 // QП2
{Р} // {Q}
X
QП2
QX
QП1
РП2
РX
РП1
Слайд 12
X
А2
В2
А1
В1
С2
С1
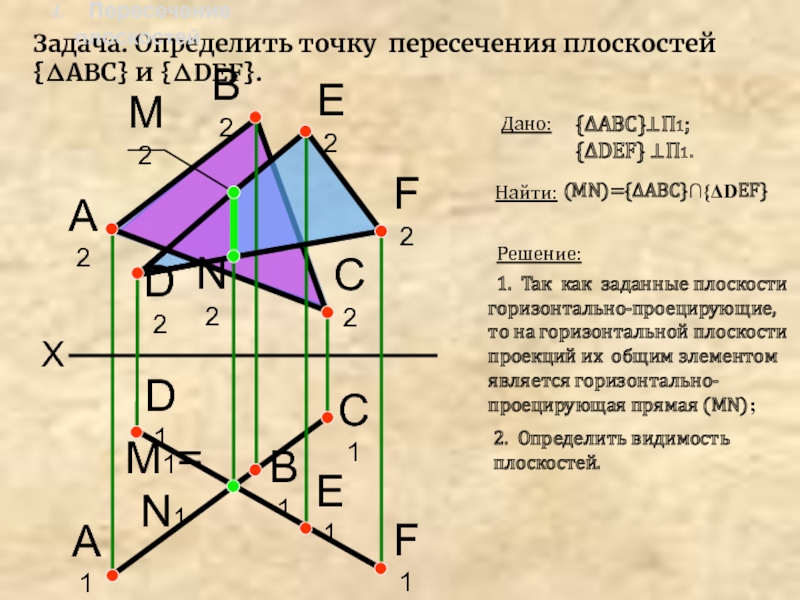
Задача. Определить точку пересечения плоскостей {ΔАВС} и {ΔDEF}.
4.
Пересечение плоскостей
Дано:
{ΔАВС}⊥П1;
{ΔDEF} ⊥П1.
1. Так как заданные плоскости горизонтально-проецирующие,
то на горизонтальной плоскости проекций их общим элементом является горизонтально-проецирующая прямая (MN);D1
D2
M1=N1
M2
Найти:
(MN)={ΔАВС}∩{ΔDEF}
Решение:
2. Определить видимость плоскостей.
E1
E2
F1
F2
N2
Слайд 13
X
А2
В2
А1
В1
С2
С1
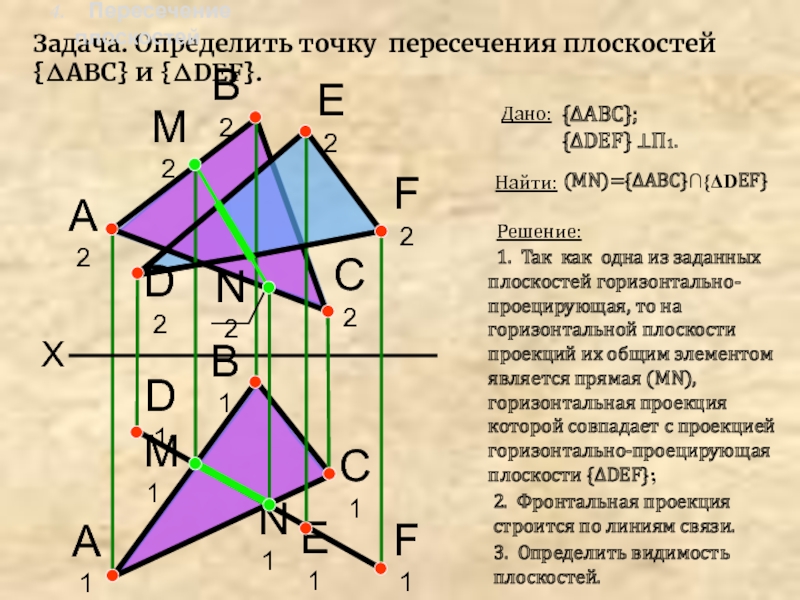
Задача. Определить точку пересечения плоскостей {ΔАВС} и {ΔDEF}.
4.
Пересечение плоскостей
Дано:
{ΔАВС};
{ΔDEF} ⊥П1.
1. Так как одна из
заданных плоскостей горизонтально-проецирующая, то на горизонтальной плоскости проекций их общим элементом является прямая (MN), горизонтальная проекция которой совпадает с проекцией горизонтально-проецирующая плоскости {ΔDEF};D1
D2
M1
M2
Найти:
(MN)={ΔАВС}∩{ΔDEF}
Решение:
3. Определить видимость плоскостей.
E1
E2
F1
F2
N2
N1
2. Фронтальная проекция строится по линиям связи.
Слайд 14
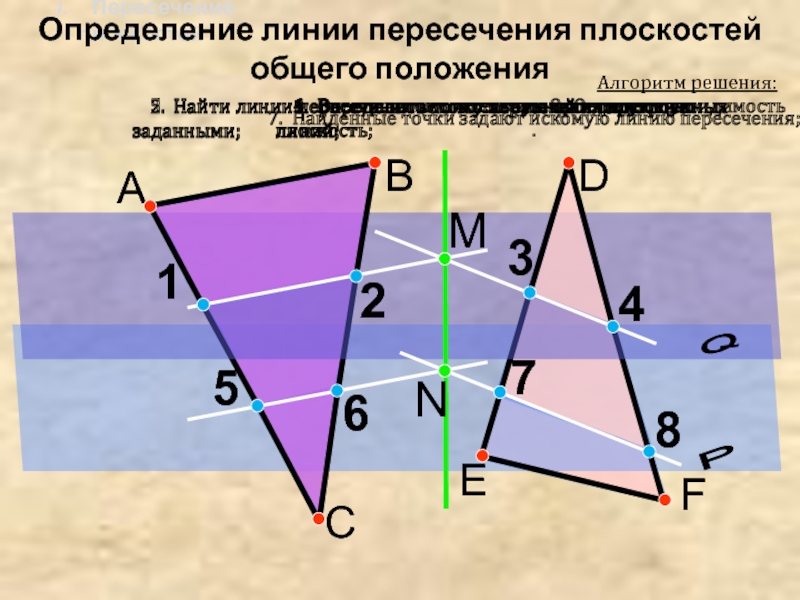
E
4. Пересечение плоскостей
Алгоритм решения:
1. Ввести
вспомогательную проецирующую плоскость;
2. Найти линии пересечения вспомогательной
плоскости с заданными; Определение линии пересечения плоскостей общего положения
3. Определить точку пересечения построенных линий;
8. Определить видимость .
Q
А
В
D
С
F
1
2
3
4
M
P
5
6
7
8
N
5. Найти линии пересечения вспомогательной плоскости с заданными;
6. Определить точку пересечения построенных линий;
4. Ввести вспомогательную проецирующую плоскость;
7. Найденные точки задают искомую линию пересечения;
Слайд 15
X
А2
В2
А1
В1
С2
С1
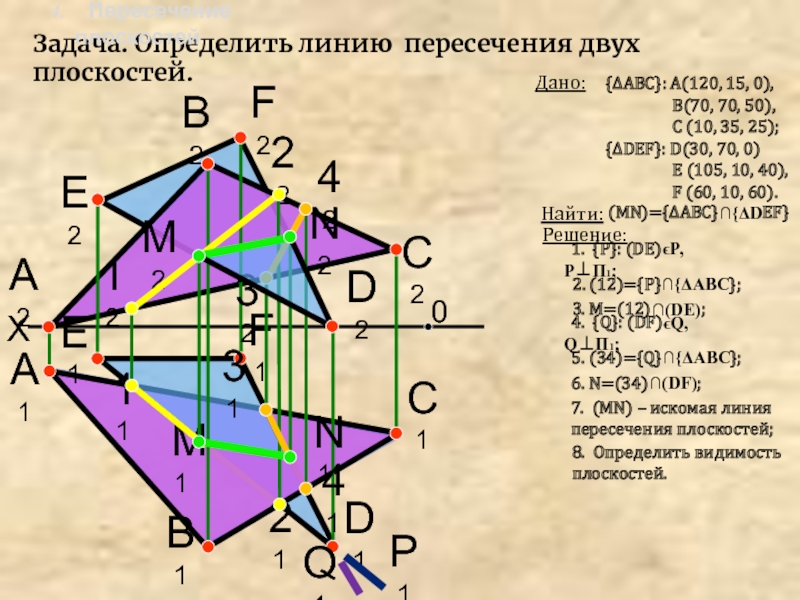
Задача. Определить линию пересечения двух плоскостей.
4. Пересечение
плоскостей
Дано:
{ΔАВС}: А(120, 15, 0),
В(70, 70, 50),С (10, 35, 25);
{ΔDEF}: D(30, 70, 0)
Е (105, 10, 40),
F (60, 10, 60).
1. {Р}: (DE)ϵP, P⊥П1;
D1
D2
M1
M2
Найти:
(MN)={ΔАВС}∩{ΔDEF}
Решение:
7. (MN) – искомая линия пересечения плоскостей;
E1
E2
F1
F2
N2
N1
0
Р1
2. (12)={Р}∩{ΔАВС};
22
21
12
11
3. М=(12)∩(DE);
4. {Q}: (DF)ϵQ, Q⊥П1;
Q1
42
41
32
31
5. (34)={Q}∩{ΔАВС};
6. N=(34)∩(DF);
8. Определить видимость плоскостей.
Слайд 16доценты кафедры «Начертательная геометрия, инженерная и компьютерная графика» Омского Государственного
технического университета:
Бондарев Олег Александрович, к.т.н.,
Кайгородцева Наталья Викторовна, к.пед.н.
Авторы:
