Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ, ДВУХ ПЛОСКОСТЕЙ
Содержание
- 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ, ДВУХ ПЛОСКОСТЕЙ
- 2. Прямая и точка в плоскостихА2В2С2С1А1В1l2l112221121D2D1Прямая принадлежит плоскости,
- 3. Главные линии плоскостихА2В2С2С1А1В1h2h112221121f2f1h ll П1; h
- 4. Прямая, параллельная плоскостиПрямая параллельна плоскости, если она
- 5. Параллельные плоскостиДве плоскости параллельны, если две пересекающиеся
- 6. Прямая, перпендикулярная плоскостиAanfhхh2h1f1f2A2A1n2n1Cогласно теореме о проецировании прямого
- 7. Построение взаимно перпендикулярных плоскостей основано на одном
- 8. Скачать презентанцию
Прямая и точка в плоскостихА2В2С2С1А1В1l2l112221121D2D1Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскостиТочка лежит в плоскости, если она лежит на прямой, расположенной в данной плоскости
Слайды и текст этой презентации
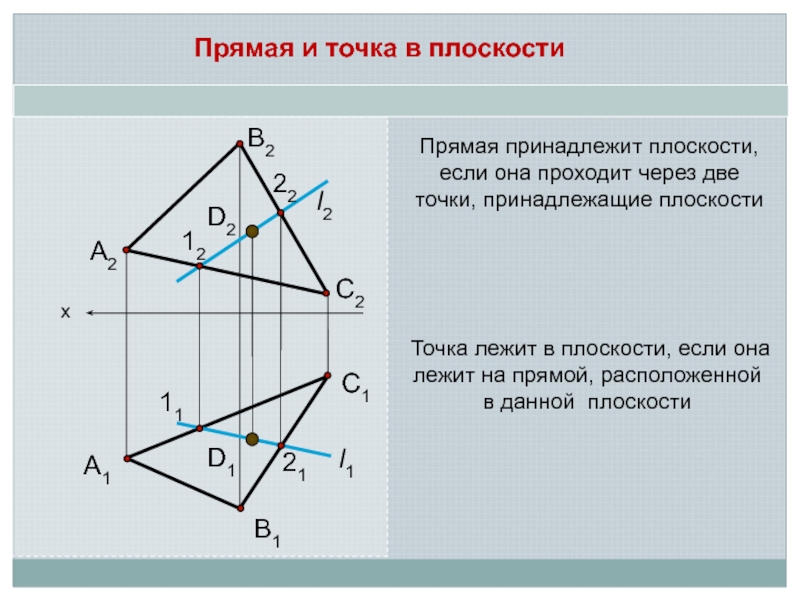
Слайд 2Прямая и точка в плоскости
х
А2
В2
С2
С1
А1
В1
l2
l1
12
22
11
21
D2
D1
Прямая принадлежит плоскости, если она проходит
через две точки, принадлежащие плоскости
лежит на прямой, расположенной в данной плоскости
Слайд 3Главные линии плоскости
х
А2
В2
С2
С1
А1
В1
h2
h1
12
22
11
21
f2
f1
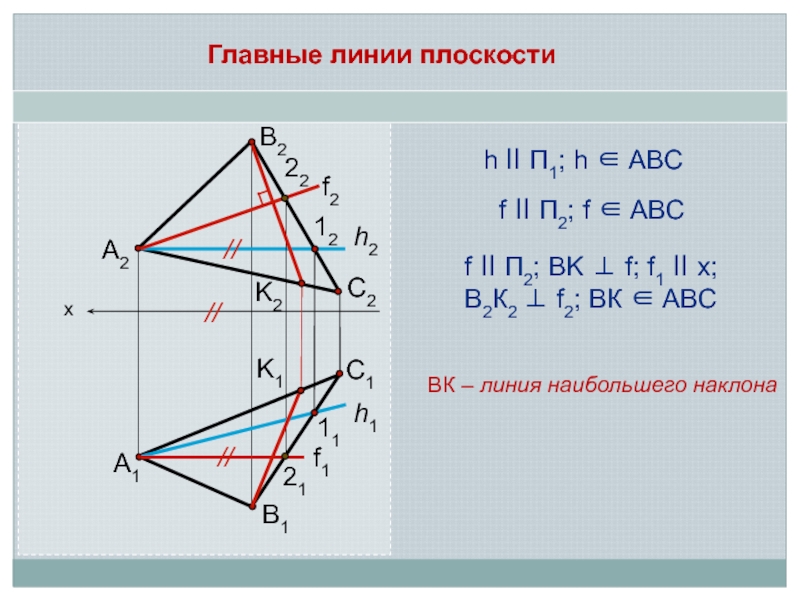
h ll П1; h ABC
K2
K1
f ll П2;
BK f; f1 ll x; В2К2 f2; ВК
ABCВК – линия наибольшего наклона
f ll П2; f ABC
//
//
//
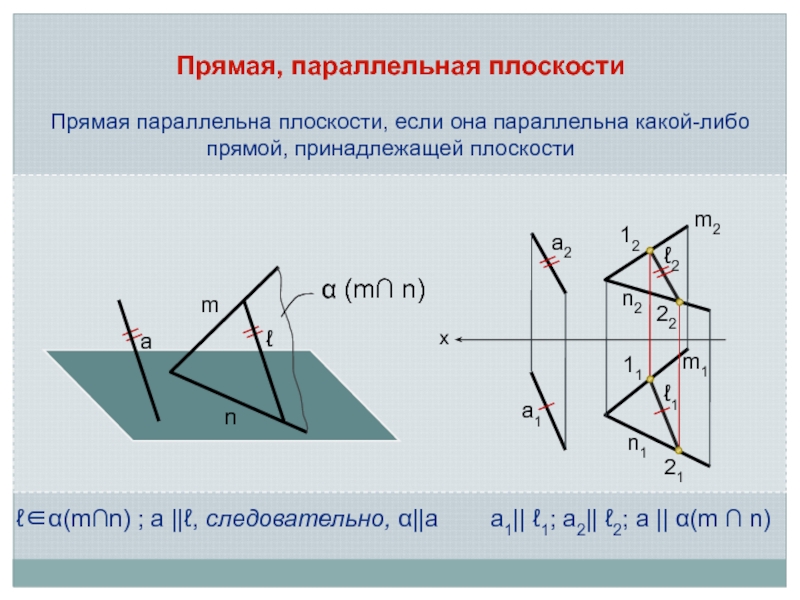
Слайд 4Прямая, параллельная плоскости
Прямая параллельна плоскости, если она параллельна какой-либо прямой,
принадлежащей плоскости
ℓ(m∩n) ; а
||ℓ, следовательно, ||аа1|| ℓ1; а2|| ℓ2; а || (m ∩ n)
х
a2
a1
m2
m1
n1
n2
ℓ2
ℓ1
//
//
/
/
12
11
22
21
a
m
n
ℓ
//
//
α (m∩ n)
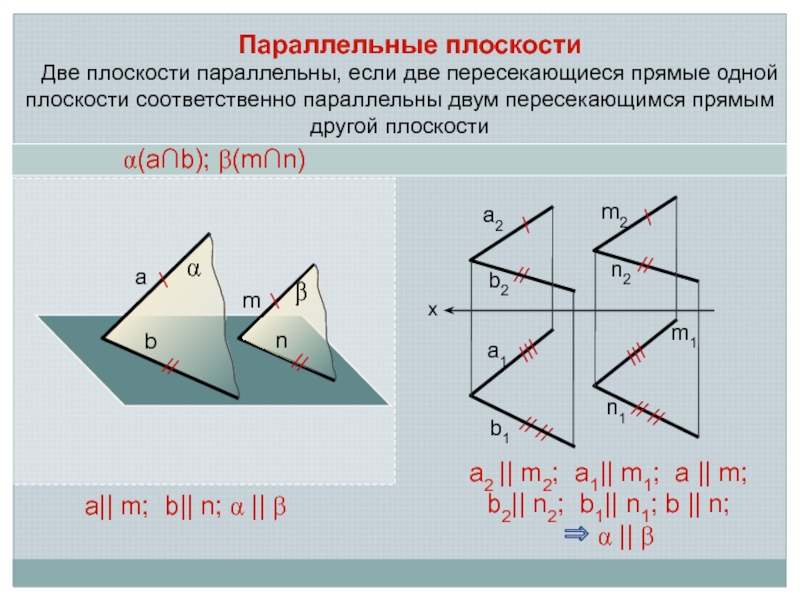
Слайд 5Параллельные плоскости
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости
соответственно параллельны двум пересекающимся прямым другой плоскости
а2 || m2; a1||
m1; a || m; b2|| n2; b1|| n1; b || n;
a || b
х
a2
a1
m2
m1
n1
n2
//
/
// //
a
//
b
a
//
/
/
b1
b2
///
//
/
// //
///
a(а∩b); b(m∩n)
а|| m; b|| n; a || b
b
n
m
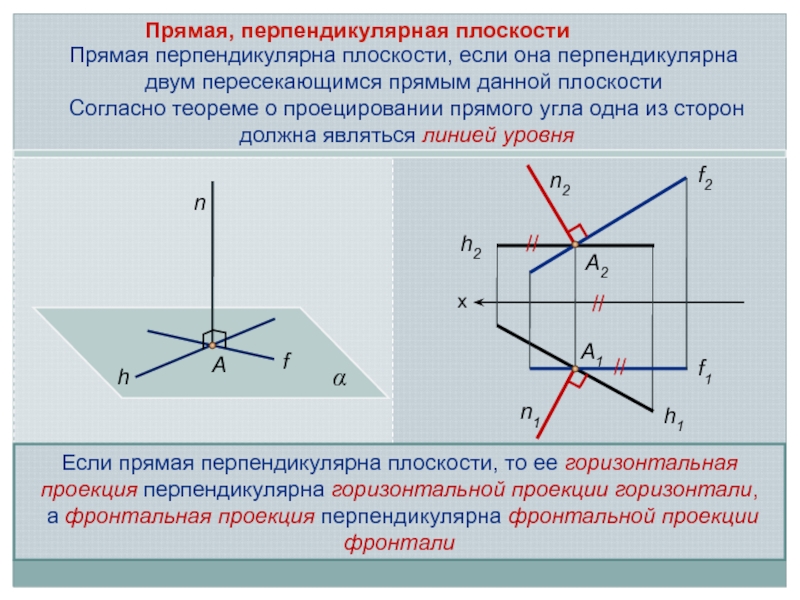
Слайд 6Прямая, перпендикулярная плоскости
A
a
n
f
h
х
h2
h1
f1
f2
A2
A1
n2
n1
Cогласно теореме о проецировании прямого угла одна из
сторон должна являться линией уровня
Если прямая перпендикулярна плоскости, то ее
горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали,а фронтальная проекция перпендикулярна фронтальной проекции фронтали
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым данной плоскости
//
//
//
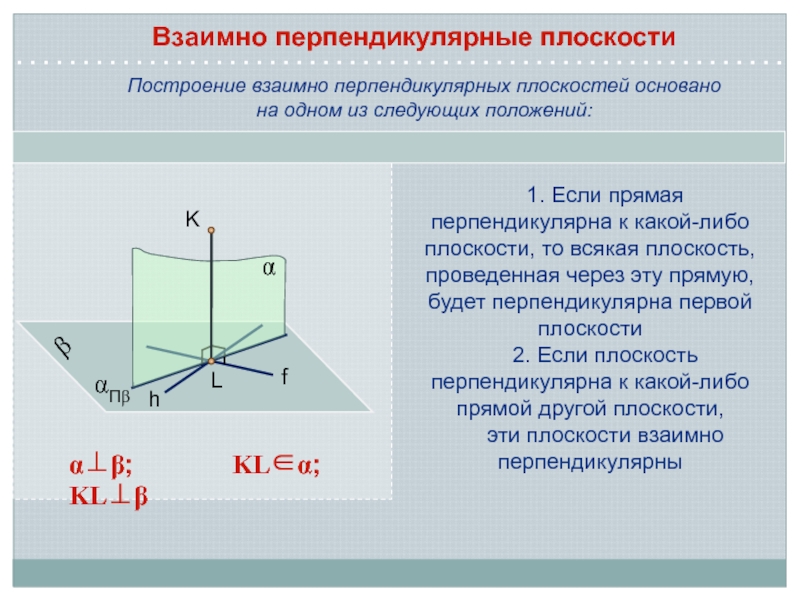
Слайд 7Построение взаимно перпендикулярных плоскостей основано
на одном из следующих положений:
1.
Если прямая перпендикулярна к какой-либо плоскости, то всякая плоскость, проведенная
через эту прямую, будет перпендикулярна первой плоскости2. Если плоскость перпендикулярна к какой-либо прямой другой плоскости,
эти плоскости взаимно перпендикулярны
L
K
f
h
a
b
aПb
Взаимно перпендикулярные плоскости
b; KL; KL
