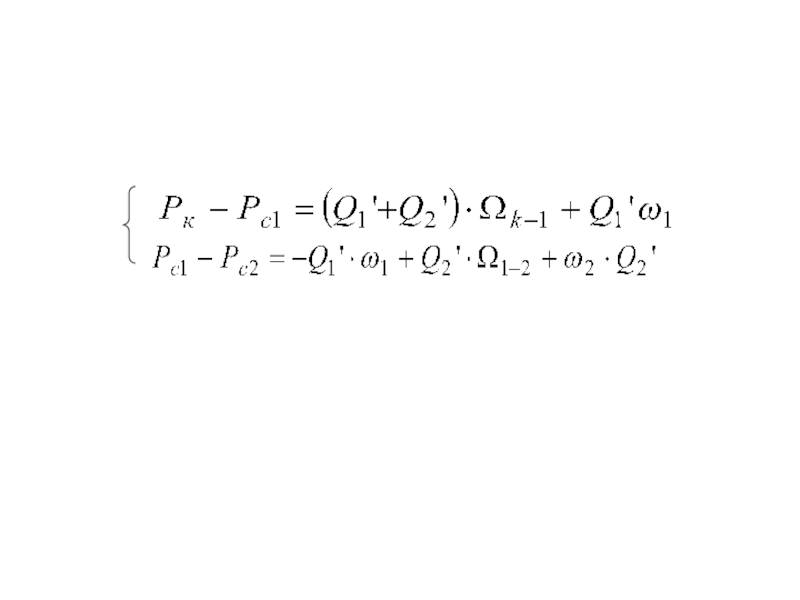Слайд 2Задача плоской интерференции (наложения) скважин.
Пласт - неограниченный, горизонтальный, имеет
постоянную мощность и непроницаемые подошву и кровлю.
Пласт вскрыт множеством
совершенных скважин и заполнен однородной жидкостью или газом.
Движение жидкости - установившееся, подчиняется закону Дарси и является плоским.
Плоское движение - течение происходит в плоскостях, параллельных между собой и картина движения во всех плоскостях идентична.
В связи с этим разбирается течение в одной из этих плоскостей - в основной плоскости течения.
Слайд 3Потенциал скорости фильтрации
потенциалом скорости фильтрации называется функция, производная которой с
обратным знаком вдоль линии тока равна скорости фильтрации.
В теории фильтрации
вводится функция Ф(x,y,z), называемая потенциалом скорости фильтрации (для горизонтального пласта)
Слайд 4Точечным источником называют точку на плоскости, поглощающую жидкость (модель нагнетательной
скважины бесконечно малого радиуса).
Точечным стоком называют точку на плоскости, отдающую
жидкость (модель добывающей скважины бесконечно малого радиуса).
На плоскости вокруг стока (источника) будет плоскорадиальное движение. Тогда скорость фильтрации запишется в виде
потенциала для точечного стока на плоскости (источник -)
Слайд 5ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
р=z R T – общий случай;
μ =const;
Слайд 7Формула Гиринского
Формула Маскета
Слайд 8Течение несжимаемой жидкости через недеформируемый (пористый) пласт
/плоско-радиальное течение/
Слайд 9Метод СУПЕРПОЗИЦИИ
При совместном действии в пласте нескольких стоков (эксплуатационных скважин)
или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником),
вычисляется по формуле для единственного стока (источника).
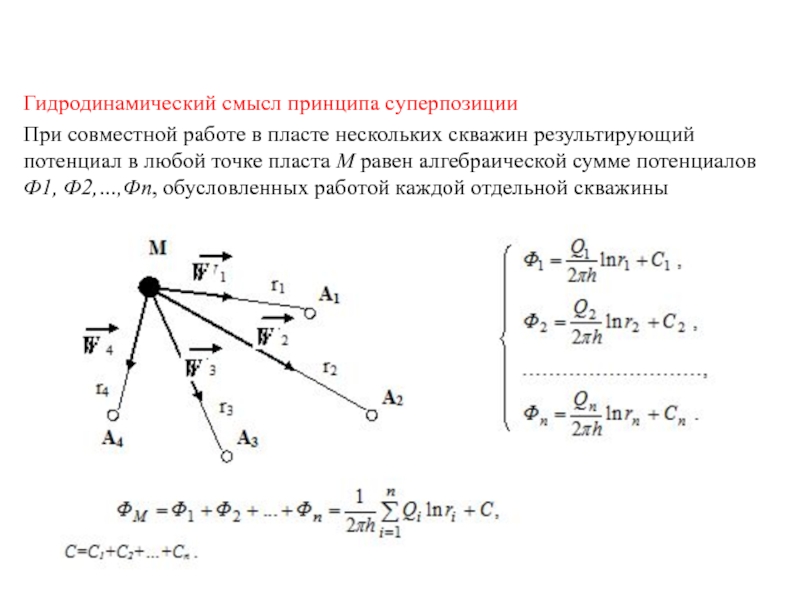
Слайд 10Гидродинамический смысл принципа суперпозиции
При совместной работе в пласте нескольких
скважин результирующий потенциал в любой точке пласта М равен алгебраической
сумме потенциалов Ф1, Ф2,…,Фn, обусловленных работой каждой отдельной скважины
Слайд 11
Скорости фильтрации при этом складываются геометрически.
фильтрационные потоки от работы каждого
источника или стока накладываются друг на друга
Используя принцип суперпозиции,
можно приближенно рассчитывать дебиты или потенциалы (а значит, забойные давления) для небольших групп скважин.
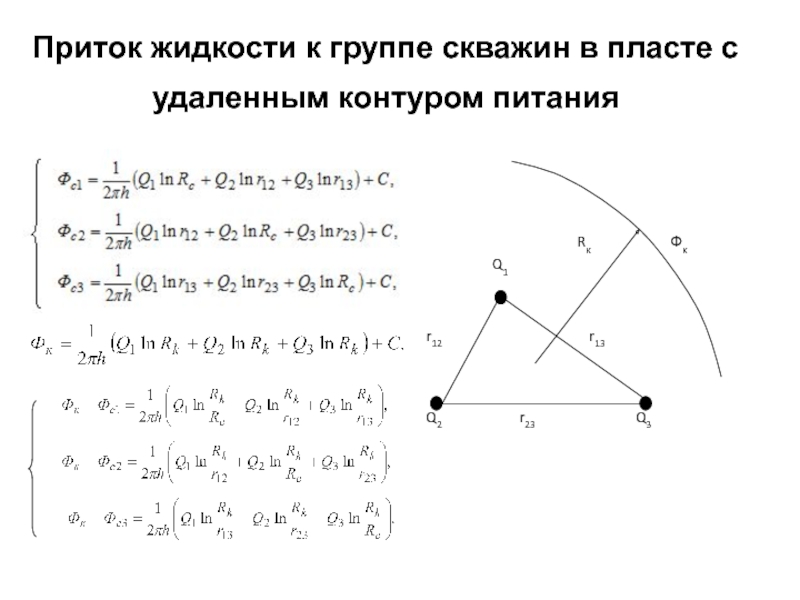
Слайд 12Приток жидкости к группе скважин в пласте с удаленным контуром
питания
Слайд 13Принцип суперпозиции можно использовать не только в бесконечных пластах, но
и в пластах, имеющих приближенный контур питания той или иной
формы, либо непроницаемую границу.
В этом случае вводятся фиктивные скважины-стоки или скважины-источники за пределами пласта и рассматривается их совместная работа с реальными скважинами.
Это – метод отображения источников-стоков.
Слайд 14Приток жидкости к скважине в пласте с прямолинейным контуром питания
Потенциал
в любой точке пласта М равен:
Потенциал на контуре питания
Фк
= С, поскольку для точки, помещенной на контур питания, r1=r2.
Потенциал на забое скважины А равен:
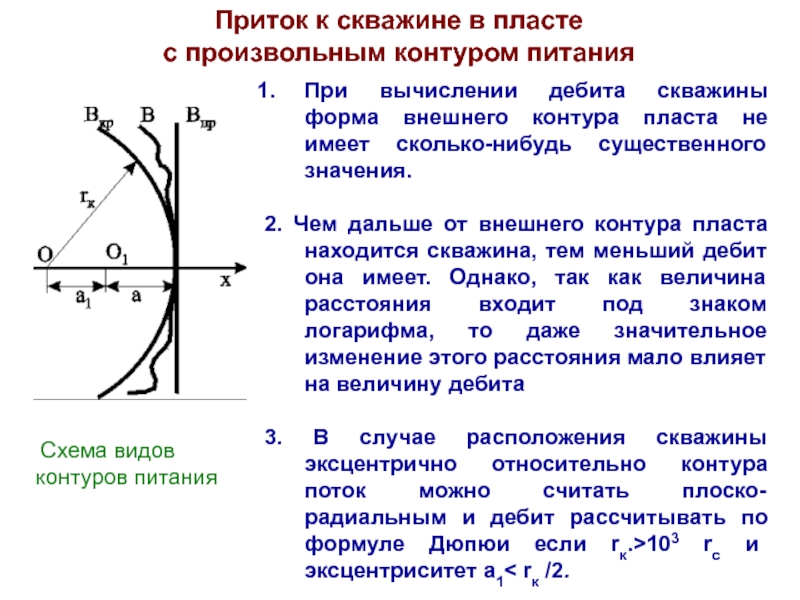
Слайд 15Приток к скважине в пласте
с произвольным контуром питания
Схема
видов
контуров питания
При вычислении дебита скважины форма внешнего контура пласта не
имеет сколько-нибудь существенного значения.
2. Чем дальше от внешнего контура пласта находится скважина, тем меньший дебит она имеет. Однако, так как величина расстояния входит под знаком логарифма, то даже значительное изменение этого расстояния мало влияет на величину дебита
3. В случае расположения скважины эксцентрично относительно контура поток можно считать плоско-радиальным и дебит рассчитывать по формуле Дюпюи если rк.>103 rc и эксцентриситет а1< rк /2.
Слайд 16ЭГДА (электрогидродинамическая аналогия)
1) изменение напряжения между узлами электрической сетки аналогично
распределению давления в пласте
2) электрическое сопротивление участка электрической сетки пропорционально
(аналогично) гидродинамическому сопротивлению участка моделируемого пласта
3) сила тока, протекающего между узлами сетки, пропорциональна (аналогична) количеству жидкости, протекающей через участок моделируемого пласта
Слайд 17При этом справедлив закон Кирхгофа, согласно которому суммарное падение напряжения
в сети равно сумме падений напряжений на отдельных участках:
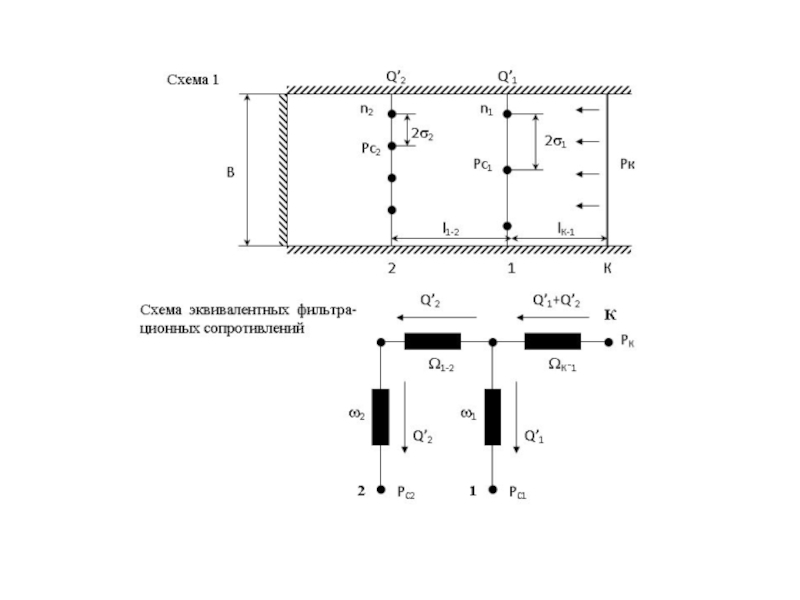
Слайд 18Приток к прямолинейной батарее скважин
Режим: удаленный контур питания и постоянные
забойные давления
Состав по числу скважин : четный и нечетный
Величина дебитов
скважин:равноудаленные от середины или от концов батареи - одинаковы, а при разной удаленности - отличаются.
Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости.
Эффекты взаимодействия
Слайд 19Метод эквивалентных фильтрационных сопротивлений предложен Ю.П.Борисовым и основан на аналогии
движения жидкости в пористой среде с течением электрического тока в
проводниках.
Для нахождения дебитов скважин цепочка скважин-стоков отображается зеркально относительно контура питания в скважины-источники, и рассматривается интерференция двух цепочек скважин в неограниченном пласте.
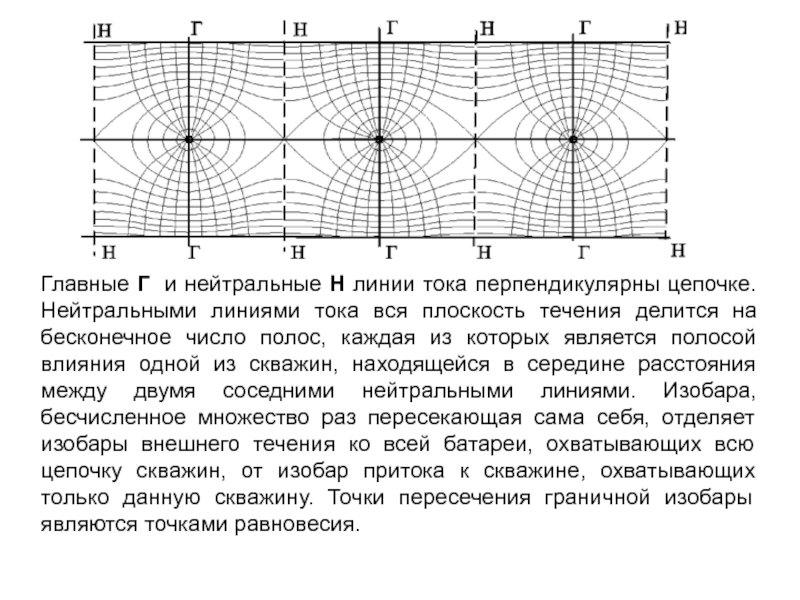
Слайд 20Главные Г и нейтральные Н линии тока перпендикулярны цепочке. Нейтральными
линиями тока вся плоскость течения делится на бесконечное число полос,
каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия.
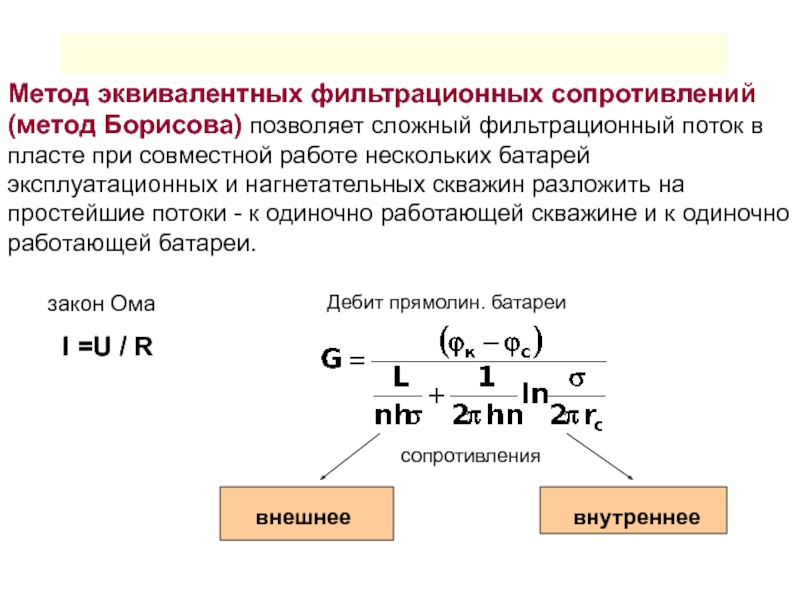
Слайд 22Метод эквивалентных фильтрационных сопротивлений (метод Борисова) позволяет сложный фильтрационный поток
в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных
скважин разложить на простейшие потоки - к одиночно работающей скважине и к одиночно работающей батареи.
закон Ома
I =U / R
Дебит прямолин. батареи
сопротивления
внешнее
внутреннее
Слайд 23Внешнее фильтрационное сопротивление - выражает фильтрационное сопротивление потоку от контура
питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в
предположении замены батареи галереей.
Дебит равен дебиту в прямолинейно-параллельном потоке через площадь величиной n h на длине L .
Внутреннее сопротивление - выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам за счет искривлений линий тока
Дебит равен суммарному дебиту n скважин при плоскорадиальном течении, в предположении, что каждая скважина окружена контуром питания длиной (аналог формулы Дюпюи)
Слайд 26внешние фильтрационные сопротивления
Внутренние фильтрационные сопротивления
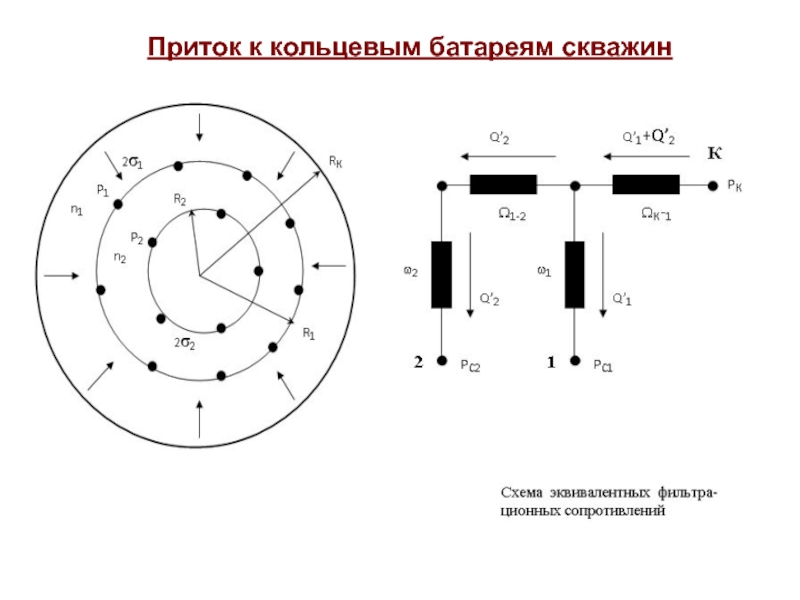
Слайд 27Приток к кольцевым батареям скважин
Слайд 28Внешние фильтрационные сопротивления
Внутренние фильтрационные сопротивления
Слайд 29Нейтральные линии тока Н - сходятся в центре батареи и
делят расстояние между двумя соседними скважинами пополам. Главные линии тока
Г - проходят через центры скважин и делят сектор, ограниченный двумя нейтральными линиями, пополам.
Слайд 30Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям
- минимальна. В центре кольцевой батареи скорость фильтрации равна нулю,
т.е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”.
Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой пересекающей себя в центре батареи столько раз, сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство - определяет приток к батарее в целом и представляет собой замкнутые кривые, описанные вокруг батареи.
Слайд 31Оценки эффекта взаимодействия скважин круговой батареи:
дебит изменяется непропорционально числу скважин
и радиусу батареи (расстоянию между скважинами);
с увеличением числа скважин
дебит каждой скважины уменьшается при постоянном забойном давлении, т.е. растет эффект взаимодействия;
взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт);
с увеличением числа скважин темп роста суммарного дебита батареи замедляется т.е. сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита.
Слайд 32Анализ
1) с увеличением числа эксплуатационных скважин кольцевой батареи влияние их
радиуса на дебит уменьшается, если отсутствует нагнетание жидкости в пласт;
2)
если в центре батареи находится нагнетательная скважина, то влияние радиуса скважины на дебит будет больше, чем при отсутствии центрального нагнетания жидкости в пласт.
3) радиус скважины влияет на производительность больше, чем при одиночной эксплуатационной скважине. Число скважин мало влияет на производительность.
Слайд 33Анизотропный пласт
Эффект взаимодействия будет значительно усиленным или ослабленным лишь
при резком различии проницаемостей в двух определённых направлениях: в направлении
линии расстановки скважин и в направлении перпендикулярном к этой линии.
Ослабление взаимодействия наблюдается в случае более низкой проницаемости в направлении линии расстановки скважин по сравнению с проницаемостью в перпендикулярном направлении. Усиление эффекта взаимодействия происходит в обратном случае. Таким образом, для уменьшения эффекта взаимодействия при закладывании новых скважин следует выбирать направление, в котором пласт наименее проницаем.