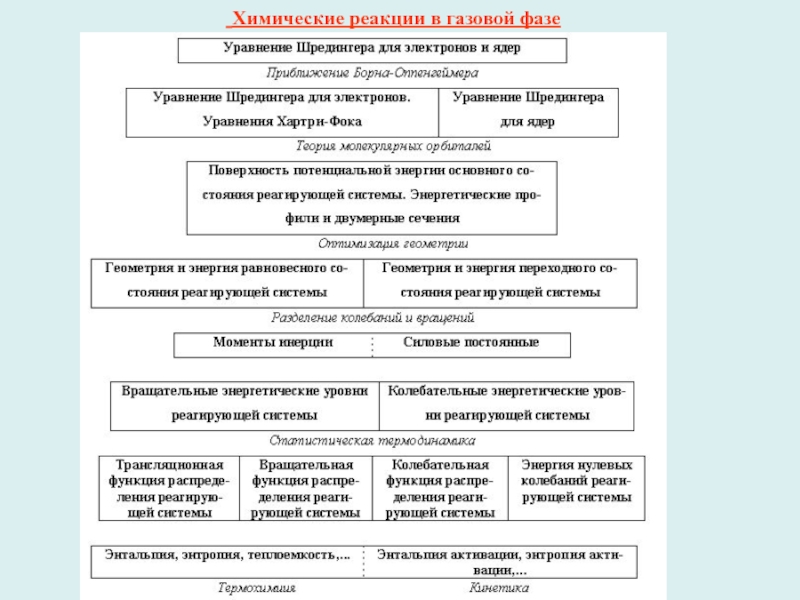
Слайд 1 Химические реакции в газовой фазе
Слайд 2Реакции между идеальными газами
1-й шаг - приближение Борна-Оппенгеймера. Затем
рассчитывают:
1. Поверхность потенциальной энергии (ППЭ) химической реакции (размерность ППЭ 3N–5)
- совокупность точек, определяющих полную энергию системы при различных фиксированных координатах ядер;
2. Путь химической реакции - линию минимальной энергии, непрерывно соединяющую долину исходных веществ и долину продуктов через точку локального максимума – переходное состояние;
3. Координату реакции - единственную координату, задающую путь химической реакции;
4. 5 особых точек сечения ППЭ вдоль координаты реакции:
1) Бесконечно удаленные реагенты;
2) Предреакционный комплекс;
3) Переходное состояние;
4) Послереакционный комплекс;
5) Бесконечно удаленные продукты.
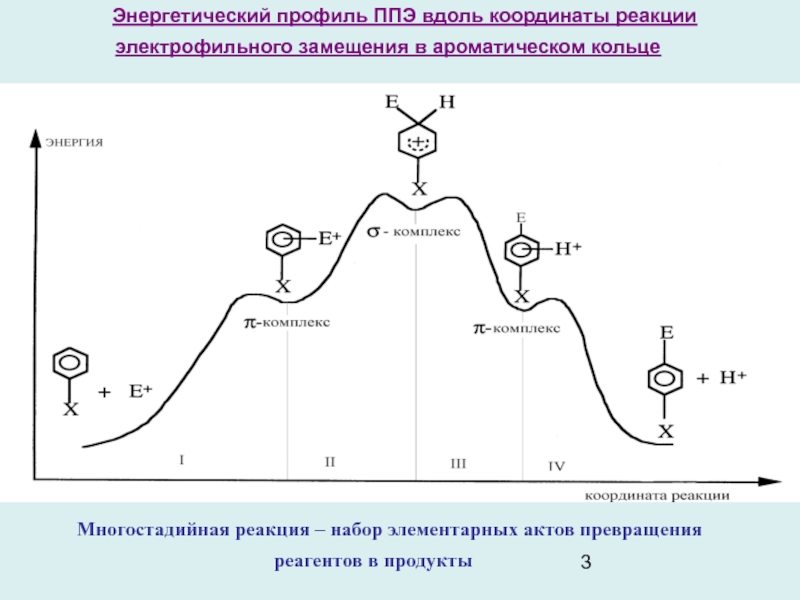
Слайд 3Энергетический профиль ППЭ вдоль координаты реакции электрофильного замещения в ароматическом
кольце
Многостадийная реакция – набор элементарных актов превращения реагентов в продукты
Слайд 4Энергетический профиль ППЭ вдоль координаты реакции для элементарного акта химической
реакции
Послереакционный
комплекс
Предреакционный
комплекс
Бесконечно удаленные реагенты
Бесконечно удаленные продукты реакции
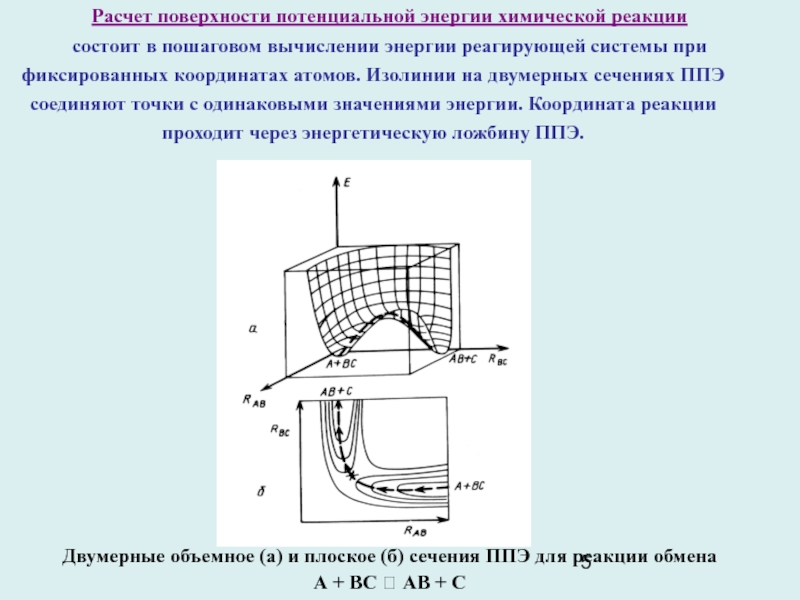
Слайд 5Расчет поверхности потенциальной энергии химической реакции
состоит в пошаговом вычислении
энергии реагирующей системы при фиксированных координатах атомов. Изолинии на двумерных
сечениях ППЭ соединяют точки с одинаковыми значениями энергии. Координата реакции проходит через энергетическую ложбину ППЭ.
Двумерные объемное (а) и плоское (б) сечения ППЭ для реакции обмена
А + BС ? AB + C
Слайд 6Расчет поверхности потенциальной энергии химической реакции
Особые точки ППЭ. Реагентам,
продуктам, пред- и послереакционным комплексам соответствуют локальные минимумы, а переходному
состоянию – седловая точка ППЭ, в которых выполняются условия стационарности
(U- потенциальная энергия):
∂U/∂Qi = 0, i = 1, 2,…, 3N–6(5).
В минимуме все собственные значения матрицы вторых производных G (матрицы Гессе или гессиана) положительны:
Gii = ∂2U/∂Qi2 > 0, i = 1, 2,…, 3N–6(5).
Qi, – нормальные колебательные координаты, в базисе которых матрица Гессе диагональна (∂2U/∂Qi∂Qj = 0, i≠j). Одно и только одно из собственных чисел гессиана отрицательно:
∂2U/∂Qr2 < 0, для некоторой координаты Qr ,
∂2 U/∂Qi2 > 0, при i ≠ r
Единственная нормальная координата в сечении ППЭ Qr , вдоль которой переходное состояние есть максимум, называется координатой реакции. В сечениях ППЭ вдоль остальных координат переходное состояние – минимум. Таким образом, переходное состояние есть седловая точка на ППЭ.
Наиболее эффективные методы поиска стационарных точек ППЭ – градиентные методы, например, метод наискорейшего спуска.

Слайд 7Путь химической реакции как метод локализации переходного состояния
Трудности:
1. Неоднозначность
2. Неинвариантность относительно ортогонального преобразования координат.
Решение проблемы неоднозначности (Фукуи): путь
химической реакции есть единственная внутренняя масс-взвешенная координата реакции (ВКР) Qi - путь наискорейшего спуска и, одновременно, путь минимальной энергии из переходного состояния на ППЭ в долину реагентов или продуктов, удовлетворяющий классическим уравнениям механики.
[ i-ая компонента масс-взвешенной координаты Qi = Σi mi½аiαi, αi = x, y, z; аi – коэффициенты разложения ВКР по декартовым координатам].
Основные методы определения пути химической реакции
переходное состояние известно - метод локальной квадратичной аппроксимации.
переходное состояние неизвестно - метод координаты реакции. Простейший путь реакции – энергетический профиль.
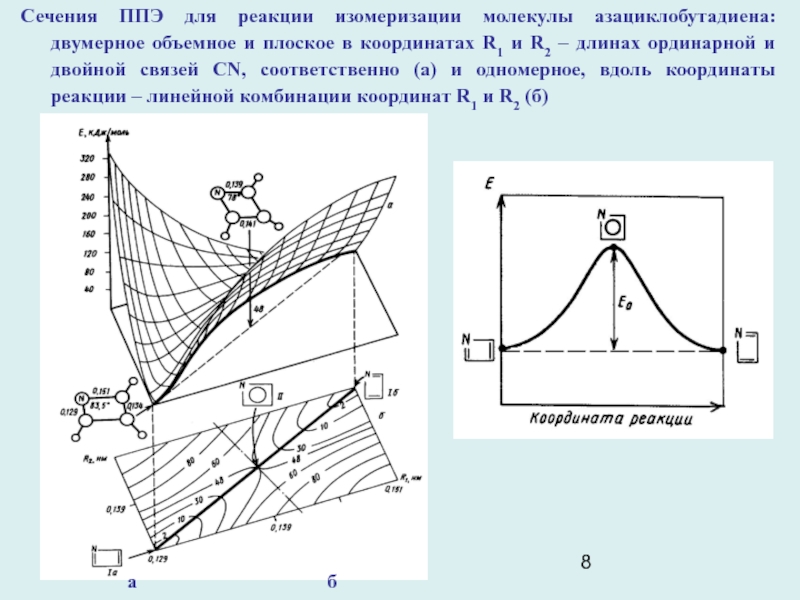
Слайд 8
Сечения ППЭ для реакции изомеризации молекулы азациклобутадиена: двумерное объемное и
плоское в координатах R1 и R2 – длинах ординарной и
двойной связей CN, соответственно (а) и одномерное, вдоль координаты реакции – линейной комбинации координат R1 и R2 (б)
а б
Слайд 9
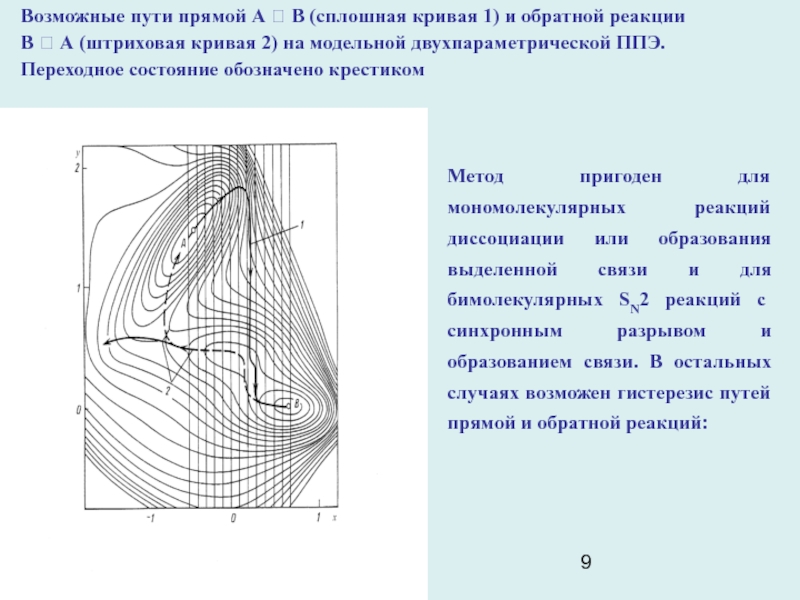
Возможные пути прямой А ? В (сплошная кривая 1) и
обратной реакции
В ? А (штриховая кривая 2) на модельной
двухпараметрической ППЭ.
Переходное состояние обозначено крестиком
Метод пригоден для мономолекулярных реакций диссоциации или образования выделенной связи и для бимолекулярных SN2 реакций с синхронным разрывом и образованием связи. В остальных случаях возможен гистерезис путей прямой и обратной реакций:
Слайд 10Матрицы Гессе равновесных и переходного состояний первой стадии реакции радикального
окисления метана (смотри выше), (МР2/UHF6-31G**) в базисе нормальных колебательных координат
Qi (см-1)
Реагенты СH4 :
H2: Gii =⏐ 4611 ⏐.
Переходное
состояние
[СH3---H−H]* :
Продукты СH3* :
Из сравннения колебательных частот - переходное состояние реагентоподобно.
Слайд 11Термодинамические характеристики и квантовая химия
Энтальпия реакции
H ≈ Eelec + E0vib
+ Evib(T) + Erot(T) + Etrans(T) + RT,
где Еelec
- электронная энергия.
Для реакций в газовой фазе используем формулы для идеальных газов:
(NkT – для линейных молекул, где N – постоянная Авогадро
Энергии колебаний являются функцией (3N-6) колебательных частот молекул:
Энергия нулевых колебаний :
Колебательный вклад в энтальпию (зависит от Т)
Слайд 12 Знак изменения свободной энергии Гиббса G определяет направление
химической реакции. G связана с энтальпией:
Энтропия определяется по формулам
, где
n-число молей молекул, М – масса молекулы.
Strans=
где и Iа - одна из главных компонент тензора момента инерции молекул
вырожденность электронного состояния
Слайд 14Роль орбитальной симметрии
Часто для описания реакции достаточно сведений о
ее стадиях, определяющих сближение реагентов и тип переходного состояния. Метод
МО играет здесь важную роль. Вудворд и Хоффман сформулировали принцип сохранения орбитальной симметрии, выполняющийся для реакций без промежуточных продуктов (согласованных реакций). Рассматриваются структура активных МО реагирующих веществ и знаки атомных орбиталей (АО), составляющих МО.
Правило Вудворда-Хоффмана гласит: реакция называется разрешенной по симметрии, если в ходе ее симметрия активных МО сохраняется.
К активным МО относятся все участвующие в реакции занятые и вакантные МО реагентов и продуктов. Деление реакций на разрешенные и запрещенные по симметрии осуществляется с помощью корреляционных диаграмм.
Пример: реакция диенового синтеза – циклоприсоединения цис-бутадиена к этилену с образованием циклогексен (реакции Дильса-Альдера). Эта реакция относится к числу перициклических, т.е. таких согласованных реакций, которые протекают с образованием циклических («замкнутых») переходных состояний, играющих определяющую роль.

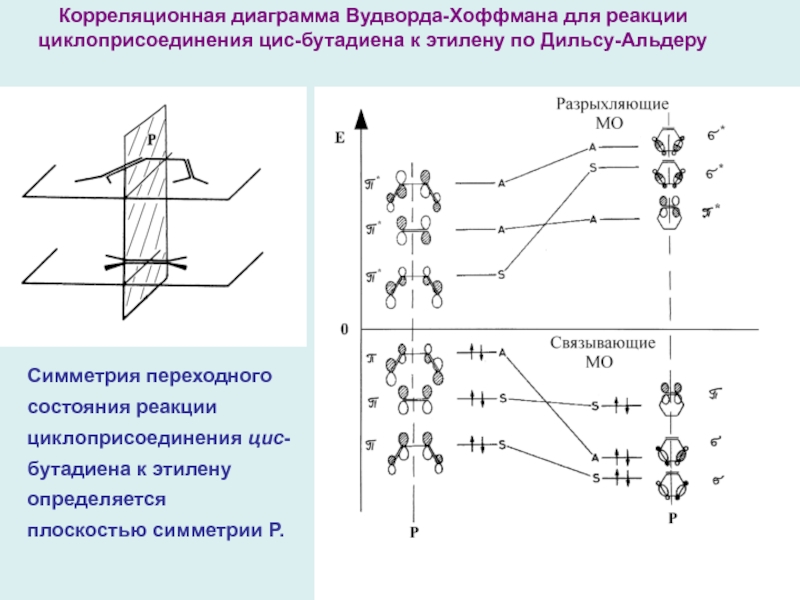
Слайд 15
Симметрия переходного состояния реакции циклоприсоединения цис-бутадиена к этилену определяется плоскостью
симметрии Р.
Корреляционная диаграмма Вудворда-Хоффмана для реакции циклоприсоединения цис-бутадиена к
этилену по Дильсу-Альдеру
Слайд 16 Классифицируем так же активные МО продукта реакции –
циклогексена: верхние занятые π, σ и нижние вакантные π*, σ*
МО вновь образованных двойной и двух ординарных СС связей.
Корреляционную диаграмму взаимодействия между реагентами и продуктом следует строить простым соединением МО с одинаковой симметрией ( S → S и A → A ), учитывая, что разность энергий МО должна быть минимальна. Если это возможно и ни одна из соединяющих линий не пересекает нулевого уровня (правило непересечения), то реакция «разрешена» по симметрии. Результат - корреляционная диаграмма Вудворда-Хоффмана для реакции Дильса-Альдера, на которой связывающие МО реагентов взаимодействуют только со связывающими МО продукта, а разрыхляющие МО реагентов – только с разрыхляющими МО продукта – реакция «разрешена» по симметрии .
Правило Вудворда-Хоффмана может быть приложено и к реакциям замещенных полиенов, когда симметрия отсутствует. В этом случае рассматриваются корреляции между МО незамещенных аналогов.
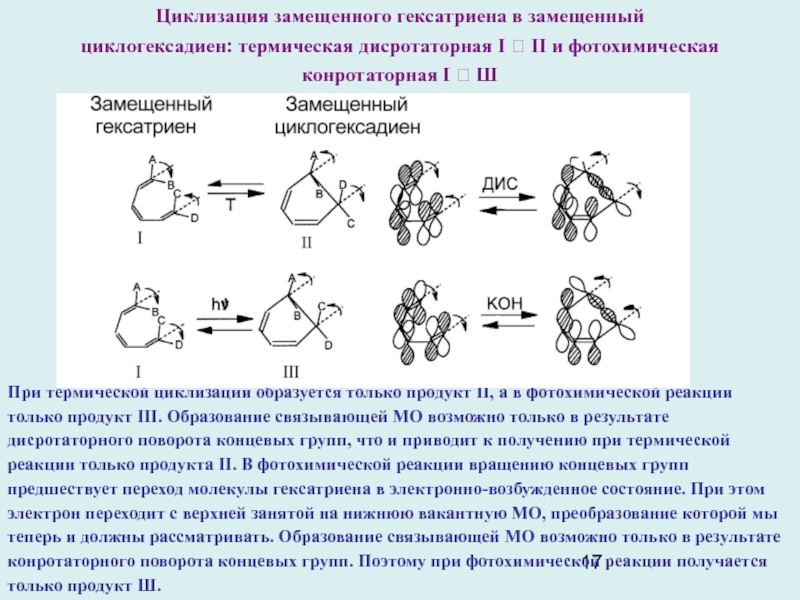
Слайд 17При термической циклизации образуется только продукт II, а в фотохимической
реакции только продукт III. Образование связывающей МО возможно только в
результате дисротаторного поворота концевых групп, что и приводит к получению при термической реакции только продукта II. В фотохимической реакции вращению концевых групп предшествует переход молекулы гексатриена в электронно-возбужденное состояние. При этом электрон переходит с верхней занятой на нижнюю вакантную МО, преобразование которой мы теперь и должны рассматривать. Образование связывающей МО возможно только в результате конротаторного поворота концевых групп. Поэтому при фотохимической реакции получается только продукт Ш.
Циклизация замещенного гексатриена в замещенный
циклогексадиен: термическая дисротаторная I ? II и фотохимическая
конротаторная I ? Ш
Слайд 18Индексы реакционной способности
Индексами реакционной способности (ИРС) называются
полученные в результате квантово-химических расчетов электронные и энергетические характеристики системы,
которые коррелируют с экспериментальными данными о реакционной способности.
ИРС делятся на две группы. Первые определяются в приближении реагирующей молекулы (приближении локализации), когда учитывают свойства переходного состояния химической реакции. Вторые – в приближении изолированной молекулы с учетом статических свойств лишь исходных веществ или предреакционного комплекса: структуры и энергии граничных МО, зарядов, порядков связей и т.д.
Валентность атома и порядок связи
Реакционную способность молекул характеризуют такими статическими ИРС, как валентность и заряд атомов, кратность связей. Соответствующие индексы валентности VA, заряда на атомах qA порядка связи по Коулсону РAB или по Вайбергу IAB определяются структурой МО μ и ν атомов А и В, точнее произведениями диагональных и недиагональных элементов матрицы зарядов и порядков связей Рμν и матрицы интегралов перекрывания Sμν :

μ∈Α, ν∈Β
IAB
=Σ⏐Pμν Sμν⏐2
μ∈A, ν∈B VA = ∑РAB
Β≠Α
Индексы связей сохраняют свои значения при отклонении длины связи от равновесной. Например, в молекулах этана, этилена и ацетилена при варьировании равновесной длины связи от ординарной до тройной они сохраняют близость к значениям, соответственно, 1.0, 2.0, 3.0.
Индексы Уайберга IСС, вычисленные при равновесным длинах связей RCC
Важной особенностью индексов VA, РAB, IAB является их инвариантность относительно унитарного преобразования базисных орбиталей.
Слайд 20 Молекулярный электростатический потенциал
молекулярный электростатический потенциал (МЭП) в
точке r пространства внутри и вне молекулы:
где Zα⎪e⎪ и Rα
– заряд и радиус-вектор ядра α, ρ(r) - электронная плотность.
Энергетическая карта молекулярного электростатического
потенциала формамида в плоскости молекулы.
(Энергия дана в кДж/моль. Отрицательный потенциал показан сплошными линиями)
Слайд 21
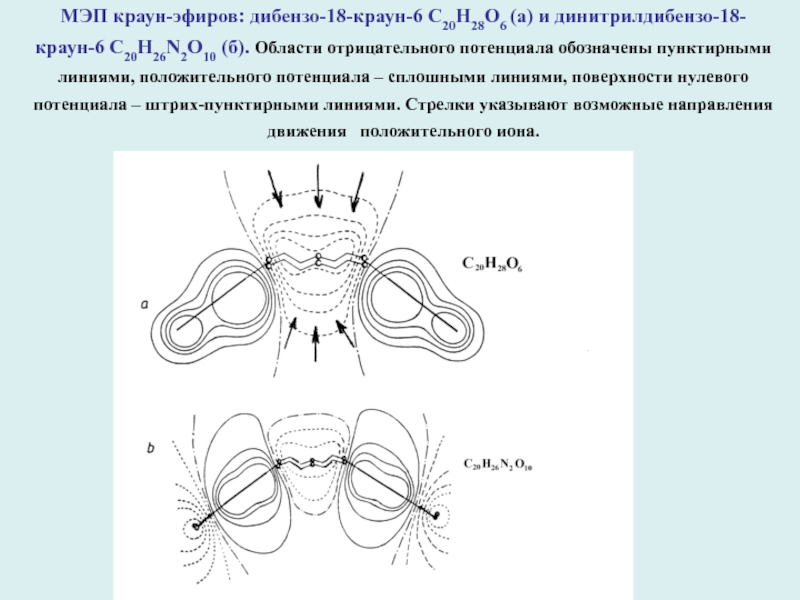
МЭП краун-эфиров: дибензо-18-краун-6 С20Н28О6 (а) и динитрилдибензо-18-краун-6 С20Н26N2О10 (б). Области
отрицательного потенциала обозначены пунктирными линиями, положительного потенциала – сплошными линиями,
поверхности нулевого потенциала – штрих-пунктирными линиями. Стрелки указывают возможные направления движения положительного иона.
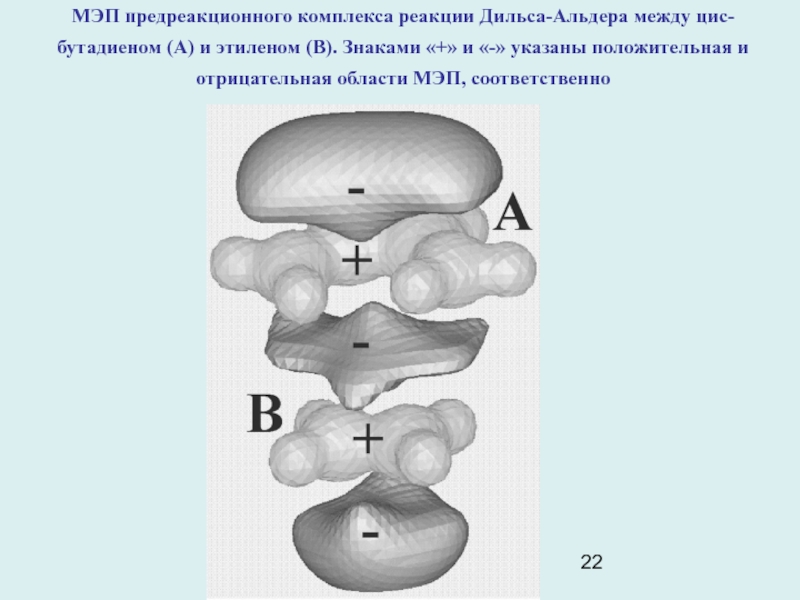
Слайд 22МЭП предреакционного комплекса реакции Дильса-Альдера между цис-бутадиеном (А) и этиленом
(В). Знаками «+» и «-» указаны положительная и отрицательная области
МЭП, соответственно
Слайд 23 Метод граничных орбиталей
Метод граничных орбиталей Фукуи, определяет
относительную реакционную способность соединений по энергии граничных МО: верхней занятой
(ВЗМО) нуклеофила или нижней вакантной (НВМО) электрофила. Положительная энергия НВМО определяет нуклеофильные свойства молекулы, отрицательная – электрофильные. Предпочтительные места атаки определяются индексом реакционной способности – электронным вкладом атома r в заселенность граничной МО:
где ciμ , ciν– коэффициенты разложения ВЗМО (НВМО) i по АО χμ ,χν атома r. Реакционный центр отождествляется с атомом, для которого fr максимально.
Слайд 24 Теория жестких и мягких кислот и оснований
Все
соединения делятся на два больших класса. Региоселективность взаимодействия в одном
из них определяются зарядами на атомах qr, во втором – граничной плотностью электрона на атоме fr.
Согласно Пирсону можно выделить «мягкие» и «жесткие» кислоты и основания (как Бренстеда, так и Льюиса). «Жесткие» кислоты (H+, Li+, Na+, K+, BF3, AlCl3 и т.д.) должны быстрее реагировать с «жесткими» основаниями (OH–, F–, Cl–, SO42–, NH3, RNH2 и т.д.), а «мягкие» кислоты – с «мягкими» основаниями.
Четыре возможных случая кислотно-основного взаимодействия (в скобках указан тип взаимодействия с точки зрения теории ЖМКО) :
а. Граничных МО;
б. МЭП кислоты (пунктирная линия) и основания (сплошная линия совпадает с ионным радиусом)
Слайд 25 Взаимодействие «мягкий-мягкий» предпочтительно из-за сильного взаимодействия ВЗМО нуклеофила
– НВМО электрофила с небольшой разностью энергий и значительной поляризуемостью.
Поляризуемость характеризует степень деформации электронной плотности молекулы в электростатическом поле, создаваемом партнером по реакции. Высокая поляризуемость обеспечивается значительной удаленностью электронной пары от атомного ядра, т.е большим ионным радиусом.
Взаимодействие «жесткий-жесткий» энергетически более выгодно, чем вариант «жесткий-мягкий» потому, что жесткие соединения порождают сильный МЭП. Кроме того, заряды на атомах жестких соединений больше, чем на атомах «мягких». Поэтому высокая энергия электростатического взаимодействия компенсирует небольшую стабилизацию предреакционного комплекса за счет взаимодействия граничных МО (Клопман).
Концепция Пирсона охватывает два различных типа реакций: «контролируемые граничными орбиталями» и «контролируемые зарядом».
- Реакция считается орбитально контролируемой, если основным вкладом в энергию межмол. взаимодействия предреакционного комплекса является Еинд = Епол + Едисп . В этом случае ВЗМО нуклеофила и НВМО электрофила отделены от других занятых и вакантных МО энергетической щелью не менее 1эВ.
- Реакция считается зарядово контролируемой, если основным вкладом в энергию ММВ предреакционного комплекса является Еэл.стат. При этом величина энергетической щели, отделяющей ВЗМО нуклеофила и НВМО электрофила от других занятых и вакантных МО гораздо меньше 1 эВ. Так, реакция Дильса-Альдера, по крайней мере на начальных стадиях, является зарядово контролируемой, чем и объясняется ее достаточно высокий энергетический барьер.
Поскольку МЭП отражает распределение полной плотности заряда, включающей ядра, а не электронной плотности МО, то он имеет предсказательную силу лишь в отношении реакций, контролируемых распределением зарядов на атомах. Граничная плотность электрона fr на атоме r, напротив, определяет оптимальные места атак лишь в орбитально контролируемых реакциях.

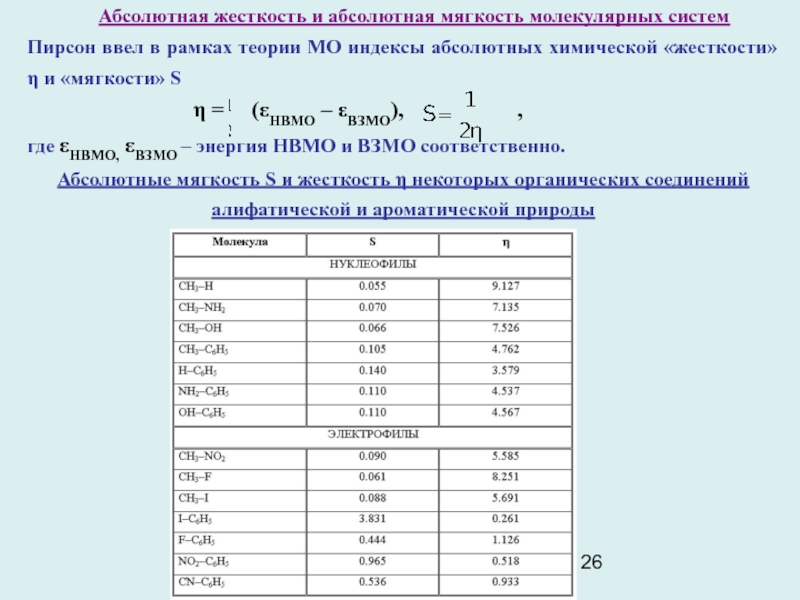
Слайд 26 Абсолютная жесткость и абсолютная мягкость молекулярных систем
Пирсон ввел
в рамках теории МО индексы абсолютных химической «жесткости» η и
«мягкости» S
η = (εНВМО – εВЗМО), ,
где εНВМО, εВЗМО – энергия НВМО и ВЗМО соответственно.
Абсолютные мягкость S и жесткость η некоторых органических соединений
алифатической и ароматической природы
Слайд 27 Функции Фукуи
Абсолютные жесткость η и мягкость S
связаны с локальной жесткостью h (r) и локальной мягкостью s(r)
через функцию Фукуи f(r):
s(r) = f(r) s(r), η(r) = f(r) h(r).
По Парру и Янгу функциями Фукуи называются функции, определяющие локальные изменения электронной плотности ρ(r) при увеличении f+(r) или уменьшении f – (r) числа электронов в системе :
f+(r) = ρN0+1(r) – ρN0(r), f -(r) = ρN0(r) – ρN0-1(r).
Карты функций Фукуи опредяют наиболее предпочтительные места электрофильной, нуклеофильной и радикальной атак.
Пример - молекула Н2СО. Наиболее предпочтительным центром нуклеофильной атаки является атом углерода, которому соответствует глобальный максимум функции Фукуи f+(r), а электрофильной и радикальной атак – атом кислорода, которому соответствуют глобальные максимумы функции Фукуи f – (r) и функции Фукуи f0(r) = (f+(r) + f – (r))/2, соответственно.
Слайд 28Контурная карта функции Фукуи для молекулы Н2СО (интервал между контурами
0.005 а.е.) : f+(r) в плоскости,перпендикулярной плоскости молекулы Н2СО (а)
; f – (r) в плоскости молекулы Н2СО (б) ; f0(r) в плоскости, перпендикулярной плоскости молекулы Н2СО (в). Координата атома углерода на оси абсцис 1.015 а.е., атома кислорода –1.27 а.е.
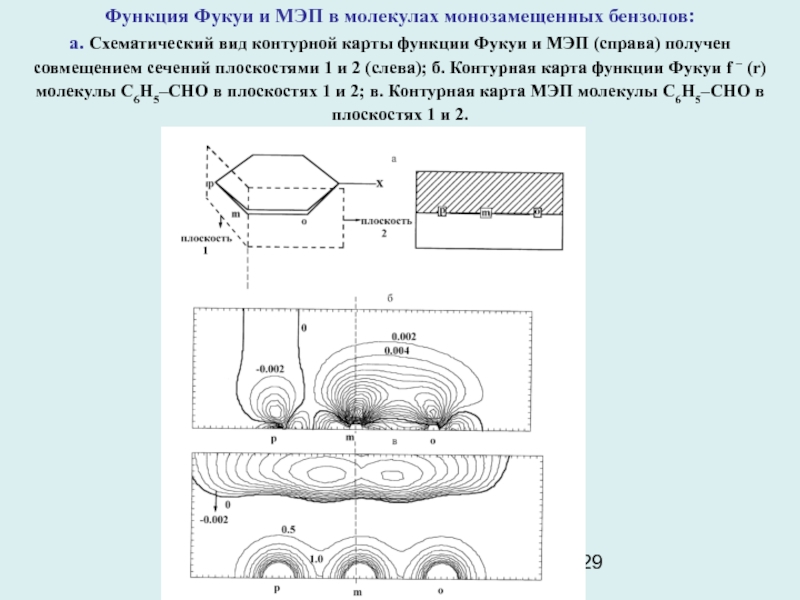
Слайд 29Функция Фукуи и МЭП в молекулах монозамещенных бензолов:
а. Схематический
вид контурной карты функции Фукуи и МЭП (справа) получен совмещением
сечений плоскостями 1 и 2 (слева); б. Контурная карта функции Фукуи f – (r) молекулы С6Н5–CHO в плоскостях 1 и 2; в. Контурная карта МЭП молекулы С6Н5–CHO в плоскостях 1 и 2.