TheSlide.ru

Задача поиска минимального остовного дерева

Содержание

1. Задача поиска минимального остовного дерева
2. Исходный неориентированный граф (слева) и его минимальный покрывающий остов (справа).Алгоритм Прима
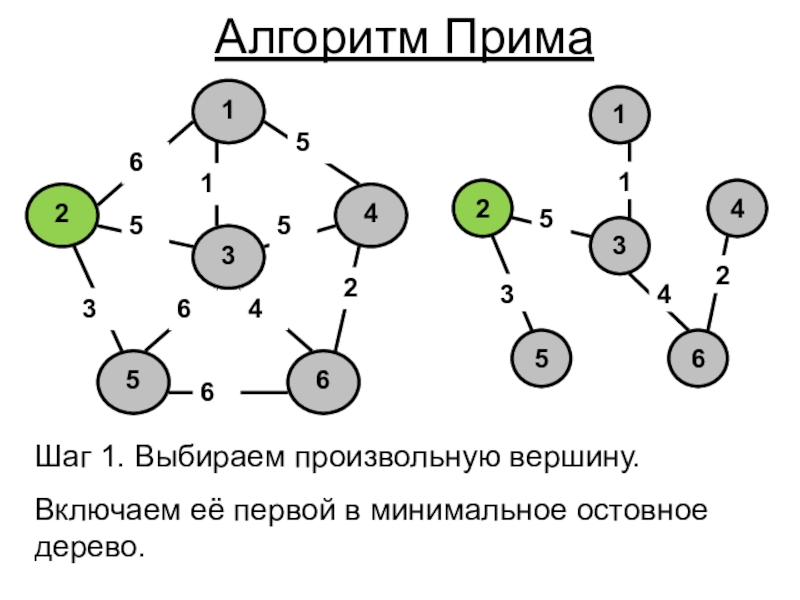
3. Шаг 1. Выбираем произвольную вершину.Включаем её первой в минимальное остовное дерево.Алгоритм Прима
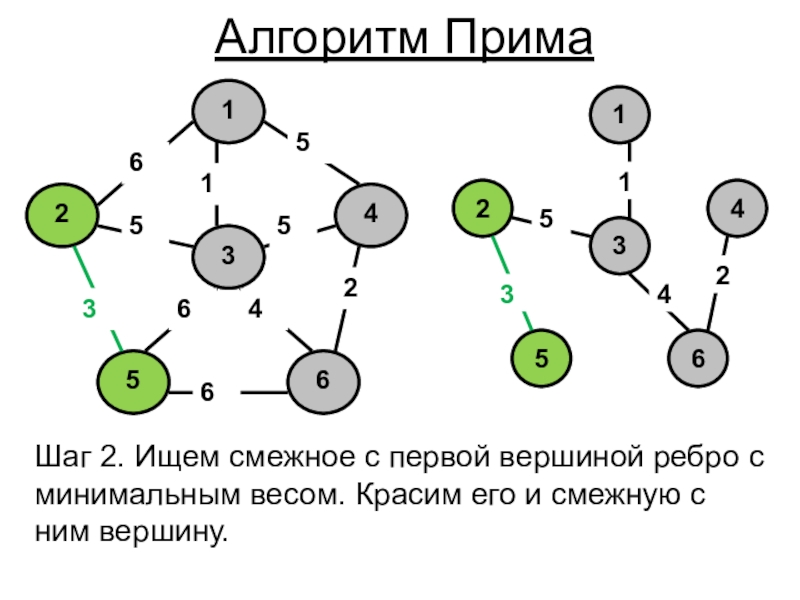
4. Шаг 2. Ищем смежное с первой вершиной
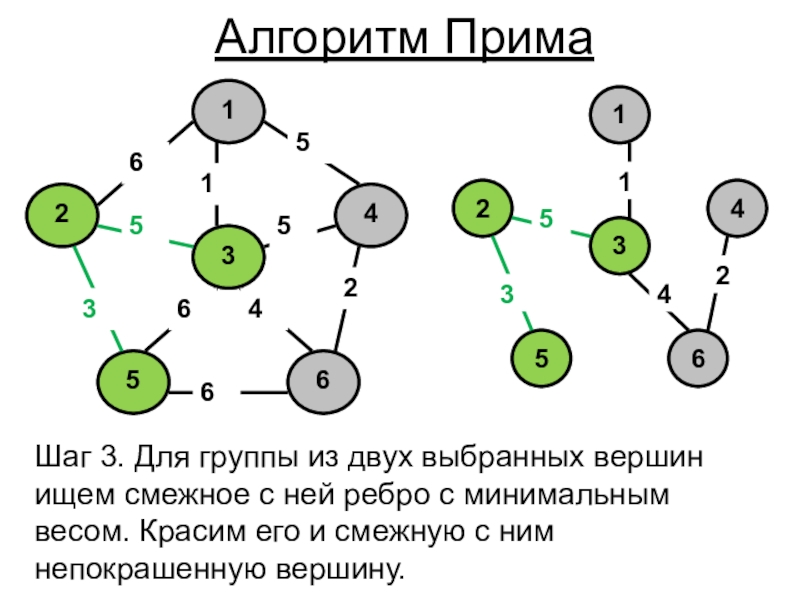
5. Шаг 3. Для группы из двух выбранных
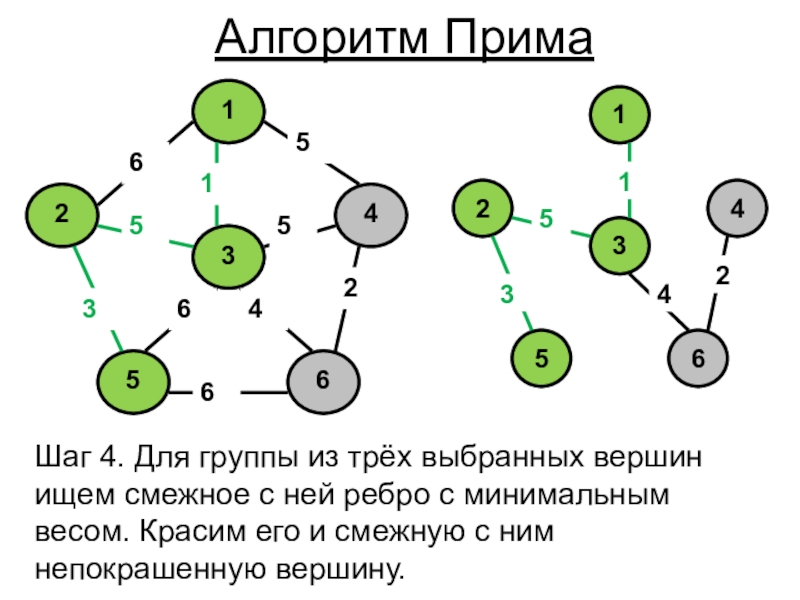
6. Шаг 4. Для группы из трёх выбранных
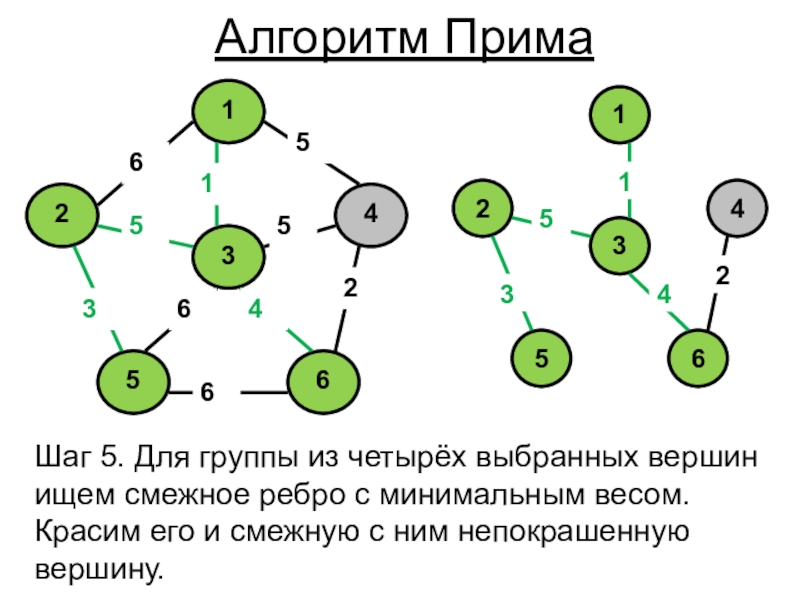
7. Шаг 5. Для группы из четырёх выбранных
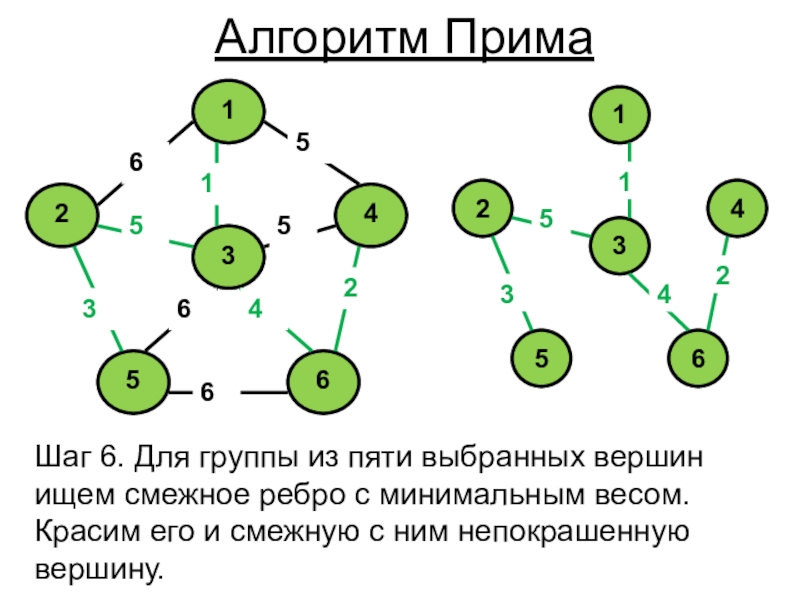
8. Шаг 6. Для группы из пяти выбранных
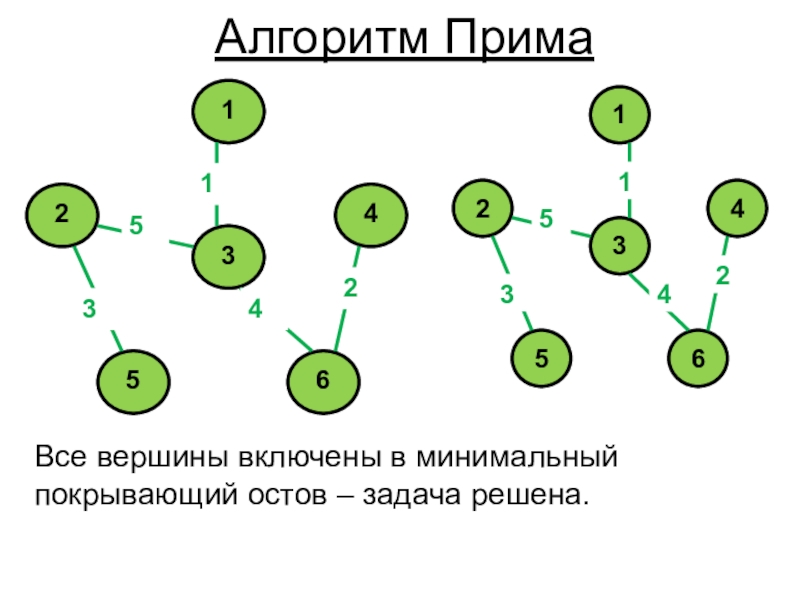
9. Все вершины включены в минимальный покрывающий остов – задача решена.Алгоритм Прима
10. Скачать презентанцию

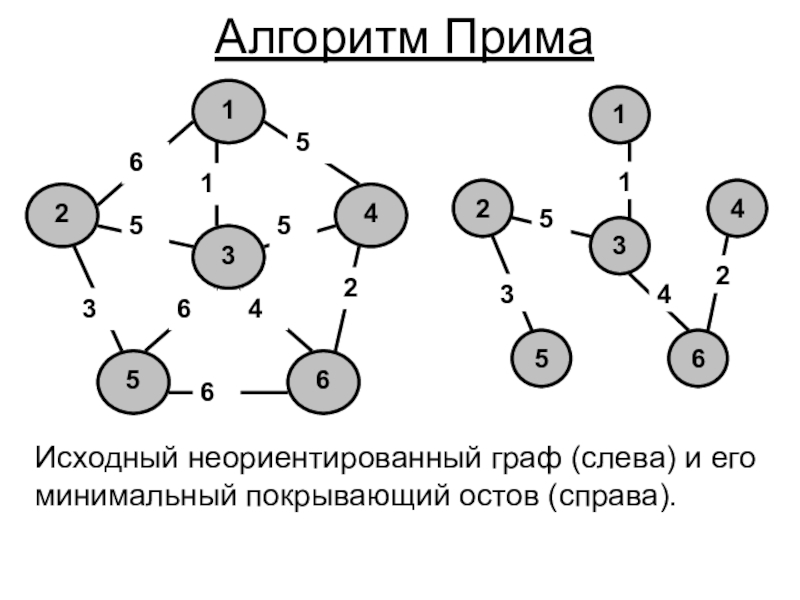
Исходный неориентированный граф (слева) и его минимальный покрывающий остов (справа).Алгоритм Прима

Главная
Разное
Задача поиска минимального остовного дерева

Слайды и текст этой презентации

Слайд 1Задача поиска минимального остовного дерева.
Задача. Построить минимальное остовное дерево (кратчайшую

связывающую сеть) – соединение всех узлов сети с помощью путей

наименьшей длины.

Задача поиска минимального остовного дерева.Задача. Построить минимальное остовное дерево (кратчайшую связывающую сеть) – соединение всех узлов сети

Слайд 2Исходный неориентированный граф (слева) и его минимальный покрывающий остов (справа).
Алгоритм

Прима

Исходный неориентированный граф (слева) и его минимальный покрывающий остов (справа).Алгоритм Прима

Слайд 3Шаг 1. Выбираем произвольную вершину.
Включаем её первой в минимальное остовное

дерево.
Алгоритм Прима

Шаг 1. Выбираем произвольную вершину.Включаем её первой в минимальное остовное дерево.Алгоритм Прима

Слайд 4Шаг 2. Ищем смежное с первой вершиной ребро с минимальным

весом. Красим его и смежную с ним вершину.
Алгоритм Прима

Шаг 2. Ищем смежное с первой вершиной ребро с минимальным весом. Красим его и смежную с ним

Слайд 5Шаг 3. Для группы из двух выбранных вершин ищем смежное

с ней ребро с минимальным весом. Красим его и смежную

с ним непокрашенную вершину.

Алгоритм Прима

Шаг 3. Для группы из двух выбранных вершин ищем смежное с ней ребро с минимальным весом. Красим

Слайд 6Шаг 4. Для группы из трёх выбранных вершин ищем смежное

с ней ребро с минимальным весом. Красим его и смежную

с ним непокрашенную вершину.

Алгоритм Прима

Шаг 4. Для группы из трёх выбранных вершин ищем смежное с ней ребро с минимальным весом. Красим

Слайд 7Шаг 5. Для группы из четырёх выбранных вершин ищем смежное

ребро с минимальным весом. Красим его и смежную с ним

непокрашенную вершину.

Алгоритм Прима

Шаг 5. Для группы из четырёх выбранных вершин ищем смежное ребро с минимальным весом. Красим его и

Слайд 8Шаг 6. Для группы из пяти выбранных вершин ищем смежное

ребро с минимальным весом. Красим его и смежную с ним

непокрашенную вершину.

Алгоритм Прима

Шаг 6. Для группы из пяти выбранных вершин ищем смежное ребро с минимальным весом. Красим его и

Слайд 9Все вершины включены в минимальный покрывающий остов – задача решена.
Алгоритм

Прима

Все вершины включены в минимальный покрывающий остов – задача решена.Алгоритм Прима

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей