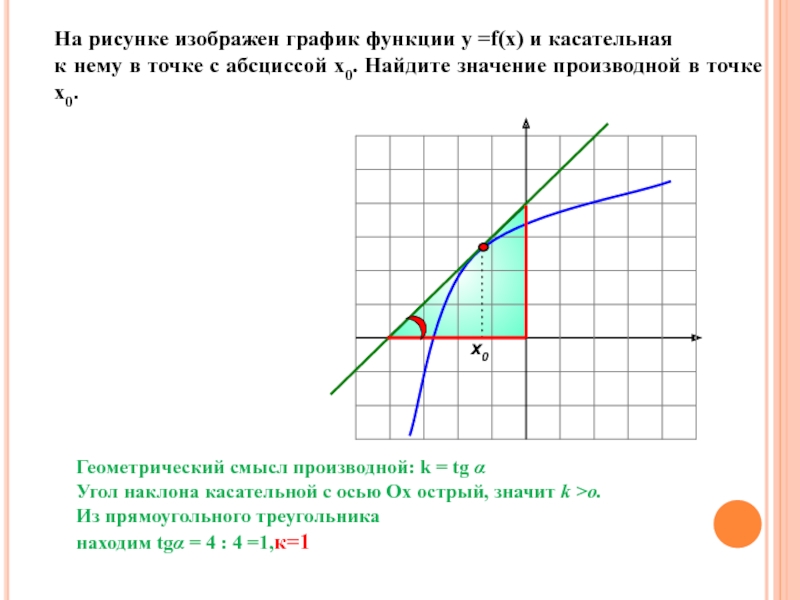
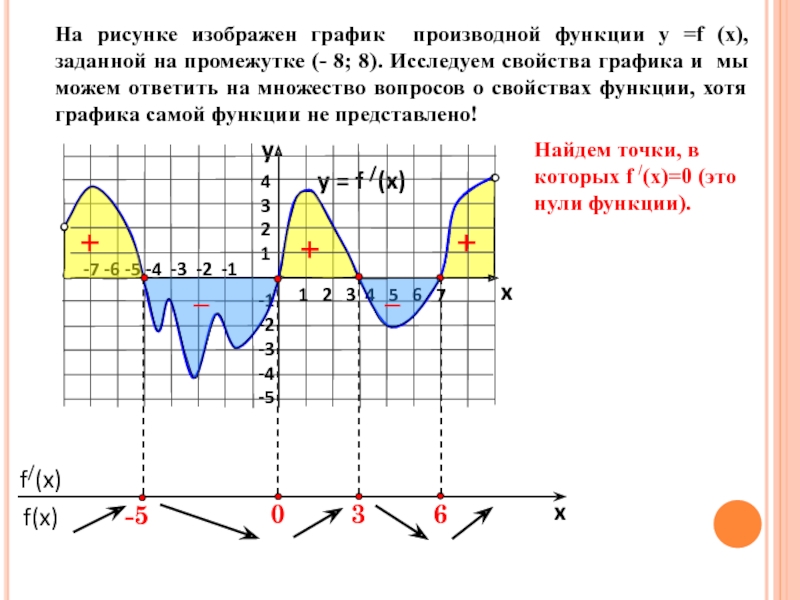
на промежутке (- 8; 8). Исследуем свойства графика и мы
можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено!y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
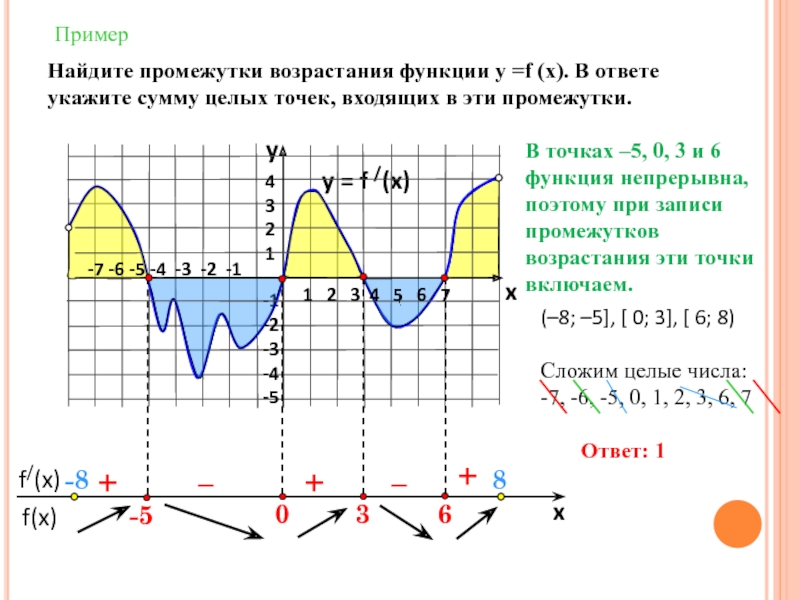
Найдем точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+

![задание 7. Применение производной к исследованию функций.
Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции у =f (x) на Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1]Ответ: xmax =](/img/thumbs/8cc18b5d6be0058f9c8b8a4dec16dfeb-800x.jpg)
![задание 7. Применение производной к исследованию функций.
Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума функции у =f (x) Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7]Ответ: 3.1](/img/thumbs/4ffecc1aa3b6eb60fecc7fb028860dd1-800x.jpg)

![задание 7. Применение производной к исследованию функций.
Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции у =f (x) принимает наибольшее значение?](/img/thumbs/e12c9d6d5cab1c4639233529e1b7d1ff-800x.jpg)
![задание 7. Применение производной к исследованию функций.
Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции у =f (x) принимает наименьшее значение?](/img/thumbs/c02684fc52c634c6b8e9dea0d6ed49fa-800x.jpg)
![задание 7. Применение производной к исследованию функций.
Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [ 0; 3] функции Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [ 0; 3] функции у =f (x) принимает наибольшее значение?](/img/thumbs/576146d4c843db834c30de6a780df90f-800x.jpg)
![задание 7. Применение производной к исследованию функций.
Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [ 1; 4] функции Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [ 1; 4] функции у =f (x) принимает наибольшее значение?](/img/thumbs/807cdcfe2a8f7790a74cd59a89dbe9c6-800x.jpg)
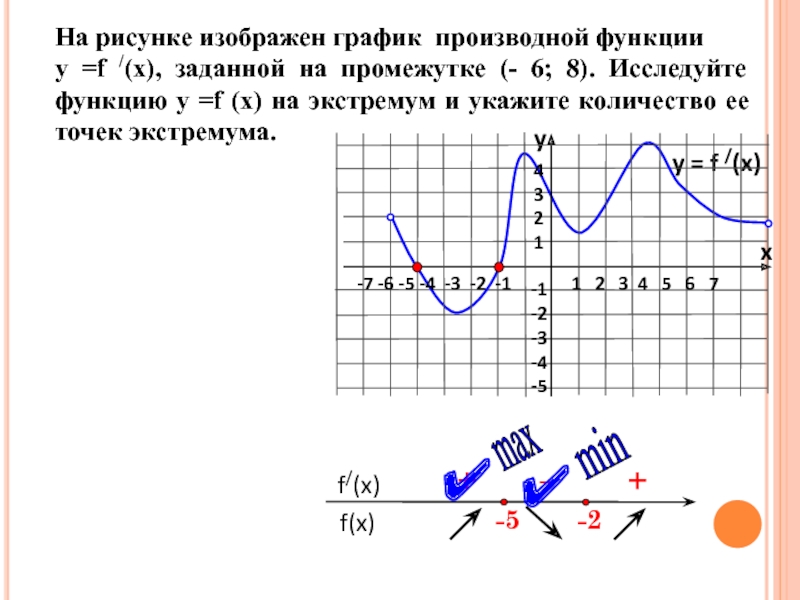
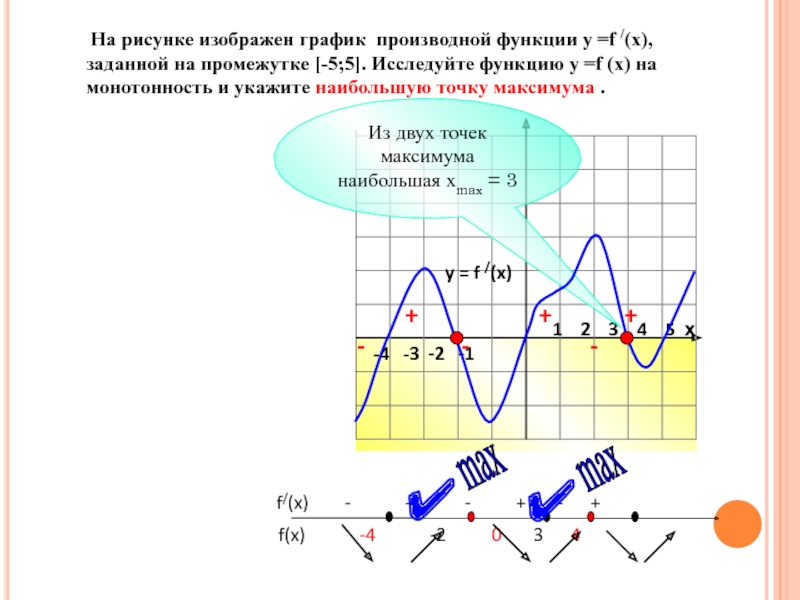
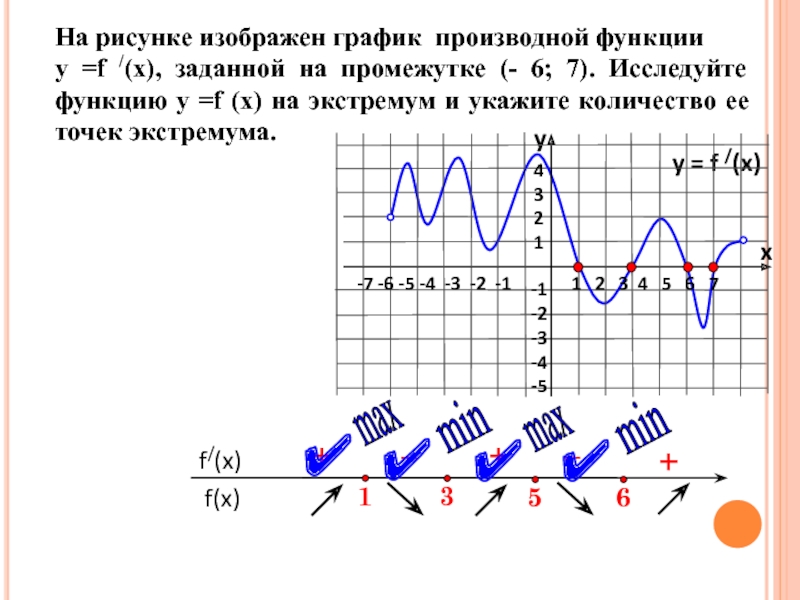
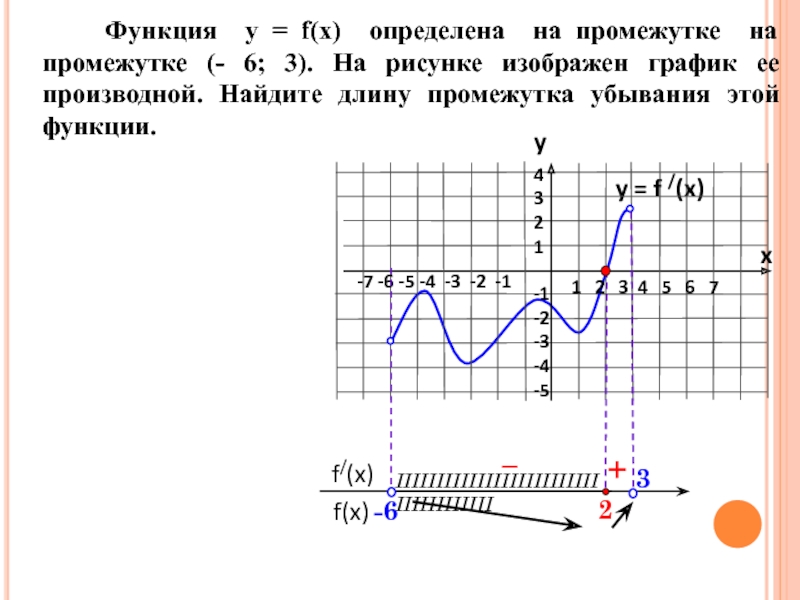
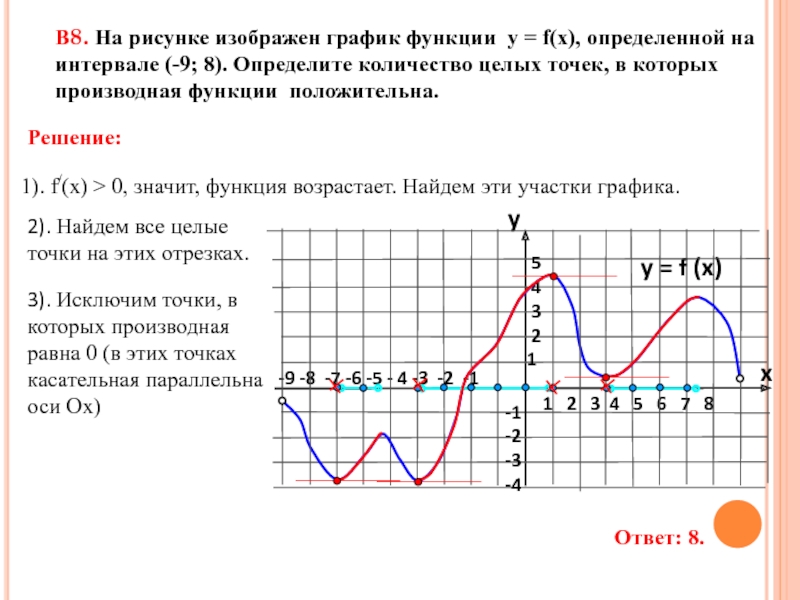
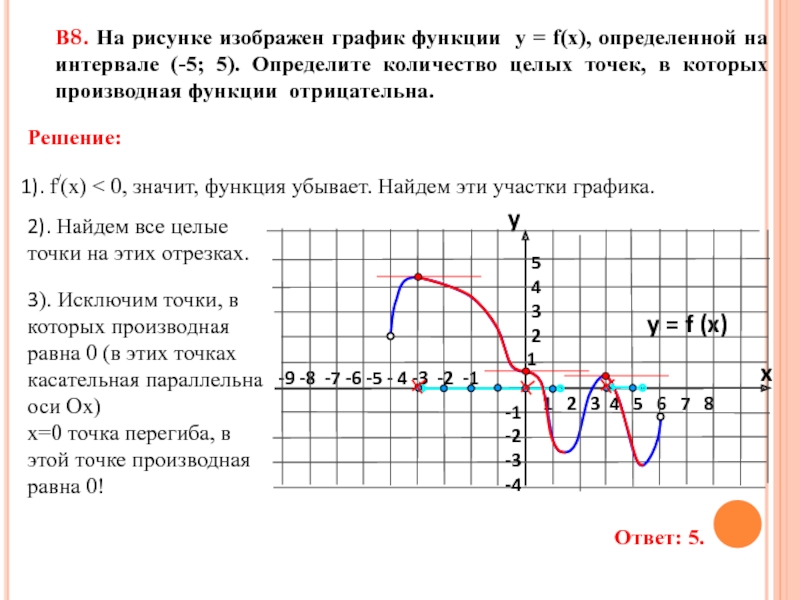
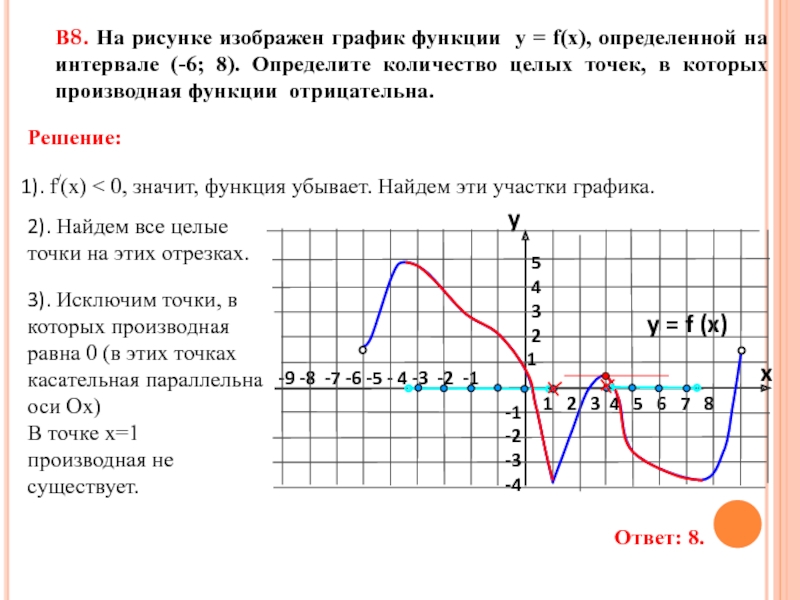
![задание 7. Применение производной к исследованию функций.
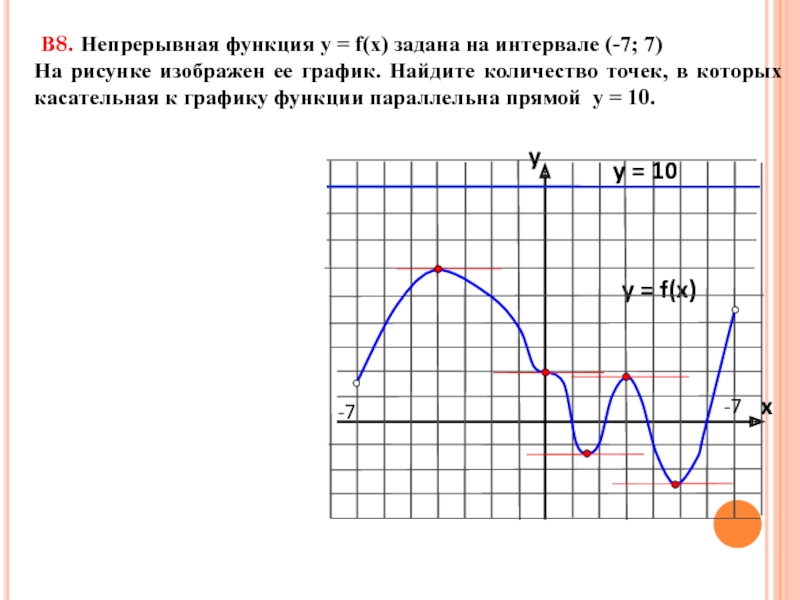
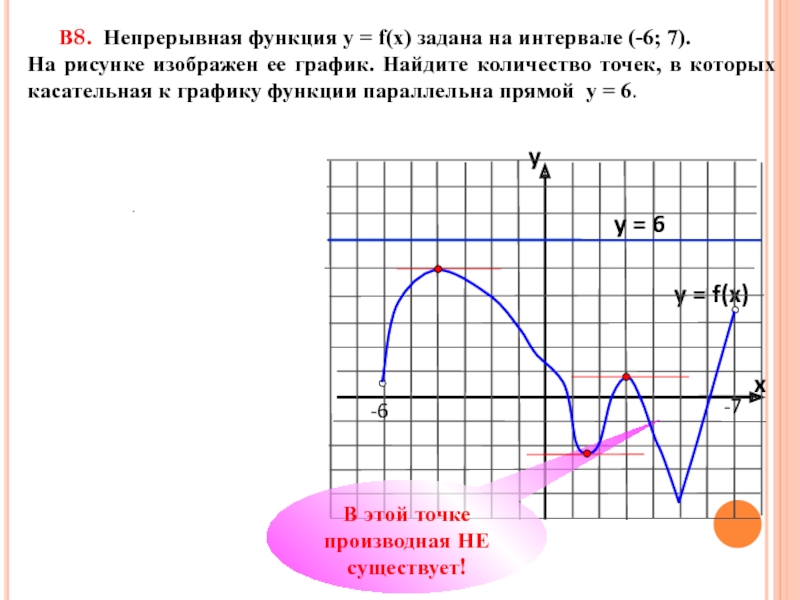
Готовимся к ЕГЭ В8. Непрерывная функция у = f(x) задана на отрезке [a;b] В8. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ее график.](/img/thumbs/b848d193e671b263bee72c48cbd9d4de-800x.jpg)