Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задание №1. Построить отрезок данной длины 3,75 см. Задание №2. Построить угол,
Содержание
- 1. Задание №1. Построить отрезок данной длины 3,75 см. Задание №2. Построить угол,
- 2. Слайд 2
- 3. Задачи на построениеТема урока:Учебная задача урока: дать
- 4. В геометрии выделяют задачи
- 5. O
- 6. Дано: отрезок АВ, луч ОС. Построили: OD=
- 7. АВСДано:Построили: угол О.Построение:окр.(А,r);окр.(А,r)
- 8. Дано: угол А.АПостроили: угол О.ВСОDEДоказать:
- 9. Дано: угол АПостроили: биссектрису АВПостроение:1.окр.(A,r);2.окр.(A,r)
- 10. Докажем, что луч АВ – биссектриса
- 11. Схема решения задач на построение:Анализ (рисунок искомой
- 12. Скачать презентанцию
Задачи на построениеТема урока:Учебная задача урока: дать представление о задачах на построение, этапах их решения и начать выделять основные задачи на построение.
Слайды и текст этой презентации
Слайд 1Задание №1.
Построить отрезок данной длины 3,75 см.
Задание №2.
Построить угол,
данный величины 22˚30.
Слайд 3Задачи на построение
Тема урока:
Учебная задача урока:
дать представление о задачах
на построение, этапах их решения и начать выделять основные задачи
на построение.
Слайд 4 В геометрии выделяют задачи на построение, которые
можно решить только с помощью двух инструментов: циркуля и линейки
без масштабных делений.Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Слайд 5O D
C
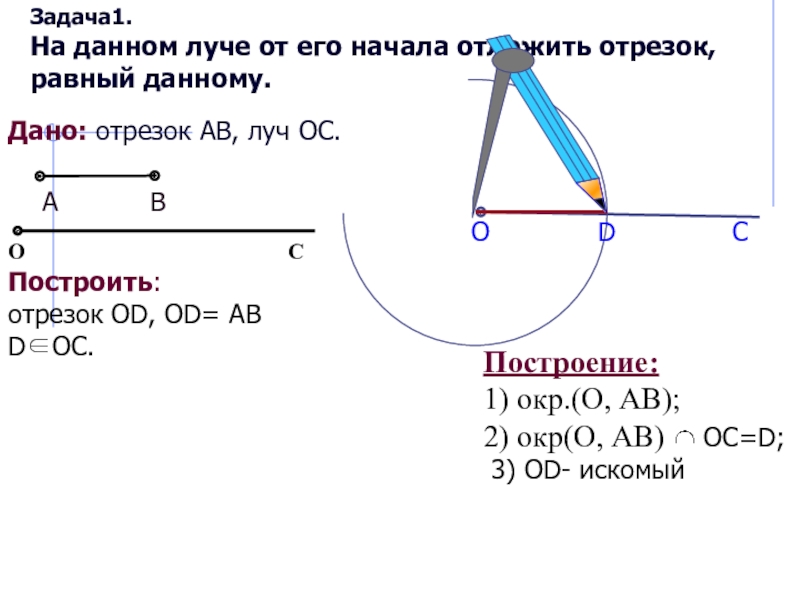
Дано: отрезок АВ, луч
ОС. Построить:
отрезок OD, OD= АВ DОС.
Построение:
1) окр.(O, АВ);
2) окр(O, АВ) OC=D;
3) OD- искомый
Задача1.
На данном луче от его начала отложить отрезок, равный данному.
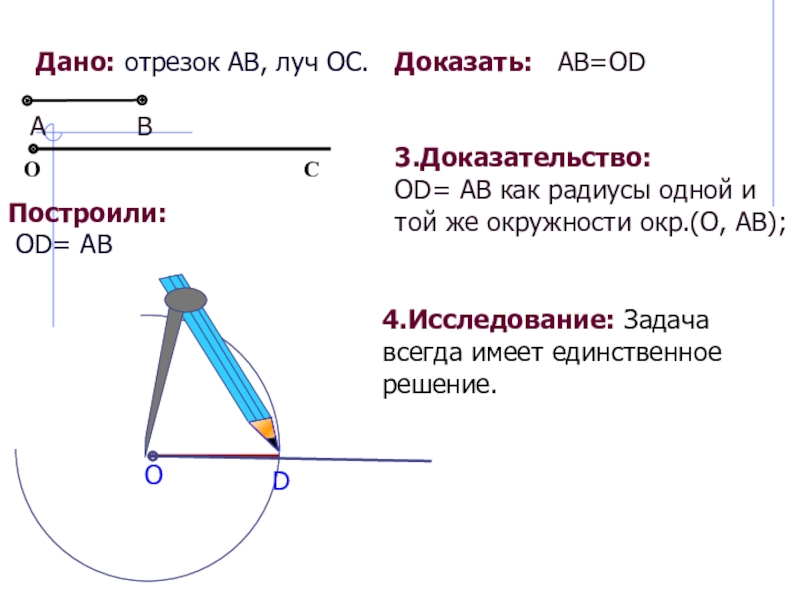
Слайд 6Дано: отрезок АВ, луч ОС.
Построили:
OD= АВ
Доказать:
АB=ОD
3.Доказательство:
OD= АВ как радиусы одной и той же
окружности окр.(O, АВ); 4.Исследование: Задача всегда имеет единственное решение.
Слайд 7А
В
С
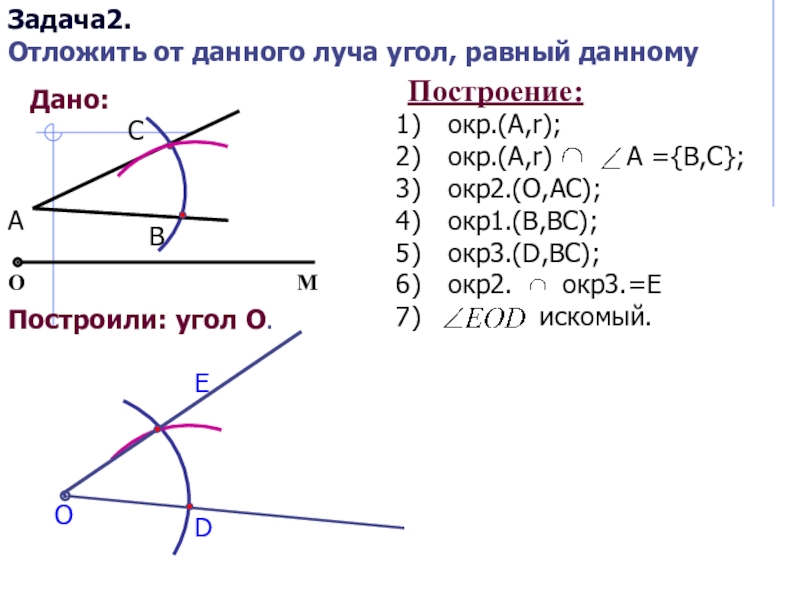
Дано:
Построили: угол О.
Построение:
окр.(А,r);
окр.(А,r) А ={В,С};
окр2.(O,AC);
окр1.(B,BC);
окр3.(D,BC);
окр2. окр3.=E
искомый.
О
D
E
Задача2.
Отложить от данного луча угол, равный данному
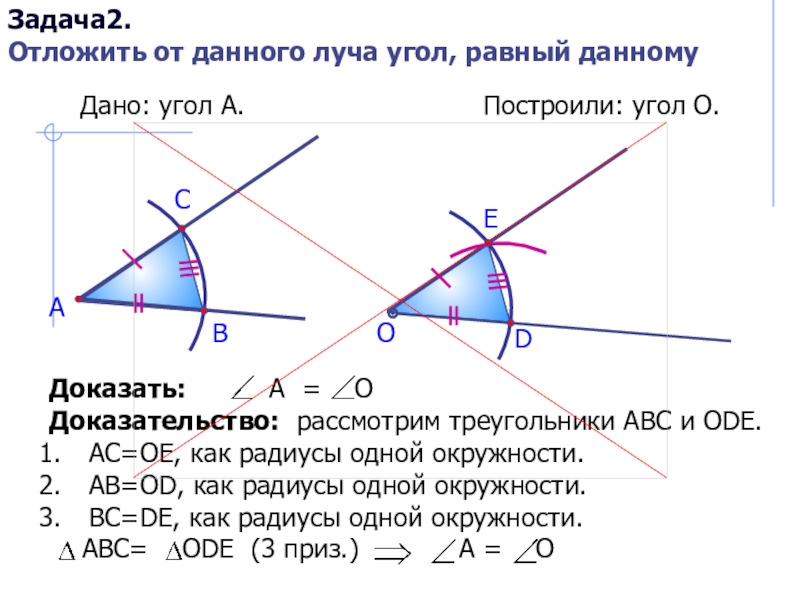
Слайд 8Дано: угол А.
А
Построили: угол О.
В
С
О
D
E
Доказать: А
= О
Доказательство: рассмотрим треугольники АВС и ОDE.
АС=ОЕ, как радиусы
одной окружности.АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
Задача2.
Отложить от данного луча угол, равный данному
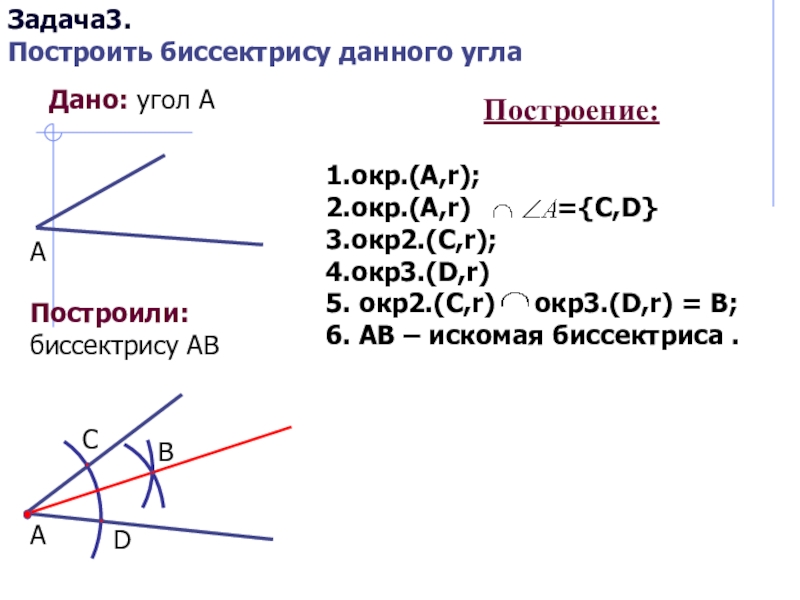
Слайд 9Дано: угол А
Построили: биссектрису АВ
Построение:
1.окр.(A,r);
2.окр.(A,r)
={C,D}
3.окр2.(C,r);
4.окр3.(D,r)
5. окр2.(C,r) окр3.(D,r) = B;
6. AB – искомая
биссектриса .А
D
C
B
Задача3.
Построить биссектрису данного угла
Слайд 10Докажем, что луч АВ – биссектриса А
3. Доказательство:
Дополнительное
построение (соединим точку В с точками D и C) .
Рассмотрим
∆ АСВ и ∆ АDB:А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса
4.Исследование: Задача всегда имеет единственное решение.
Слайд 11Схема решения задач на построение:
Анализ (рисунок искомой фигуры, установление связей
между заданными и искомыми элементами, план построения).
Построение по намеченному
плану.Доказательство, что данная фигура удовлетворяет условиям задачи.
Исследование (когда и сколько задача имеет решений?).
