Закон преломления и отражения света (закон Снеллиуса)

однородных, изотропных, электрически нейтральных, непроводящих сред.
Из

среды 1 с ε = ε1 на границу раздела со средой 2, диэлектрическая проницаемость которой равна ε2, под произвольным углом падает световая (электромагнитная) волна.
1. Как изменится направление распространения волны при отражении от границы раздела?
2. Как изменится направление распространения волны при прохождении через границу раздела?

границу раздела под произвольным углом.
- углы, которые образует направление распространения

падающей волны с осями OX, OY, OZ соответственно.

- углы, которые образуют направления распространения отражённой и прошедшей волн с осями OX, OY, OZ соответственно.

Систему координат выберем так, чтобы падающая волна распространялась в плоскости XZ,

условий для напряжённости электрического поля, на границе раздела двух сред

тангенциальные составляющие напряжённости электрического поля сохраняются.

В нашем случае напряжённость поля в первой среде складывается из напряжённости поля падающей волны и напряжённости поля отражённой волны, а напряжённость поля во второй среде – из напряжённости поля прошедшей волны.

и прошедшей волн:
Условие равенства тангенциальных составляющих напряжённостей полей:
На границе раздела

это равенство должно выполняться в любой момент времени, поэтому

если в любой точке плоскости раздела (x = 0).
Падающий, отражённый

и преломлённый лучи лежат в одной плоскости.

отражения.
Отношение синуса угла падения к синусу угла преломления равно относительному

показателю преломления двух сред.

лучи лежат в одной плоскости. Угол падения равен углу отражения.

Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления двух сред.

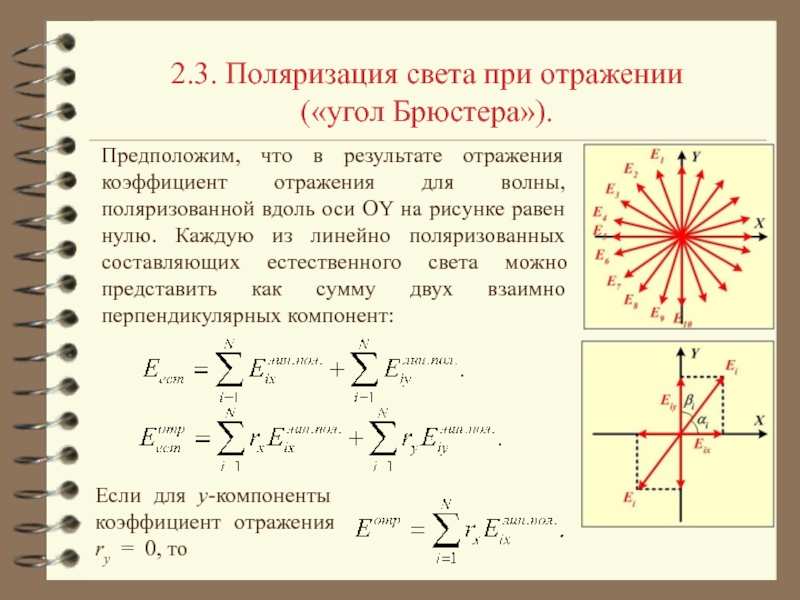
стекла, если отраженный и преломленный лучи образуют между собой прямой

угол? Скорость света в стекле v =2·108 м/с.

Задача. На какой глубине под водой находится водолаз, если он видит отраженными от поверхности воды те части горизонтального дна, которые расположены от него на расстоянии 15 м и больше. Рост водолаза 1,7 м. Показатель преломления воды n = 1,33.
Задача. Луч света падает на стеклянную пластинку с показателем преломления n = 1,7 под углом, для которого sin = 0,8. Вышедший из пластинки луч оказался смещенным относительно падающего на расстояние b = 2 см. Какова толщина h пластинки ?
Задача. На поверхности озера, имеющего глубину Н = 2 м, плавает круглый плот радиуса r = 8 м. Найти радиус полной тени от плота на дне озера при освещении рассеянным светом. Показатель преломления воды n = 1,33.
Задача. Каким должен быть радиус внешнего изгиба световода R, изготовленного из вещества с показателем преломления n = 1,5, чтобы при диаметре световода d = 5 мм, свет, вошедший в световод перпендикулярно плоскости его поперечного сечения, распространялся, не выходя из световода?

границу раздела падает волна такой поляризации, что вектор напряжённости электрического

поля лежит в плоскости падения (плоскость XY на рисунке).

На границе раздела выполняются граничные условия для векторов напряжённостей полей, а также векторов электрической и магнитной индукции.

среде – падающая и отражённая волна, во второй – прошедшая

волна. Для вектора E:

Для вектора H:

связаны соотношением
Второе уравнение системы

= 1)
Перепишем систему уравнений, учтём, что α = γ:

из тригонометрии:

напряжённости, умноженной на показатель преломления, поэтому коэффициент отражения для волны

с такой поляризацией будет равен

имеет особенность при x = π/2. В этом случае она

стремится к бесконечности.

При α + β = π/2 знаменатель дроби стремится к бесконечности, а R стремится к нулю.

Это означает, что волна с такой поляризацией, когда вектор E лежит в плоскости падения и перпендикулярен плоскости раздела сред в отражённом свете не существует при α + β = π/2.

такой поляризацией, когда вектор E лежит в плоскости раздела сред

и перпендикулярен плоскости падения. Для такой волны граничные условия для векторов E и H можно записать так:

Перепишем систему уравнений, учтём, что α = γ:

связаны соотношением
Второе уравнение системы

= 1)

не имеет особенности при x = π/2. При α +

β = π/2 знаменатель дроби равен единице.

Это означает, что волна с такой поляризацией, когда вектор E лежит в плоскости раздела и перпендикулярен плоскости падения сред существует в отражённом свете не при α + β = π/2.

светом при падении на поверхность под таким углом?
Если колебания

вектора напряжённости электрического поля в волне происходят в одной плоскости, волна называется линейно поляризованной.

Естественный (неполяризованный) свет можно представить, как сумму очень большого (возможно, бесконечного) числа линейно поляризованных волн (см. рисунок) с различной поляризацией.

отражения коэффициент отражения для волны, поляризованной вдоль оси OY на

рисунке равен нулю. Каждую из линейно поляризованных составляющих естественного света можно представить как сумму двух взаимно перпендикулярных компонент:

Если для y-компоненты коэффициент отражения ry = 0, то

превратится в линейно (или плоско) поляризованный.
Если естественный свет падает

на поверхность раздела двух сред, то в случае, когда сумма угла падения и угла отражения равна α + β = π/2, отражённая волна линейно поляризована так, что вектор E лежит в плоскости раздела сред и перпендикулярен плоскости падения.

Угол падения α, при котором сумма угла падения и угла отражения равна α + β = π/2, а отражённая волна линейно поляризована так, что вектор E лежит в плоскости раздела сред и перпендикулярен плоскости падения, называется углом Брюстера.

углом Брюстера α + β = π/2, угол падения равен

углу отражения, следовательно (см. рисунок) отражённый и прошедший лучи взаимно перепндикулярны.

Из закона Снеллиуса: