(величина и направление F может меняться с течением времени).
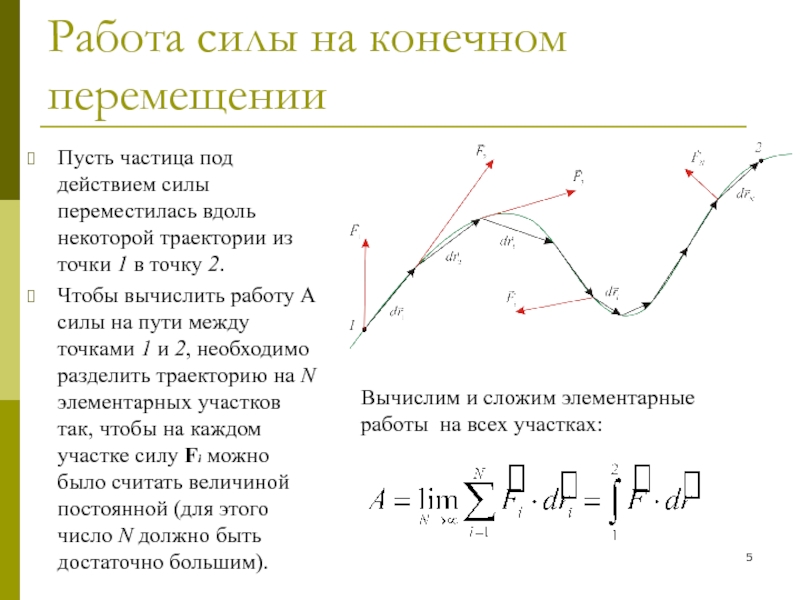
Пусть частица
совершила элементарное перемещение dr за промежуток времени dt, в течение которого силу F можно считать постоянной.Элементарной работой δA силы F называется скалярное произведение вектора силы на вектор dr элементарного перемещения :