Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
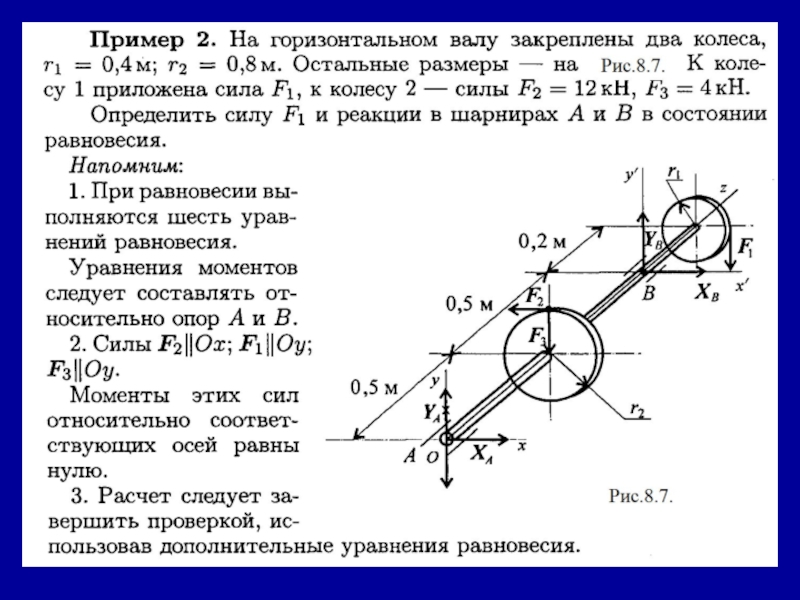
Занятие 6. (2 часа) Балочные системы. Определение реакций опор и моментов
Содержание
- 1. Занятие 6. (2 часа) Балочные системы. Определение реакций опор и моментов
- 2. 6.1. Виды нагрузок и разновидности опор6.1.1. Виды
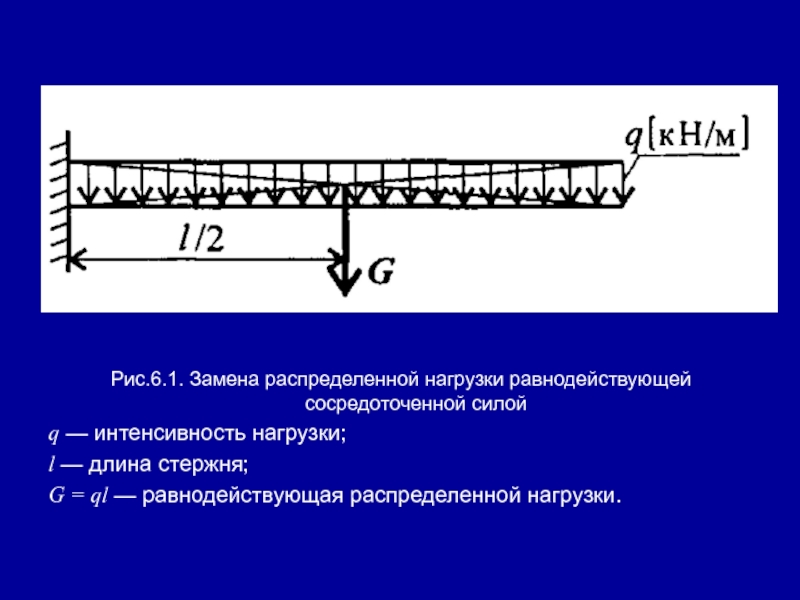
- 3. Рис.6.1. Замена распределенной нагрузки равнодействующей сосредоточенной силойq
- 4. 6.1.2. Разновидности опор балочных систем (см.занятие 1)
- 5. Для определения этих неизвестных удобно использовать систему
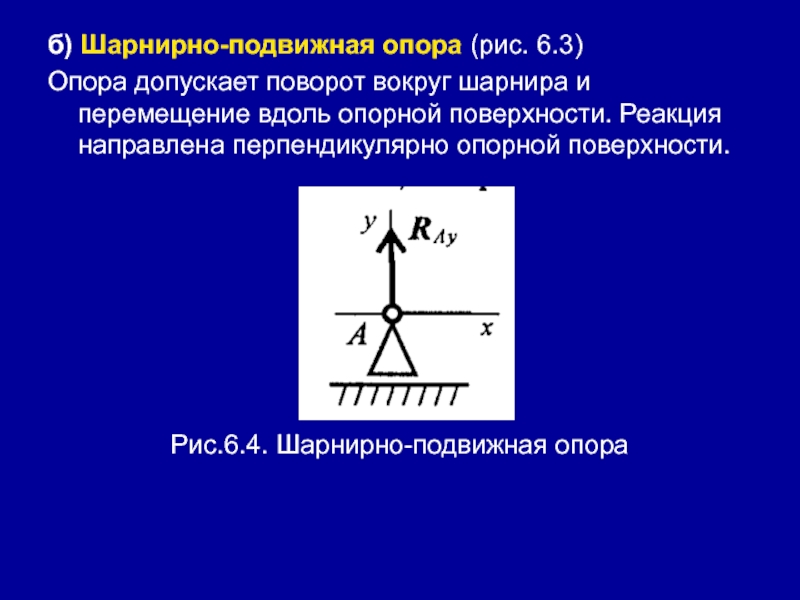
- 6. б) Шарнирно-подвижная опора (рис. 6.3)Опора допускает поворот
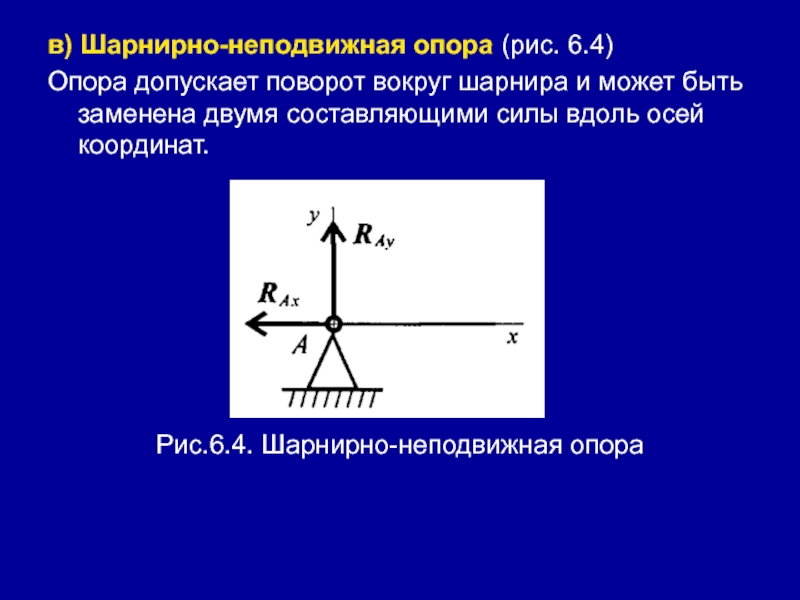
- 7. в) Шарнирно-неподвижная опора (рис. 6.4)Опора допускает поворот
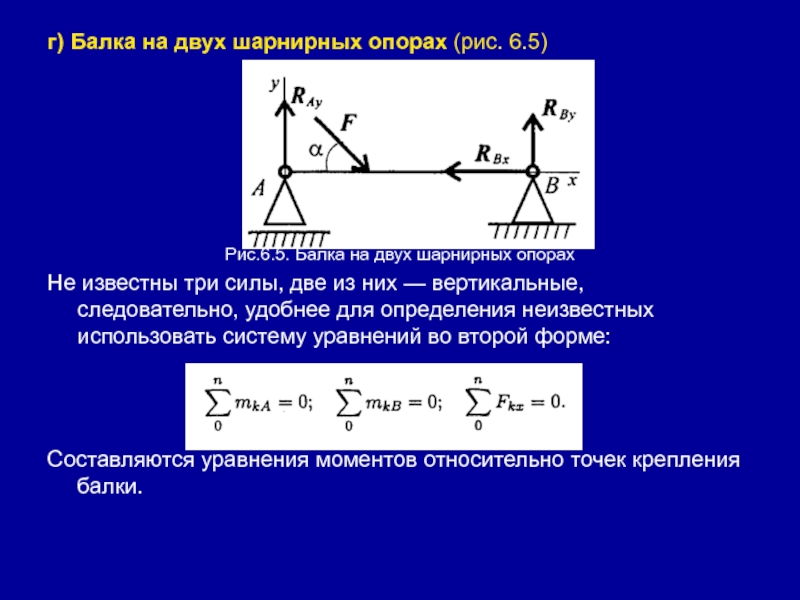
- 8. г) Балка на двух шарнирных опорах (рис.
- 9. Поскольку момент силы, проходящей через точку крепления,
- 10. При равновесии твердого тела, где можно выбрать
- 11. 6.2. Примеры решения задачПример 1. Одноопорная (защемленная)
- 12. Замечание. Если направления выбраны неверно, при расчетах
- 13. Знаки полученных реакций (+), следовательно, направления реакций выбраны верно.
- 14. 3. Для проверки правильности решения составляем уравнение моментов относительно точки В.
- 15. Пример 2. Двухопорная балка с шарнирными опорами
- 16. Решение:1. Левая опора (точка А) — подвижный
- 17. Сосредоточенную силу помещаем в середине пролета, далее
- 18. Слайд 18
- 19. Слайд 19
- 20. Занятие 7. (2 часа) Контрольная работа №1
- 21. Занятие 8. (2 часа) Пространственная система сил. Центр тяжести.
- 22. 8.1. Момент силы относительно оси.Момент силы относительно
- 23. Момент считаем положительным, если сила разворачивает тело
- 24. 8.2. Пространственная сходящаяся система сил.а) вектор в
- 25. б) Пространственная сходящаяся система силПространственная сходящаяся система
- 26. Совмещаем начало координат с точкой пересечения линий
- 27. Слайд 27
- 28. в) Произвольная пространственная система силПриведение произвольной пространственной
- 29. Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 8.5в).
- 30. Обычно суммарный момент раскладывают на составляющие: три
- 31. г) Уравнения равновесия пространственной системы силПри
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. 8.3. Сила тяжести.Сила тяжести — равнодействующая сил
- 38. 8.4. Точка приложения силы тяжести.Для определения точки
- 39. Тело состоит из частей, силы тяжести которых
- 40. Слайд 40
- 41. Слайд 41
- 42. 8.4. Центр тяжести однородных плоских тел (плоских
- 43. Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
- 44. 8.5. Определение координат центра тяжести плоских фигурПримечание.
- 45. При решении задач используются следующие методы:1) метод
- 46. Слайд 46
- 47. Рис.8.12. Составное сечение из листа и прокатных профилей.
- 48. Слайд 48
- 49. Занятие 9. (2 часа) Основные понятия кинематики
- 50. 9.1.Основные кинематические параметры а) ТраекторияЛинию, которую очерчивает
- 51. в) Уравнение движения точкиУравнение, определяющее положение движущейся
- 52. Таким образом, уравнение движения можно представить в
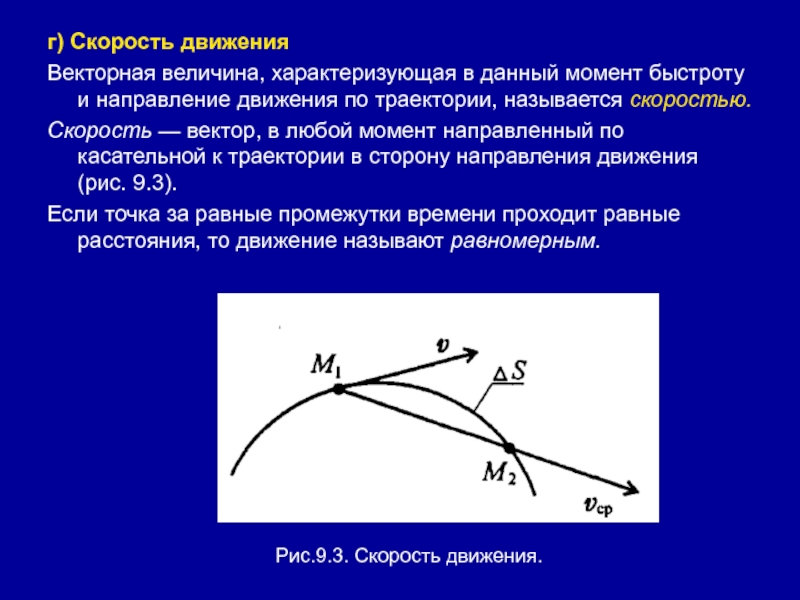
- 53. г) Скорость движенияВекторная величина, характеризующая в данный
- 54. Средняя скорость на пути AS определяется какгде
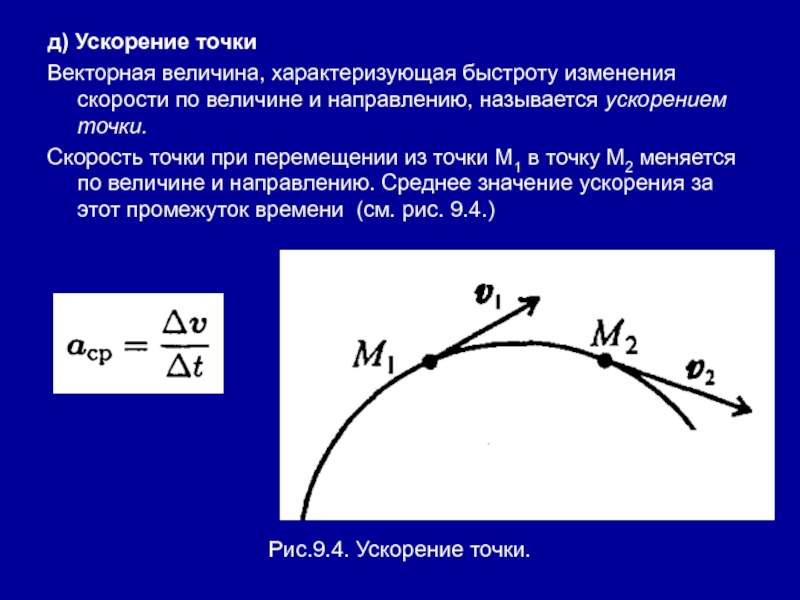
- 55. д) Ускорение точкиВекторная величина, характеризующая быстроту изменения
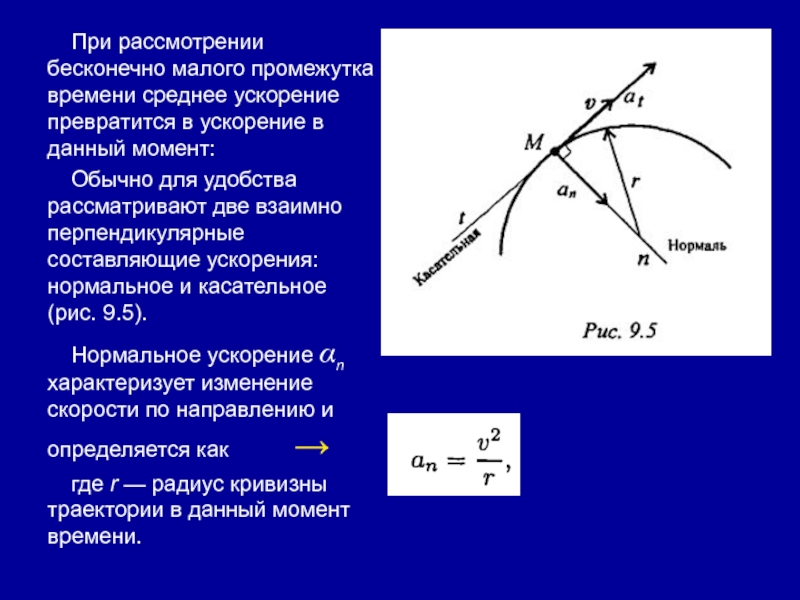
- 56. При рассмотрении бесконечно малого промежутка времени среднее
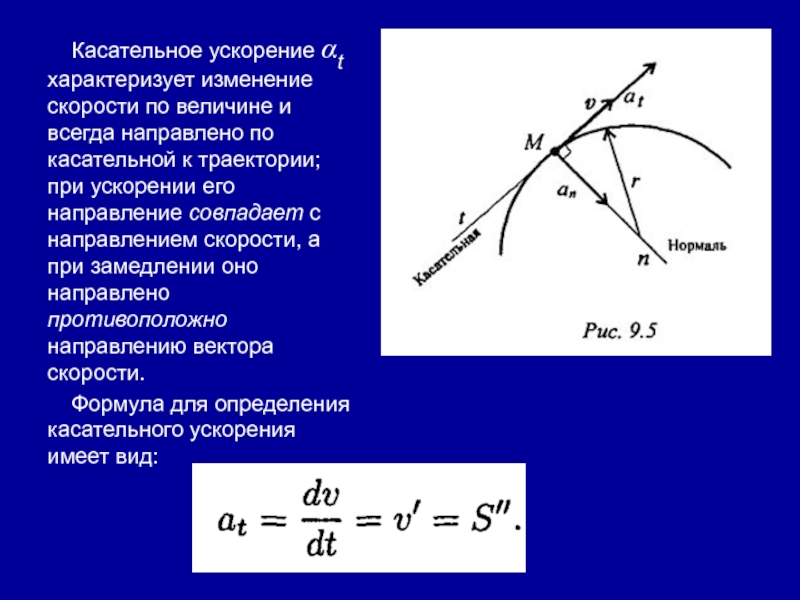
- 57. Касательное ускорение αt характеризует изменение скорости по
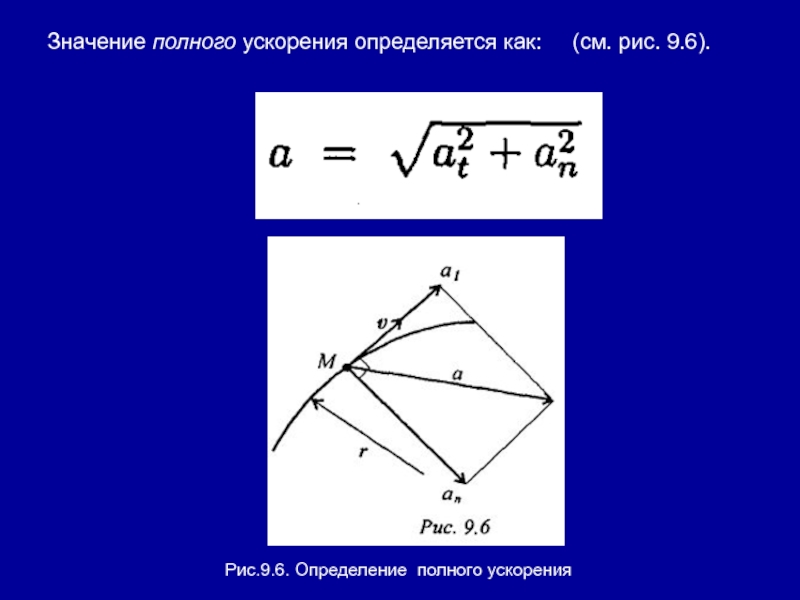
- 58. Значение полного ускорения определяется как: (см. рис. 9.6).Рис.9.6. Определение полного ускорения
- 59. Слайд 59
- 60. Слайд 60
- 61. Слайд 61
- 62. Скачать презентанцию
6.1. Виды нагрузок и разновидности опор6.1.1. Виды нагрузокПо способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.Часто нагрузка
Слайды и текст этой презентации
Слайд 26.1. Виды нагрузок и разновидности опор
6.1.1. Виды нагрузок
По способу приложения
нагрузки делятся на сосредоточенные и распределенные.
Если реально передача нагрузки
происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой
(рис. 6.1).
Слайд 3Рис.6.1. Замена распределенной нагрузки равнодействующей сосредоточенной силой
q — интенсивность нагрузки;
l
— длина стержня;
G = ql — равнодействующая распределенной нагрузки.
Слайд 46.1.2. Разновидности опор балочных систем (см.занятие 1)
Балка — конструктивная
деталь в виде прямого бруса, закрепленная на опорах и изгибаемая
приложенными к ней силами.Высота сечения балки незначительна по сравнению с длиной.
а) Жесткая заделка (защемление) (рис. 6.2)
Рис.6.2. Жесткая заделка (защемление)
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы RАx и RAy и парой с моментом МR.
Слайд 5Для определения этих неизвестных удобно использовать систему уравнений в виде
Каждое
уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля
правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например В: 
Слайд 6б) Шарнирно-подвижная опора (рис. 6.3)
Опора допускает поворот вокруг шарнира и
перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Рис.6.4. Шарнирно-подвижная
опора
Слайд 7в) Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и
может быть заменена двумя составляющими силы вдоль осей координат.
Рис.6.4.
Шарнирно-неподвижная опора
Слайд 8г) Балка на двух шарнирных опорах (рис. 6.5)
Рис.6.5. Балка на
двух шарнирных опорах
Не известны три силы, две из них —
вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:Составляются уравнения моментов относительно точек крепления балки.
Слайд 9Поскольку момент силы, проходящей через точку крепления, равен 0, в
уравнении останется одна неизвестная сила.
Для контроля правильности решения используется дополнительное
уравнение:
Слайд 10При равновесии твердого тела, где можно выбрать три точки, не
лежащие на одной прямой, удобно использовать систему уравнений в третьей
форме (рис. 6.6):
Слайд 116.2. Примеры решения задач
Пример 1. Одноопорная (защемленная) балка нагружена сосредоточенными
силами и парой сил (рис. 6.7). Определить реакции заделки.
Решение:
1. В
заделке может возникнуть реакция, представляемая двумя составляющими (RАу, RАx), и реактивный момент МА. Наносим на схему балки возможные направления реакций.
Слайд 12Замечание.
Если направления выбраны неверно, при расчетах получим отрицательные значения
реакций. В этом случае реакции на схеме следует направить в
противоположную сторону, не повторяя расчета.В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке.
Для решения удобно использовать систему уравнений равновесия в первой форме.
Каждое уравнение будет содержать одну неизвестную.
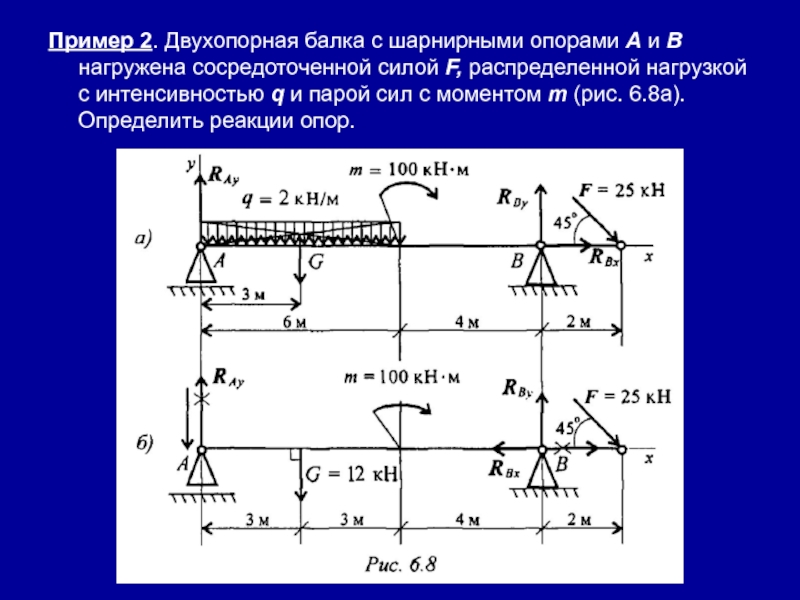
Слайд 15Пример 2. Двухопорная балка с шарнирными опорами А и В
нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и
парой сил с моментом т (рис. 6.8а). Определить реакции опор.
Слайд 16Решение:
1. Левая опора (точка А) — подвижный шарнир, здесь реакция
направлена перпендикулярно опорной поверхности.
Правая опора (точка В) — неподвижный шарнир,
здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно.
3. Заменяем распределенную нагрузку сосредоточенной:
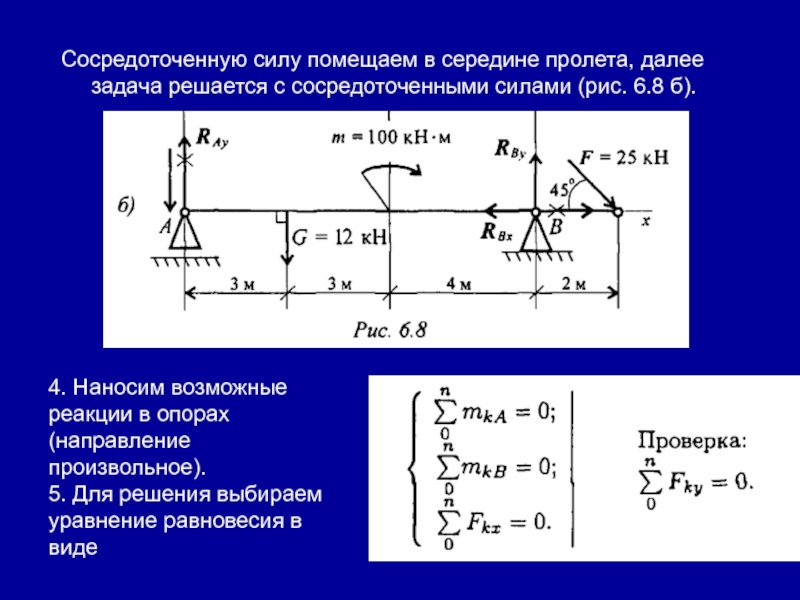
Слайд 17Сосредоточенную силу помещаем в середине пролета, далее задача решается с
сосредоточенными силами (рис. 6.8 б).
4. Наносим возможные реакции в опорах
(направление произвольное).5. Для решения выбираем уравнение равновесия в виде
Слайд 228.1. Момент силы относительно оси.
Момент силы относительно оси равен моменту
проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси
с плоскостью (рис. 8.1а).Moo(F) = пр Fα,
α — расстояние от оси до проекции F;
npF — проекция силы на плоскость, перпендикулярную оси ОО.
npF = F cos α; MОО(F) = F cos α ∙ α.
Рис.8.1. Момент силы относительно оси.
Слайд 23
Момент считаем положительным, если сила разворачивает тело по часовой стрелке.
Смотреть со стороны положительного направления оси.
Если линия действия силы пересекает
ось или линия действия силы параллельна оси, моменты силы относительно этой оси равны нулю (рис. 8.1б).Силы и ось лежат в одной плоскости, они не смогут повернуть тело вокруг этой оси.
F1 пересекает ось; MОО(F1) = 0;
F2||ОО- npF2 = 0; MOO(F2) = 0.
Слайд 248.2. Пространственная сходящаяся система сил.
а) вектор в пространстве.
В пространстве вектор
силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора
образуют ребра прямоугольного параллелепипеда, вектор силы совпадает с диагональю (рис. 8.2).Рис.8.2. Вектор в пространстве.
Модуль вектора может быть
получен из зависимости
αх, αу, αz — углы между вектором осями координат.
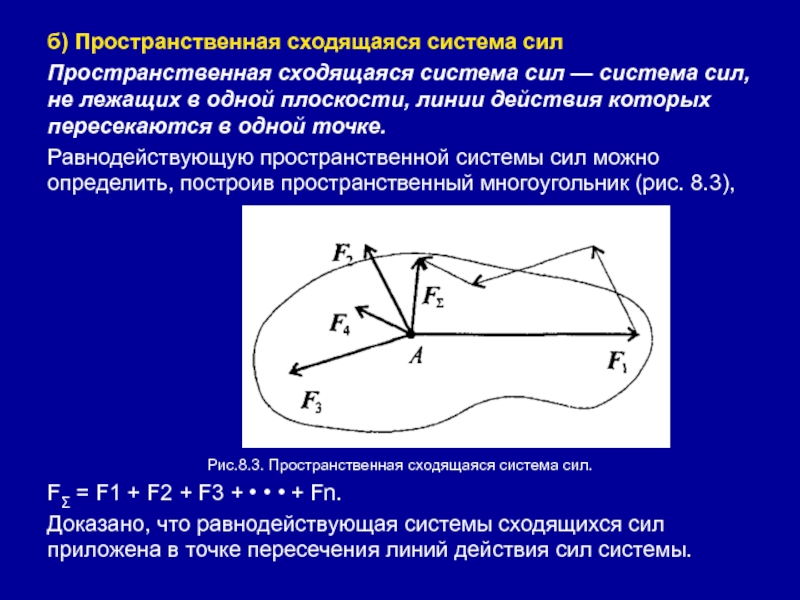
Слайд 25б) Пространственная сходящаяся система сил
Пространственная сходящаяся система сил — система
сил, не лежащих в одной плоскости, линии действия которых пересекаются
в одной точке.Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 8.3),
Рис.8.3. Пространственная сходящаяся система сил.
FΣ = F1 + F2 + F3 + • • • + Fn.
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Слайд 26Совмещаем начало координат с точкой пересечения линий действия сил системы.
Проецируем все силы на оси координат и суммируем соответствующие проекции
(рис.
8.4). Рис.8.4. Проекции равнодействующей на оси координат
Получим проекции равнодействующей на оси координат:
Слайд 28в) Произвольная пространственная система сил
Приведение произвольной пространственной системы сил к
центру О
Дана пространственная система сил (рис. 8.5а). Приведем ее к
центру О.рис. 8.5а
Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения
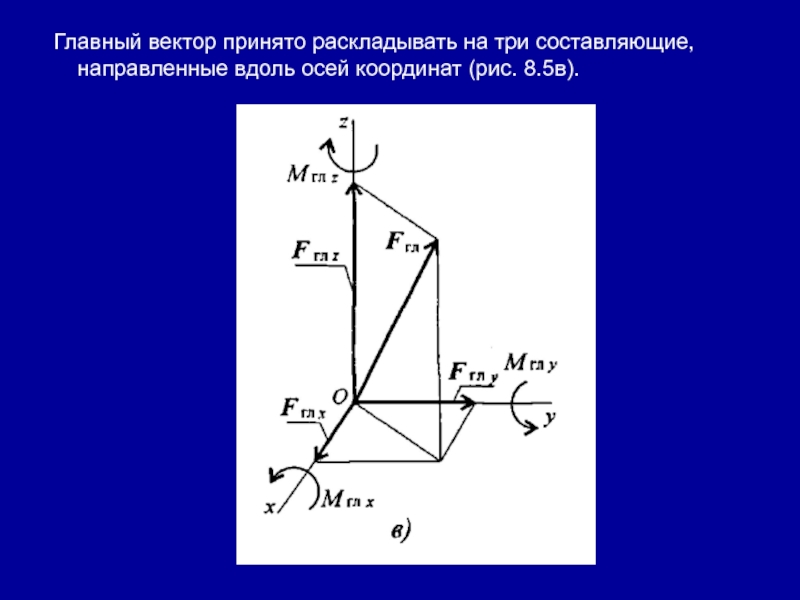
Слайд 29 Главный вектор принято раскладывать на три составляющие, направленные вдоль
осей координат (рис. 8.5в).
Слайд 30Обычно суммарный момент раскладывают на составляющие: три момента относительно осей
координат.
Абсолютное значение главного вектора (рис. 8.56) равно
Слайд 31г) Уравнения равновесия пространственной системы сил
При равновесии Fгл =
0; Мгл = 0.
Получаем шесть уравнений равновесия:
Шесть уравнений равновесия
пространственной системы сил соответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей.
Слайд 378.3. Сила тяжести.
Сила тяжести — равнодействующая сил притяжения к Земле,
она распределена по всему объему тела. Силы притяжения, приложенные к
частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.8). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.Рис.8.8. Сила тяжести.
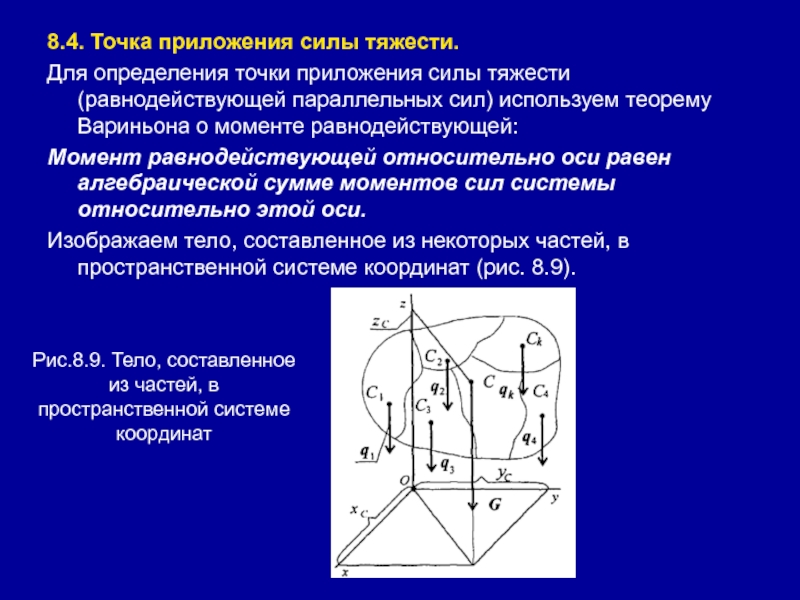
Слайд 388.4. Точка приложения силы тяжести.
Для определения точки приложения силы тяжести
(равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей
относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.9).
Рис.8.9. Тело, составленное из частей, в пространственной системе координат
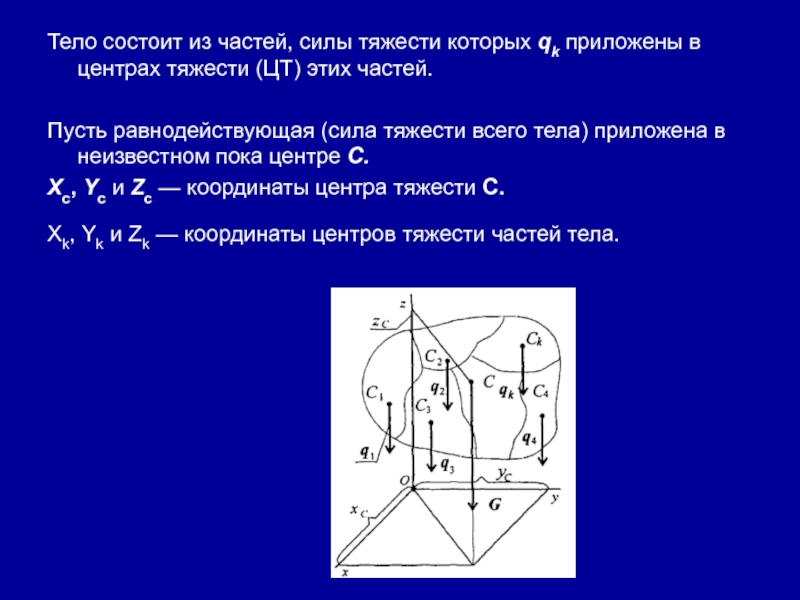
Слайд 39Тело состоит из частей, силы тяжести которых qk приложены в
центрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела)
приложена в неизвестном пока центре С.Xc, Yс и Zc — координаты центра тяжести С.
Xk, Yk и Zk — координаты центров тяжести частей тела.
Слайд 428.4. Центр тяжести однородных плоских тел (плоских фигур)
Очень часто приходится
определять центр тяжести различных плоских тел и геометрических плоских фигур
сложной формы.Для плоских тел можно записать:
V = Ah,
где А — площадь фигуры, h — ее высота.
Тогда после подстановки в записанные выше формулы получим:
Слайд 43
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент
относительно центральной оси равен нулю.
Слайд 448.5. Определение координат центра тяжести плоских фигур
Примечание. Центр тяжести симметричной
фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине
высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.10) :
а) — круг; б) — квадрат, прямоугольник; в) — треугольник;
г) — полукруг).
Рис.8.10. Определение координат центра тяжести плоских фигур
Слайд 45При решении задач используются следующие методы:
1) метод симметрии: центр тяжести
симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения
разделяем на несколько простых частей, положение центров тяжести которых легко определить;3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Слайд 509.1.Основные кинематические параметры
а) Траектория
Линию, которую очерчивает материальная точка при
движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой,
плоской и пространственной линией.Уравнение траектории при плоском движении: у = f(x).
б) Пройденный путь
Путь измеряется вдоль траектории в направлении движения. Обозначение — s, единицы измерения — метры.
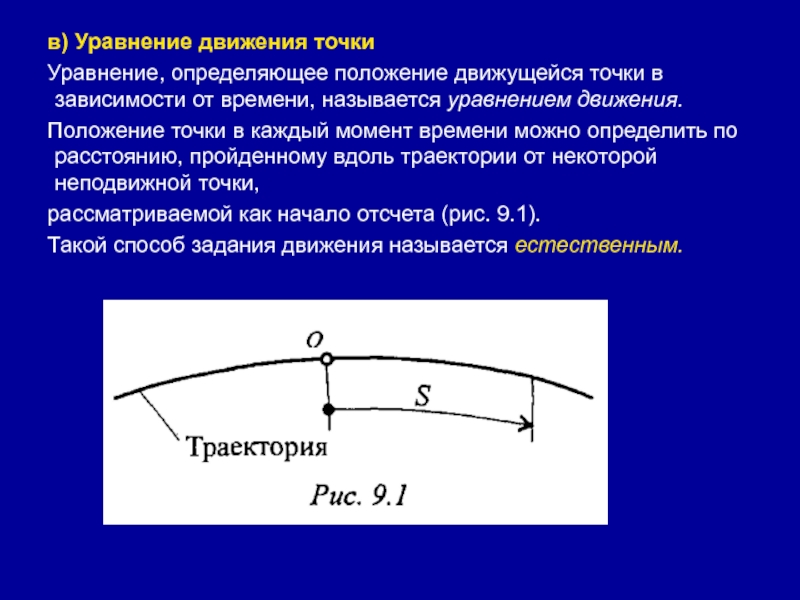
Слайд 51в) Уравнение движения точки
Уравнение, определяющее положение движущейся точки в зависимости
от времени, называется уравнением движения.
Положение точки в каждый момент времени
можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки, рассматриваемой как начало отсчета (рис. 9.1).
Такой способ задания движения называется естественным.
Слайд 52Таким образом, уравнение движения можно представить в виде
S =
f (t).
Положение точки можно также определить, если известны ее
координаты в зависимости от времени(рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения:
В случае пространственного движения добавляется и третья координата
z = f3(t)
Такой способ задания движения называют координатным.
Слайд 53г) Скорость движения
Векторная величина, характеризующая в данный момент быстроту и
направление движения по траектории, называется скоростью.
Скорость — вектор, в любой
момент направленный по касательной к траектории в сторону направления движения (рис. 9.3).Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным.
Рис.9.3. Скорость движения.
Слайд 54Средняя скорость на пути AS определяется как
где ΔS — пройденный
путь за время Δt;
Δt — промежуток времени.
Если точка за
равные промежутки времени проходит неравные "пути, то движение называют неравномерным.В этом случае скорость — величина переменная и зависит от времени v = f(t).
При рассмотрении малых промежутков времени (Δt → 0) средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как производную по времени:
За единицу скорости принимают 1м/с. Иногда скорость измеряют в км/ч,
Слайд 55д) Ускорение точки
Векторная величина, характеризующая быстроту изменения скорости по величине
и направлению, называется ускорением точки.
Скорость точки при перемещении из точки
M1 в точку М2 меняется по величине и направлению. Среднее значение ускорения за этот промежуток времени (см. рис. 9.4.)Рис.9.4. Ускорение точки.
Слайд 56При рассмотрении бесконечно малого промежутка времени среднее ускорение превратится в
ускорение в данный момент:
Обычно для удобства рассматривают две взаимно перпендикулярные
составляющие ускорения: нормальное и касательное (рис. 9.5).Нормальное ускорение αn характеризует изменение скорости по направлению и определяется как →
где r — радиус кривизны траектории в данный момент времени.
Слайд 57Касательное ускорение αt характеризует изменение скорости по величине и всегда
направлено по касательной к траектории; при ускорении его направление совпадает
с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости.Формула для определения касательного ускорения имеет вид:
Слайд 58Значение полного ускорения определяется как: (см. рис. 9.6).
Рис.9.6.
Определение полного ускорения
