Функция y=ax2+bx+c, её свойства и график

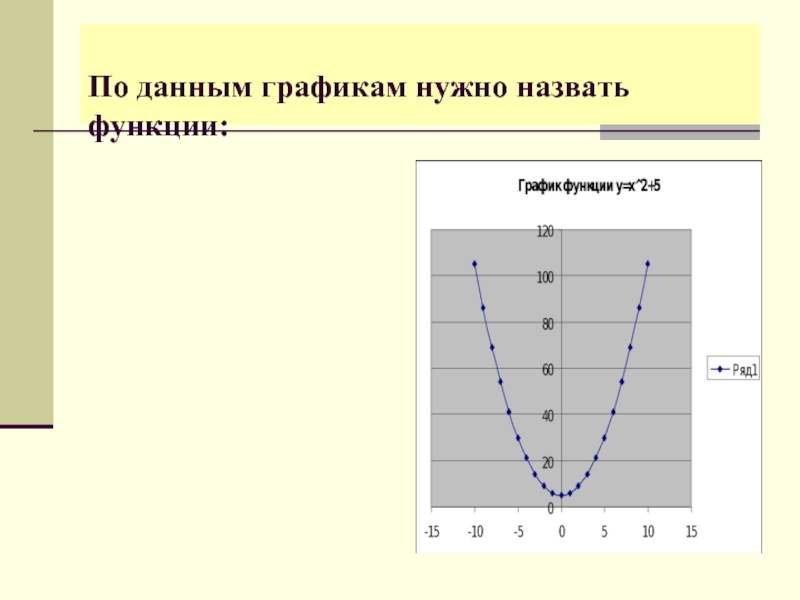
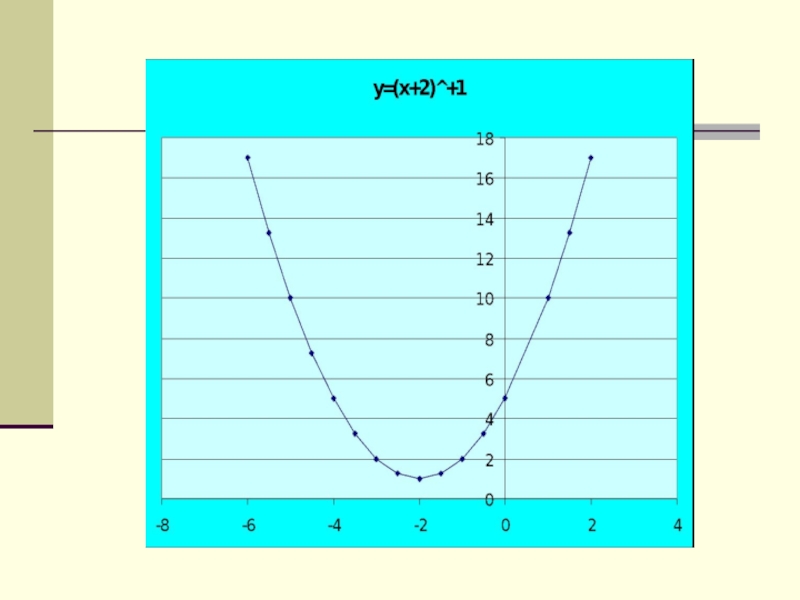
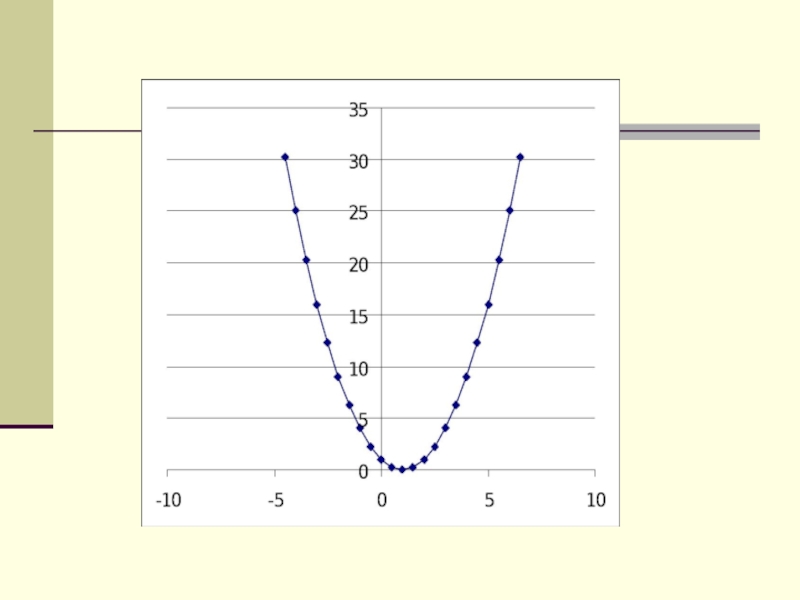
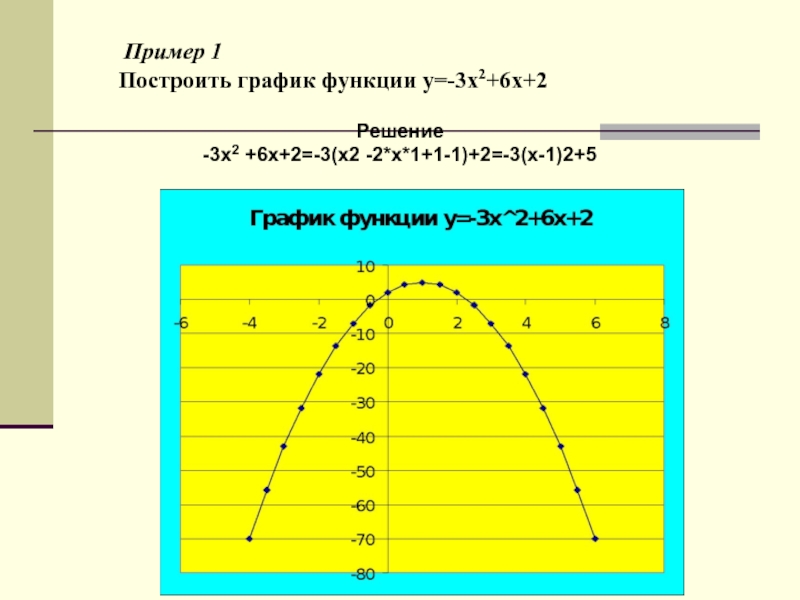
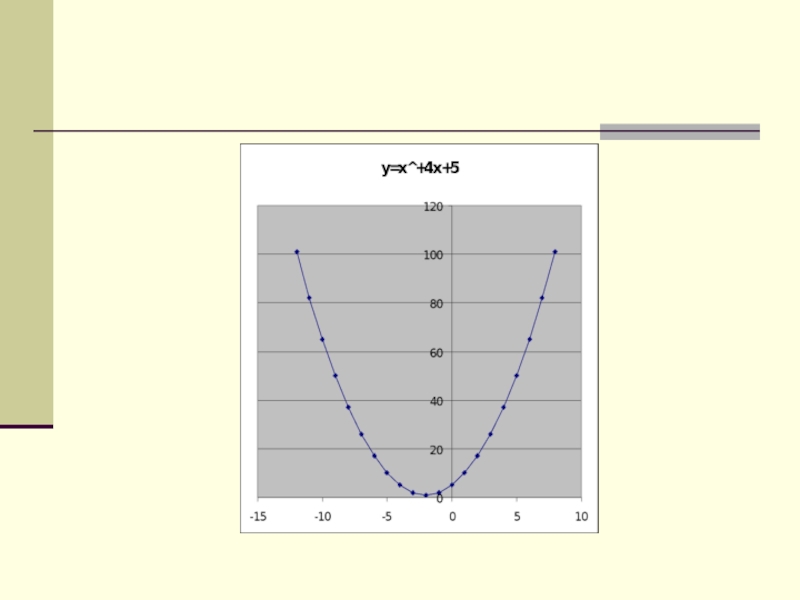
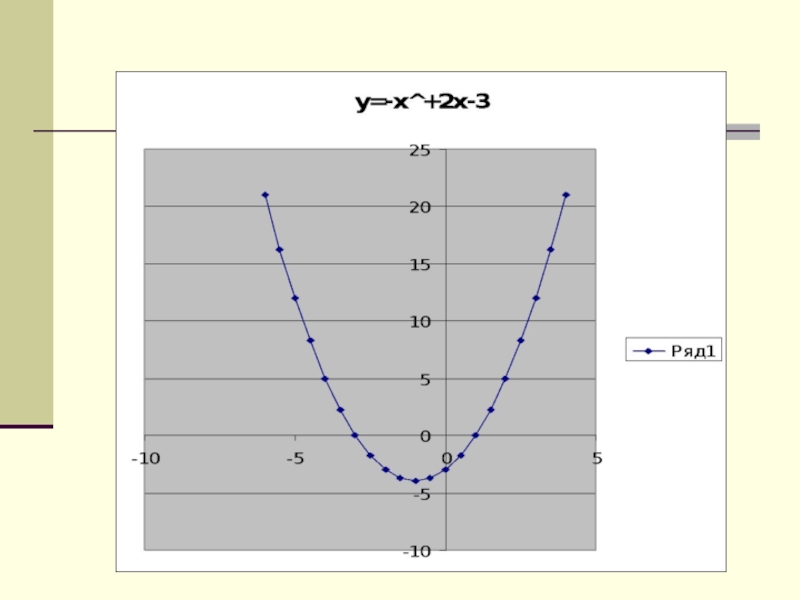
- ввести алгоритм построения графика функции y=ax2+bx+c;

- рассмотреть свойства данной функции;
- формировать умение строить график данной функции.
«Весь анализ бесконечных вращается
вокруг переменных величин и их функций»
Л.Эйлер

На координатной плоскости с

помощью шаблонов построить график данных функций.
В. 1. В.2.
1) y = 2 x2–1 1) y = 0,5 ( x + 2 )2
2) y =-2(x+3)2 -2 2) y = - (x - 3)2 + 6
3) y =1/2(x-3)2 3) y = 2 x 2 - 3

а) а 2 -2а * +в 2 = (а -

*)2
б) 4u2 – 8u v + *2 =(2u-*)2
в) x2 +6x + *2 = (x + *)2
г) 9 – 2y * +*2 = (3 - *)2
4. Выделить полный квадрат из трёхчлена:
а) x2 – 8x +14 =
б) x2 + 6x + 10 =

2

является прямая x = - L, т. е. x =

-.b\2a
Вывод:
Осью параболы y = ax2 + bx + c служит прямая x = - b\2a; абсцисса x0 вершины параболы y = ax2 + bx + c вычисляется по формуле x0 = -d\2a .
Формулу для ординаты вершин параболы запоминать не нужно ( y0 = ) y0 = f(x0) !

Куда направлены ветви параболы.
2) Найти уравнение оси параболы.
3) Найти координаты

вершины параболы.
Например:
1) у = 4 x 2 + 8x - 1;
2) y = - 3 x2 - 6x + 2;
3) y = - x 2 + x - 1;
4) y = 5 x 2 - 10x + 2.

у = 7 x 2 – 3 x 2 -

2; в) у = 8 x 2 - 2x;

б) у = 0,5 x 2 + 1; г) у=0,4x+1\7-3\10x2;

2. Запишите уравнение прямой, которая является осью симметрии параболы:
а) у=2x2-x+1 ;
в) у=7x2+12x+4;
б) у=-5x2+2x-2 ; г) у=6x2+9x-3;

3. Найти координаты вершины параболы:

а) у=-4x2+8x-1; б) у= -x2+x-1; в) у=-3x2-6x+2;

У = x2 + 4х - 1

3) У = х2

- 4х