Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интерактивный плакат "Математические функции"
Содержание
- 1. Интерактивный плакат "Математические функции"
- 2. Математические функции Линейная функция Преобразование графика функции
- 3. Линейная функция1.Линейная функция и её свойства.
- 4. Линейная функция2.Постоянная функция.Если k=0, то линейная функция
- 5. Линейная функция3.Прямая пропорциональность. Если b=0,
- 6. Линейная функция4.Взаимное расположении графиков двух линейных функций
- 7. Степенная функция с целым показателем
- 8. Степенная функция с целым показателем Квадратичная
- 9. Степенная функция с целым показателем Кубическая
- 10. Степенная функция с целым показателем Обратная
- 11. Тригонометрические функцииОПРЕДЕЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙРассмотрим на координатной плоскости
- 12. y = sin xD(f)= R;E(f)=[-1;1]ограничена сверху
- 13. y = сos xD(f)= R;E(f)=[-1;1]ограничена сверху
- 14. y = tg xD(f)= R кроме
- 15. y = ctg xD(f)= R кроме
- 16. Преобразование графика функции
- 17. Преобразование графика функции
- 18. Проверка Здесь вы можете проверить усвоенный материал
- 19. Проверка Найдите область определения и область значения
- 20. Хотите проверить себя через INTERNEThttp://uztest.ru/plugins/lessons/pazl/moe/tests/fun1/erkennen.html - тест
- 21. Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №23Автор:
- 22. Мы должны знать – мы будем знать!Д. Гильберт
- 23. Задание 1. Установите соответствие1)2)3)4)5)6)Ответ:Ответ:Ответ:Ответ:Ответ:Ответ:проверка
- 24. Задание 2. Используя графики функций на рисунках
- 25. Задание 3. Используя графики функций на рисунках
- 26. Задание 4. Используя графики функций на рисунках
- 27. Задание 5. По графику функции определите промежутки
- 28. Задание 6. По рисункам 1 – 12
- 29. Задание 6. По рисункам 1 – 12
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
ИНТЕРАКТИВНЫЙ ПЛАКАТ «ФУНКЦИИ»
Головина Наталья Николаевна
Учитель математики
МОУ «Бессоновская
СОШ
Слайд 2Математические функции
Линейная функция
Преобразование графика функции
Тригонометрические функции
Степенная функция с целым показателем
Задания для проверки
Давайте отдохнем
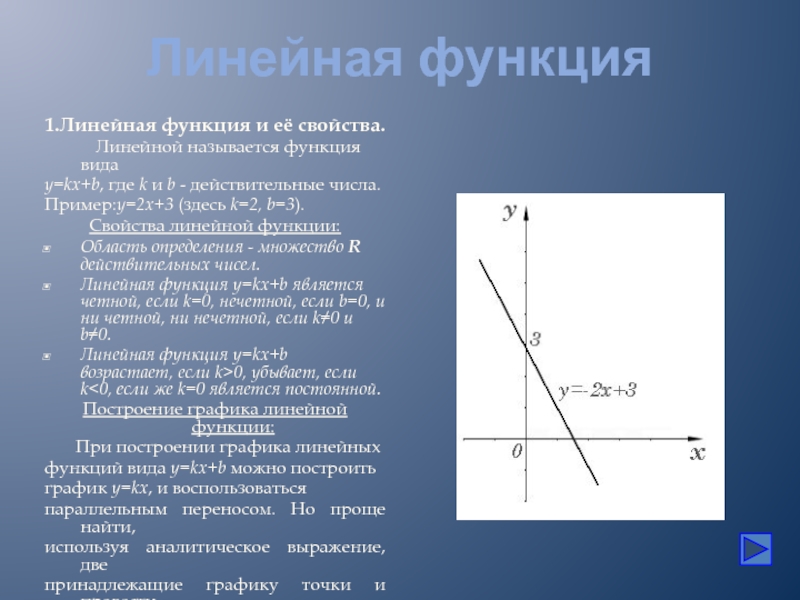
Слайд 3Линейная функция
1.Линейная функция и её свойства.
Линейной называется функция вида
y=kx+b, где k и
b - действительные числа. Пример:y=2x+3 (здесь k=2, b=3).
Свойства линейной функции:
Область определения - множество R действительных чисел.
Линейная функция y=kx+b является четной, если k=0, нечетной, если b=0, и ни четной, ни нечетной, если k≠0 и b≠0.
Линейная функция y=kx+b возрастает, если k>0, убывает, если k<0, если же k=0 является постоянной.
Построение графика линейной функции:
При построении графика линейных
функций вида y=kx+b можно построить
график y=kx, и воспользоваться
параллельным переносом. Но проще найти,
используя аналитическое выражение, две
принадлежащие графику точки и провести
через них прямую.
Слайд 4Линейная функция
2.Постоянная функция.
Если k=0, то линейная функция является
постоянной, т.к.
y=b. Получается, что все точки
графика данной зависимости будут иметь
одинаковую ординату y, которая будет равна b.
Свойства постоянной функции y=b.
D(f)= R;
E(f)= b;
ограничена сверху и снизу на всей области своего существования;
не принимает, ни наибольшего, ни наименьшего значения;
не периодическая;
четная;
постоянна на всей области своего существования;
пересекает ось ординат в точке (0;b)
графиком данной функции является прямая, параллельная оси Ox и пересекающая ось Oy в точке (0;b).
Слайд 5Линейная функция
3.Прямая пропорциональность.
Если b=0, то линейная функция
y=kx+b имеет вид
y=kx и называется прямой пропорциональностью; в этом
случае коэффициент k называется коэффициентом
пропорциональности.Пример:y=2x
Свойства прямой пропорциональности y=kx.
D(f)= R;
E(f)= R;
не ограничена ни снизу не сверху;
не принимает, ни наибольшего, ни наименьшего значения;
не периодическая;
нечетная;
возрастает на R при k>0 и убывает при k<0;
точка (0;0) - единственная точка пересечения с осями координат;
графиком данной функции является прямая, проходящая через начало координат.
Построение графика прямой пропорциональности:
При построении графиков линейных зависимостей
вида y=kx достаточно найти одну точку, принадлежащую
графику и отличную от нуля, и провести прямую через эту
точку и начало координат.
Слайд 6Линейная функция
4.Взаимное расположении графиков двух
линейных функций y=k1x+b1 и y=k2x+b2
если k1≠k2, b1≠b2, то прямые, служащие графиками данных функций пересекаются;
если
k1=k2, b1=b2, то прямые совпадают;если k1=k2, b1≠b2, то прямые параллельны;
если k1≠k2, b1=b2, то прямые пересекаются в точке, принадлежащей оси Oy.
Слайд 7Степенная функция с целым показателем
Здесь мы
рассмотрим степенную функцию с произвольным целым показателем, т.е.
зависимость вида
y=xm, где m - целое число. m=0 ,получаем функцию вида y=1, x≠0 - постоянная функция с проколом в точке (0;1)
m=1, получаем y=x – линейная функция, графиком является прямая проходящая через начало координат и являющаяся биссектрисой первого и третьего координатных углов
m=2, квадратичная функция y=x2
m=3, кубическая функция y=x3
m=-1, обратная пропорциональность y=1/x
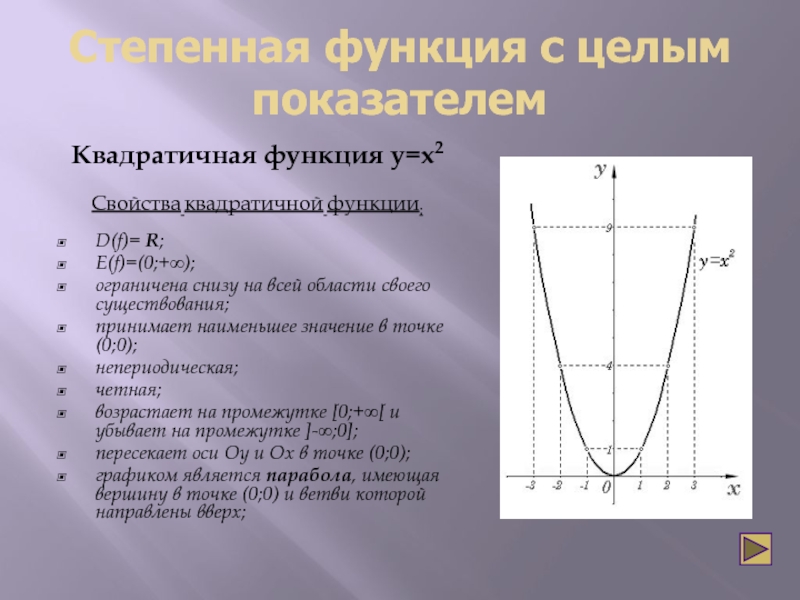
Слайд 8Степенная функция с целым показателем
Квадратичная функция y=x2
Свойства квадратичной функции:
D(f)=
R;
E(f)=(0;+∞);
ограничена снизу на всей области своего существования;
принимает наименьшее значение в
точке (0;0);непериодическая;
четная;
возрастает на промежутке [0;+∞[ и убывает на промежутке ]-∞;0];
пересекает оси Oy и Ox в точке (0;0);
графиком является парабола, имеющая вершину в точке (0;0) и ветви которой направлены вверх;
Слайд 9Степенная функция с целым показателем
Кубическая функция y=x3
Свойства кубической функции:
D(f)=
R;
E(f)= R;
не ограничена ни снизу, ни сверху на всей области
своего существования;не принимает ни наибольших, ни наименьших значений;
непериодическая;
нечетная;
возрастает на R;
пересекает оси Oy и Ox в точке (0;0);
графиком является кубическая парабола, пересекающая начало координат;
Слайд 10Степенная функция с целым показателем
Обратная пропорциональность y =
Свойства обратной
пропорциональности:
D(f)= (-∞;0)∪ (0;+∞);
E(f)= (-∞;0)∪ (0;+∞);
не ограничена ни снизу, ни сверху
на всей области своего существования;не принимает ни наибольших, ни наименьших значений;
непериодическая;
нечетная;
убывает на всей области своего существования;
не имеет пересечений с осями координат;
имеет горизонтальную и вертикальную ассимптоты, которыми являются оси координат;
графиком является гипербола;
Слайд 11Тригонометрические функции
ОПРЕДЕЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Рассмотрим на координатной плоскости окружность
радиуса R
= 1с центром O в начале координат.
Координатные оси делят окружность
на четыре дуги, которые называют четвертями. Рассмотрим произвольный
угол . Точка M(x;y) лежит на единичной окружности,
считаем, что точка M результат поворота точки A(1;0) на
угол . На оси OX находятся значения cos угла поворота, а
на оси OY, соответственно, находятся значения sin
углов поворота. На дополнительных осях ctg и
tg параллельных осям OX и OY, соответственно,
находятся значения ctg и tg угла поворота.
Тригонометрические функции определяются следующими равенствами:
синус: sin =y, т.е. ордината точки M;
косинус: cos =x, т.е. абсцисса точки M;
тангенс: tg =x : y, т. е. отношение ординаты к абсциссе точки M;
котангенс: ctg =y : x, т. е. отношение абсциссы к ординате точки M.
Замечание. Значение tg угла поворота не существует для углов 2 + n n Z. Значение ctg угла поворота не существует для углов n n Z.
Слайд 12 y = sin x
D(f)= R;
E(f)=[-1;1]
ограничена сверху и снизу на
всей области своего существования;
при x=π/2+2πn, n∈Z принимает наибольшее значение y=1,
а при x=-π/2+2πn, n∈Z принимает наименьшее значение y=-1;периодическая с основным периодом 2π;
нечетная;
возрастает на отрезке [0+2πn;π/2+2πn], n∈Z и убывает на отрезке [π/2+2πn;π+2πn], n∈Z;
пересекает ось абсцисс в точках (π+πn;0), n∈Z и ось ординат в точке (0;0);
графиком является синусоида.
Слайд 13 y = сos x
D(f)= R;
E(f)=[-1;1]
ограничена сверху и снизу на
всей области своего существования;
при x=0+2πn, n∈Z принимает наибольшее значение y=1,
а при x=π+2πn принимает наименьшее значение y=-1;периодическая с основным периодом 2π;
четная;
возрастает
на отрезке[-π+2πn;0+2πn], n∈Z и убывает на отрезке [0+2πn;π+2πn], n∈Z;
пересекает ось абсцисс в точках (π/2+πn;0), n∈Z и ось ординат в точке (0;1);
графиком является косинусоида.
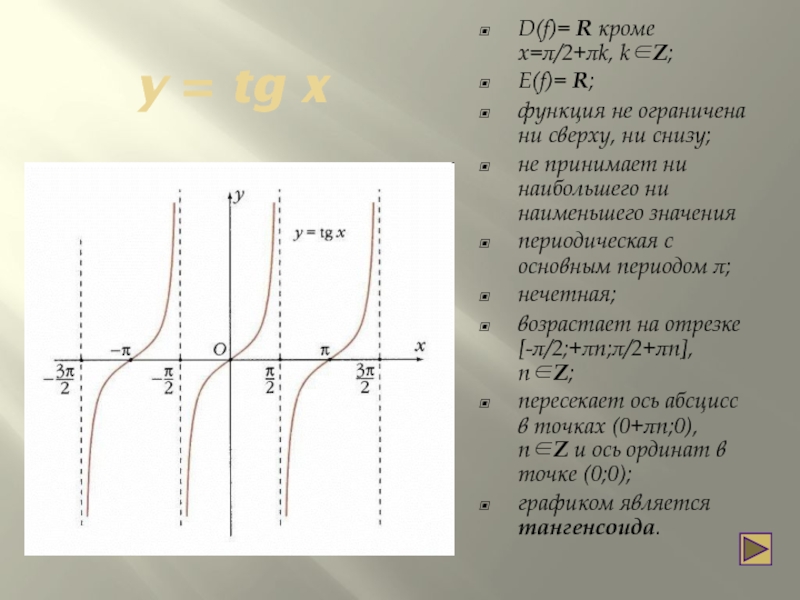
Слайд 14 y = tg x
D(f)= R кроме x=π/2+πk, k∈Z;
E(f)= R;
функция
не ограничена ни сверху, ни снизу;
не принимает ни наибольшего ни
наименьшего значенияпериодическая с основным периодом π;
нечетная;
возрастает на отрезке [-π/2;+πn;π/2+πn], n∈Z;
пересекает ось абсцисс в точках (0+πn;0), n∈Z и ось ординат в точке (0;0);
графиком является тангенсоида.
Слайд 15 y = ctg x
D(f)= R кроме x=π+πk, k∈Z;
E(f)= R;
функция
не ограничена ни сверху, ни снизу;
не принимает ни наибольшего ни
наименьшего значенияпериодическая с основным периодом π;
нечетная;
убывает на отрезке [0+πn;π+πn], n∈Z;
пересекает ось абсцисс в точках (π/2+πn;0), n∈Z, не имеет пересечений с осью ординат;
графиком является котангенсоида.
Слайд 18Проверка
Здесь вы можете проверить усвоенный материал удобным для вас
способом:
Ответить на вопросы прямо сейчас пройдя по ссылке, при этом
сможете сразу проверить свои ответы.Хотите более сложный уровень, нажмите ОК и выбирайте интересующий вас вопрос.
Подключить INTERNET и пройти независимое тестирование.
Слайд 19Проверка
Найдите область определения и область значения функции, заданной графически.
Найдите
область определения функции, заданной аналитически.
Установите вид функции по её графику.
Если вы хотите ответить на эти вопросы нажмите ОК
Определите вид тригонометрической функции по её графику.
Если вы хотите ответить на эти вопросы нажмите ОК
Установите соответствие между видом функции и его графиком.
Постройте график заданной функции.
Если вы хотите ответить на эти вопросы нажмите ОК
Назад к видам проверки
Слайд 20Хотите проверить себя через INTERNET
http://uztest.ru/plugins/lessons/pazl/moe/tests/fun1/erkennen.html - тест на соответствие формул
и графиков;
http://uztest.ru/simulator - тренажер на знание различных функций и их
свойств;Назад к видам проверки
Слайд 21Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа №23
Автор: Лариса Анатольевна Зубкова,
учитель математики и информатики
Рыбинск, 2008
Свойства функций
(тест с проверкой)
Слайд 24Задание 2.
Используя графики функций на рисунках 1 - 9,
укажите области определения этих функций
1) (-∞; + ∞)
2) (-∞; -
1]3) (-∞; 0]
4) (-∞; 0) ∪ (0; + ∞)
5) [-2; 4]
6) [0; + ∞)
8) [-2; + ∞)
7) [-4; 4]
9) (-∞; 3)
1) (-∞; + ∞)
1) (-∞; + ∞)
1) (-∞; + ∞)
1) (-∞; + ∞)
4) (-∞; 0) ∪ (0; + ∞)
6) [0; + ∞)
3) (-∞; 0]
7) [-4; 4]
проверка
Слайд 25Задание 3.
Используя графики функций на рисунках 1 - 9,
укажите область значений этих функций
1) (-∞; + ∞)
2) (-∞; -
1]3) (-∞; 0]
4) (-∞; 0) ∪ (0; + ∞)
5) [-2; 4]
6) [0; + ∞)
8) [-2; + ∞)
7) [-4; 4]
9) (-∞; 3)
1) (-∞; + ∞)
8) [-2; + ∞)
9) (-∞; 3)
2) (-∞; - 1]
6) [0; + ∞)
4) (-∞; 0) ∪ (0; + ∞)
6) [0; + ∞)
5) [-2; 4]
проверка
Слайд 26Задание 4. Используя графики функций на рисунках 1 – 9
определите, какие из функций:
1) Ограничены сверху
2) Ограничены снизу
3) Ограничены
4) Не
ограниченыОтвет:
Ответ:
Ответ:
Ответ:
2)
снизу
ограничена
сверху
не ограничена
снизу
не ограничена
сверху
ограничена
снизу
проверка
Слайд 27Задание 5. По графику функции определите промежутки монотонности функций
Функция возрастает
Ответ:
Ответ:
Ответ:
Функция
убывает
Ответ:
Функция возрастает
Функция убывает
[- 3; - 2] ∪ [2; 3]
[3; 5]
[-
5; - 3][- 3; 2] ∪ [3; 4]
проверка
Слайд 28Задание 6. По рисункам 1 – 12 укажите наибольшие и
наименьшие значения функций
Унаим = - 2
Унаим = 0
Унаим =
0Унаиб = 3
Нет Унаиб и Унаим
Нет Унаиб и Унаим
проверка
Слайд 29Задание 6. По рисункам 1 – 12 укажите наибольшие и
наименьшие значения функций
Унаиб = - 1
Унаиб = 2 ;
Унаим = - 2Унаиб = 2 ; Унаим = - 2
Унаиб = 2 ; Унаим = - 2
Унаиб = 2 ; Унаим = - 2,5
Унаиб = 3 ; Унаим = - 3
проверка









![Интерактивный плакат y = sin xD(f)= R;E(f)=[-1;1]ограничена сверху и снизу на всей области своего существования;при x=π/2+2πn, n∈Z принимает](/img/thumbs/cef70822b60234a629635ad7fcfddb5c-800x.jpg)
![Интерактивный плакат y = сos xD(f)= R;E(f)=[-1;1]ограничена сверху и снизу на всей области своего существования;при x=0+2πn, n∈Z принимает](/img/thumbs/99024026ae65c0be24d26d686b51bb60-800x.jpg)












![Интерактивный плакат Задание 5. По графику функции определите промежутки монотонности функцийФункция возрастаетОтвет:Ответ:Ответ:Функция убываетОтвет:Функция возрастаетФункция убывает[- 3; - 2] ∪](/img/thumbs/bb641c73ec7f71ea510e967a3d9e36ec-800x.jpg)





















