квадратного уравнения?
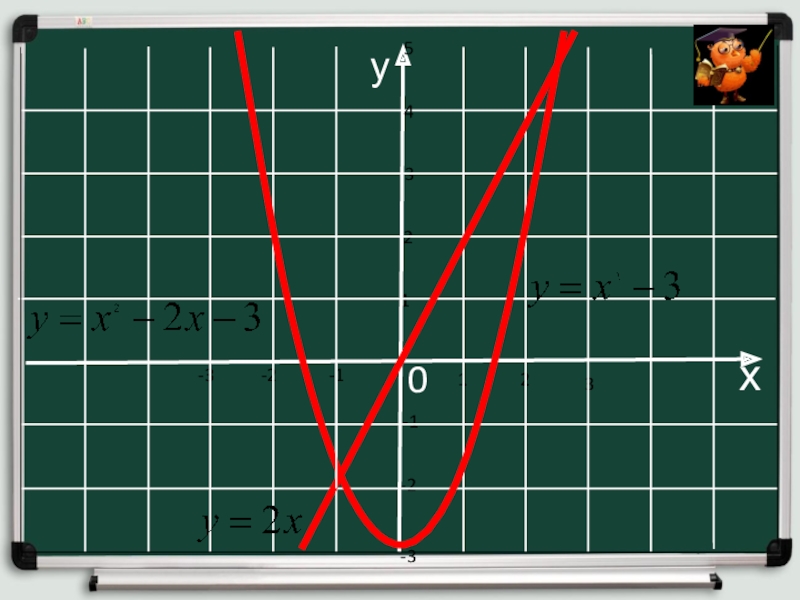
Сколько корней имеет квадратное уравнение, если D > 0;
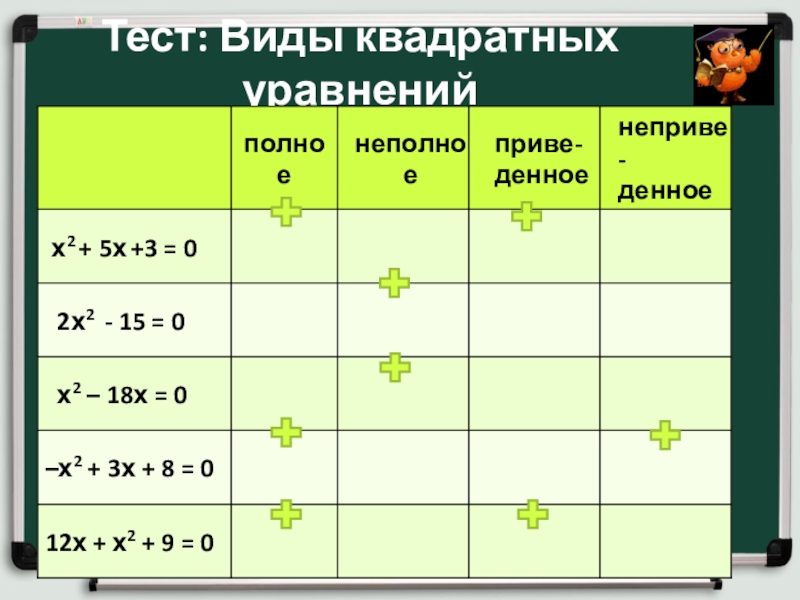
D < 0; D = 0?Как называется квадратное уравнение, у которого первый коэффициент – равен 1?
Что значит решить уравнение?