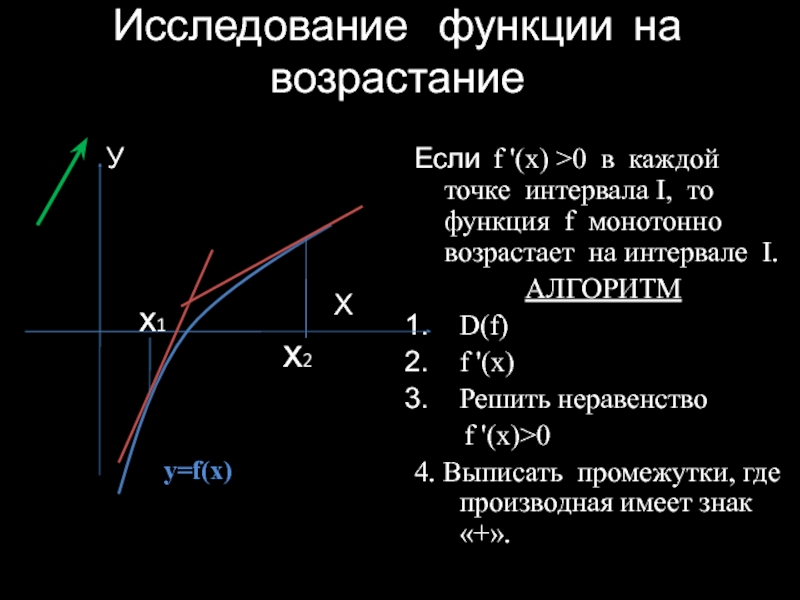
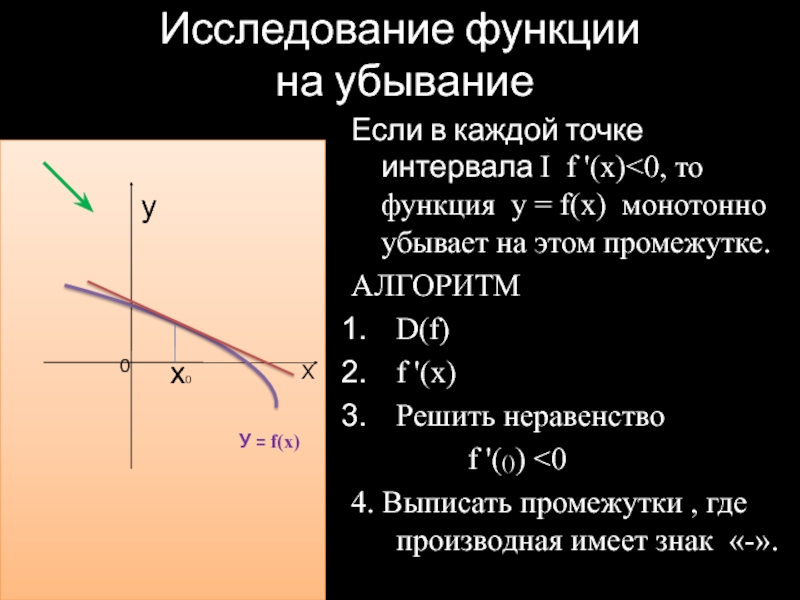
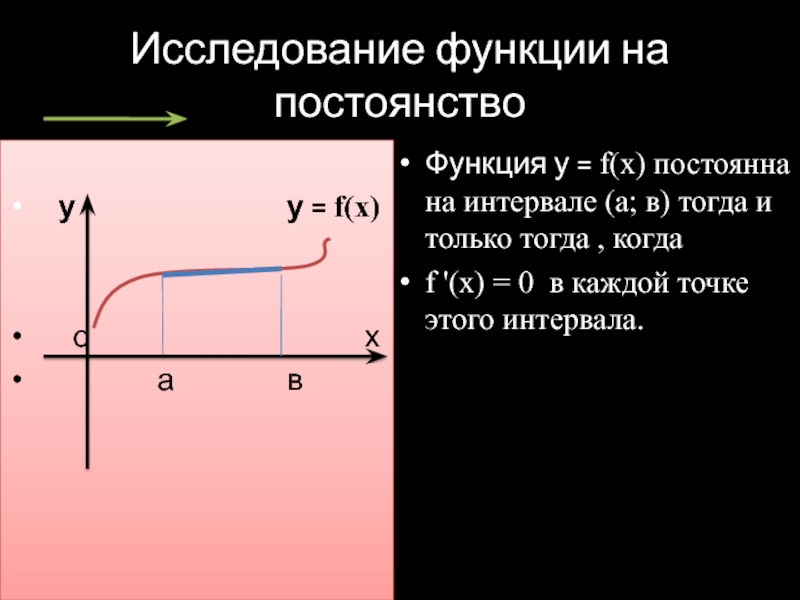
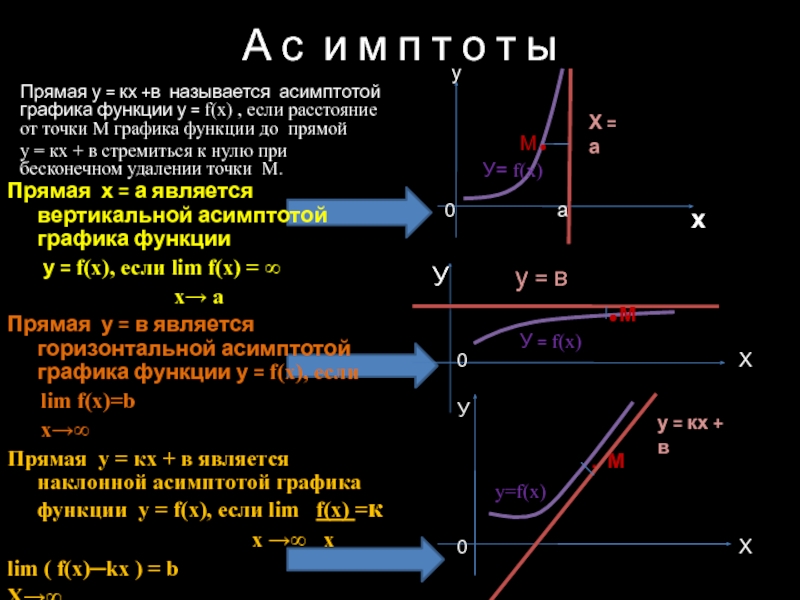
Нахождение промежутков убывания функции.
3. Нахождение промежутков постоянства функции.
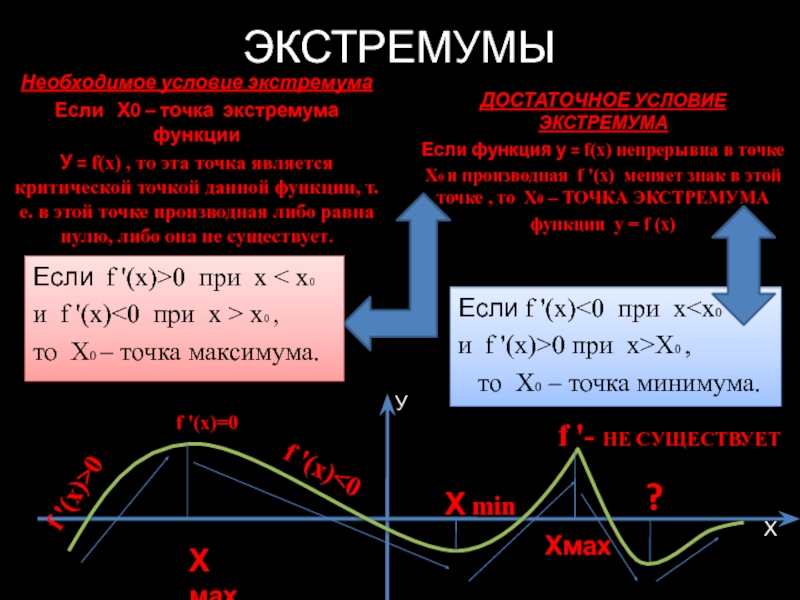
4. Нахождение экстремумов.
5.
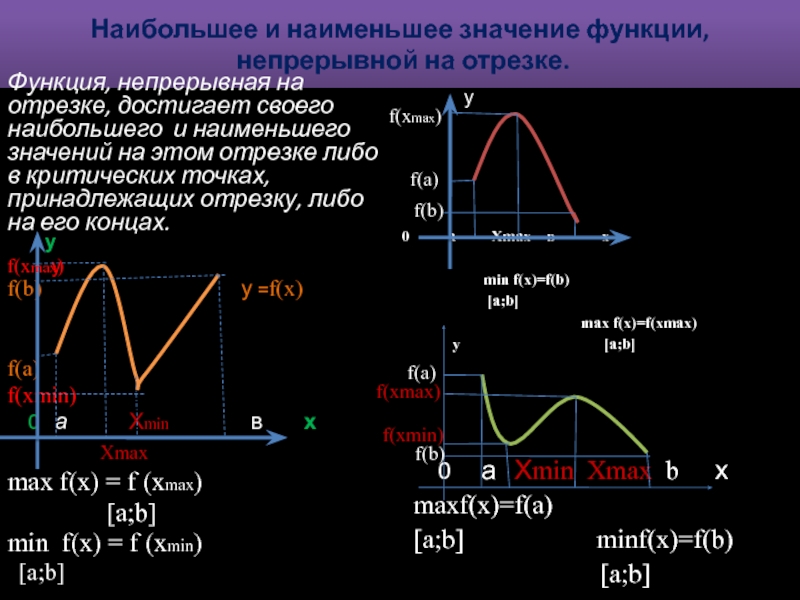
Решение уравнений.6.Нахождение наибольшего и наименьшего значения функции, непрерывной на отрезке.