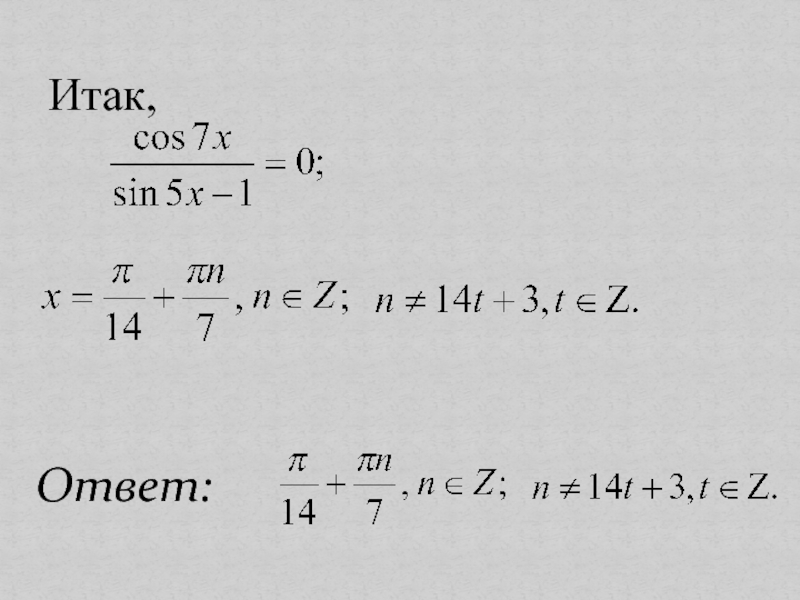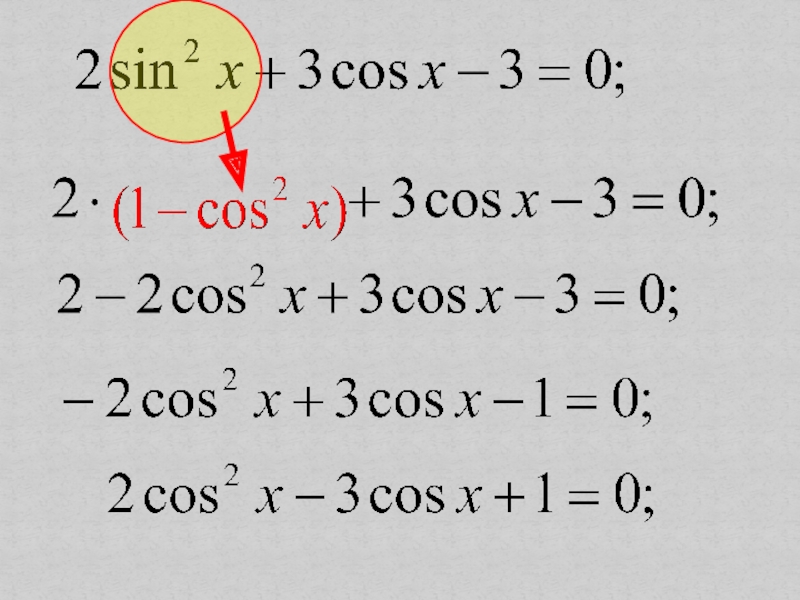Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы отбора корней в тригонометрических уравнениях
Содержание
- 1. Способы отбора корней в тригонометрических уравнениях
- 2. Способы отбора корней в тригонометрических уравнениях АрифметическийФункционально-графическийАлгебраическийГеометрический
- 3. Арифметический способ перебор значений целочисленного параметра и вычисление корней.
- 4. Слайд 4
- 5. Слайд 5
- 6. Алгебраический способа) решение неравенства относительно неизвестного целочисленного
- 7. Слайд 7
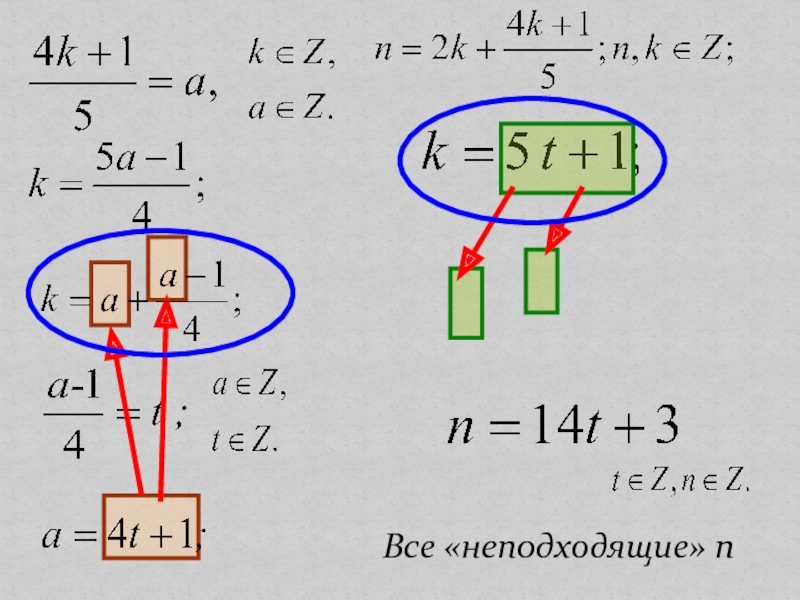
- 8. Найдём все «неподходящие» n.
- 9. Все «неподходящие» n
- 10. Итак,Ответ:
- 11. Решить уравнение
- 12. Слайд 12
- 13. n=2
- 14. а) изображение корней на тригонометрической окружности с
- 15. Слайд 15
- 16. Решить уравнение
- 17. общий множительобщий множитель
- 18. Слайд 18
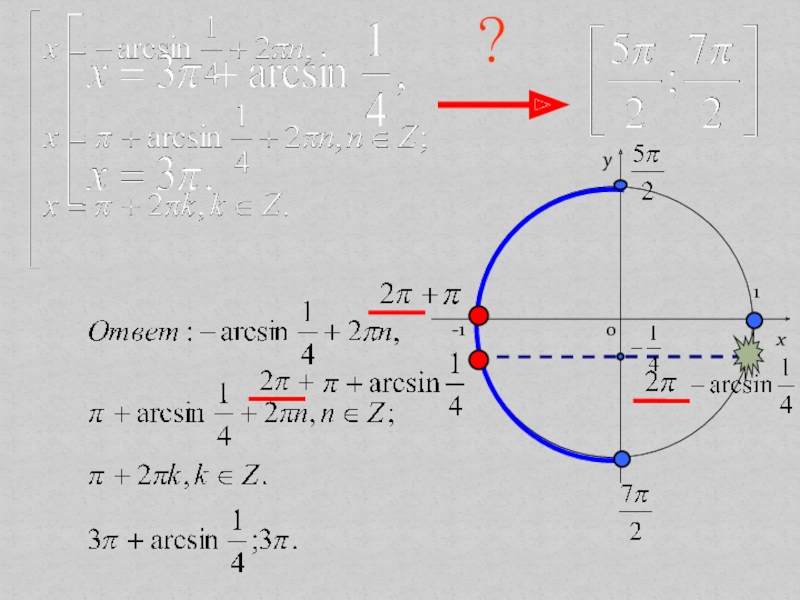
- 19. ?
- 20. Решить уравнениеУкажите корни, принадлежащие отрезку.
- 21. Разделим на cos2x; cos2x≠0.
- 22. 1-1,5?
- 23. Отбор корней на координатной прямой.х0
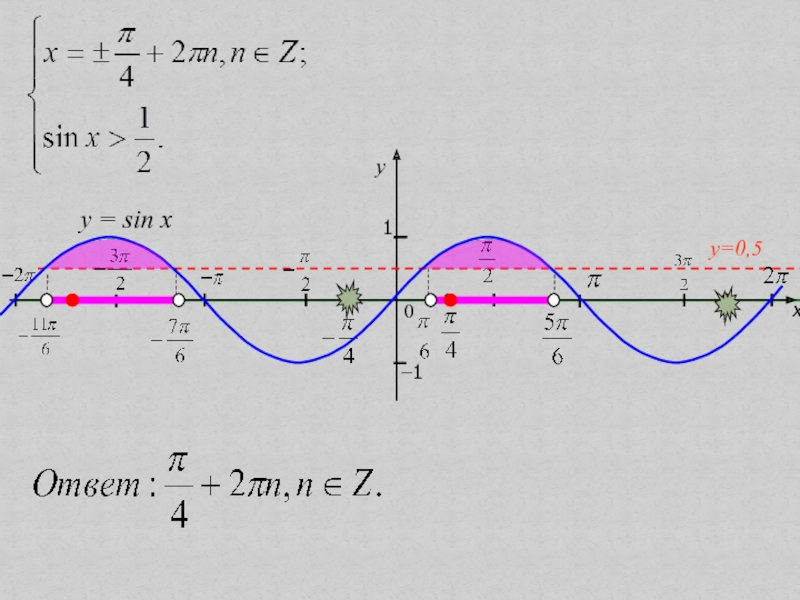
- 24. Функционально-графическийспособвыбор корней с использованием графика простейшей тригонометрической функции.
- 25. Решите уравнение
- 26. xy10−1y=0,5y = sin x
- 27. Дано уравнение:а) Решите уравнение. б) Укажите корни
- 28. Найдём корни уравнения, принадлежащие отрезкуИтак, первый
- 29. Решаем неравенство:Для полученного неравенства целого числа k не существует.Следующий корень:Решаем неравенство:
- 30. Так как число k целое, то k = 1.Находим корень принадлежащий интервалу:Ответ:
- 31. http://alexlarin.net/ege/2012/C12012.pdf2. ЕГЭ-2012.Математика: типовые экзаменационные варианты: 30 вариантов/
- 32. Скачать презентанцию
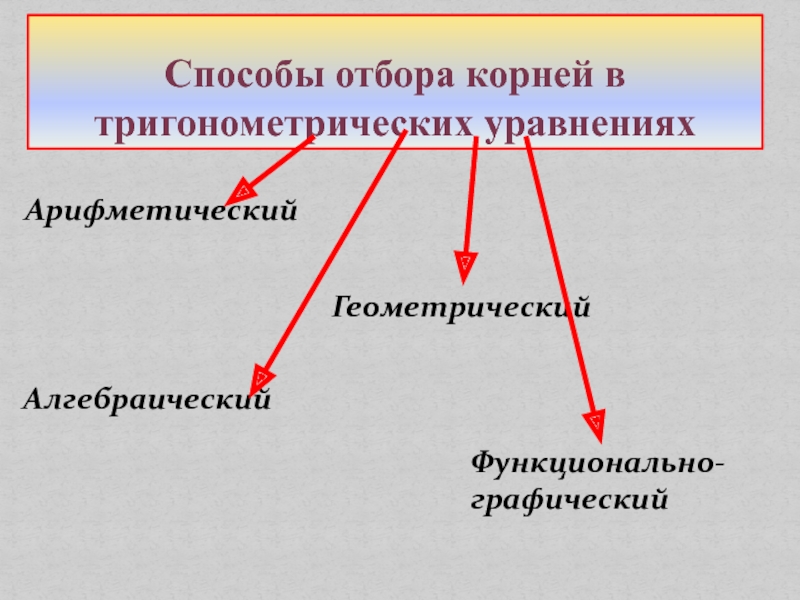
Способы отбора корней в тригонометрических уравнениях АрифметическийФункционально-графическийАлгебраическийГеометрический
Слайды и текст этой презентации
Слайд 2Способы отбора корней в тригонометрических уравнениях
Арифметический
Функционально-графический
Алгебраический
Геометрический
Слайд 6Алгебраический способ
а) решение неравенства относительно неизвестного целочисленного параметра и вычисление
корней;
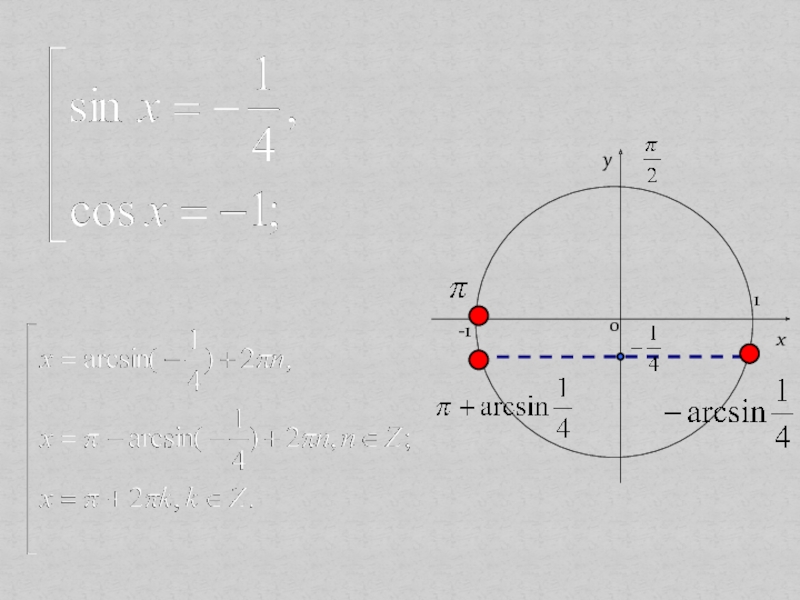
Слайд 14а) изображение корней на тригонометрической окружности с последующим их отбором
на заданном промежутке;
б) изображение корней на координатной прямой с последующим
отбором с учетом имеющихся ограничений.Геометрический способ:
Слайд 24Функционально-графический
способ
выбор корней с использованием графика простейшей тригонометрической функции.
Слайд 27Дано уравнение:
а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие отрезку
Решение:
Тогда
cos x = 0 или sin x = 0,5
Слайд 28 Найдём корни уравнения, принадлежащие отрезку
Итак, первый корень:
Решаем неравенство:
Так число
k целое, то k1 = 2 k2 = 3
Находим корни, принадлежащие интервалу:
Следующий
корень:
Слайд 29Решаем неравенство:
Для полученного неравенства целого числа k не существует.
Следующий корень:
Решаем
неравенство:
Слайд 31http://alexlarin.net/ege/2012/C12012.pdf
2. ЕГЭ-2012.Математика: типовые экзаменационные варианты: 30 вариантов/ под ред. А.Л.
Семёнова, И.В.Ященко.-М.: Национальное образование, 2011. (ЕГЭ -2012. ФИПИ – школе).
В
презентации использовались ресурсы:
