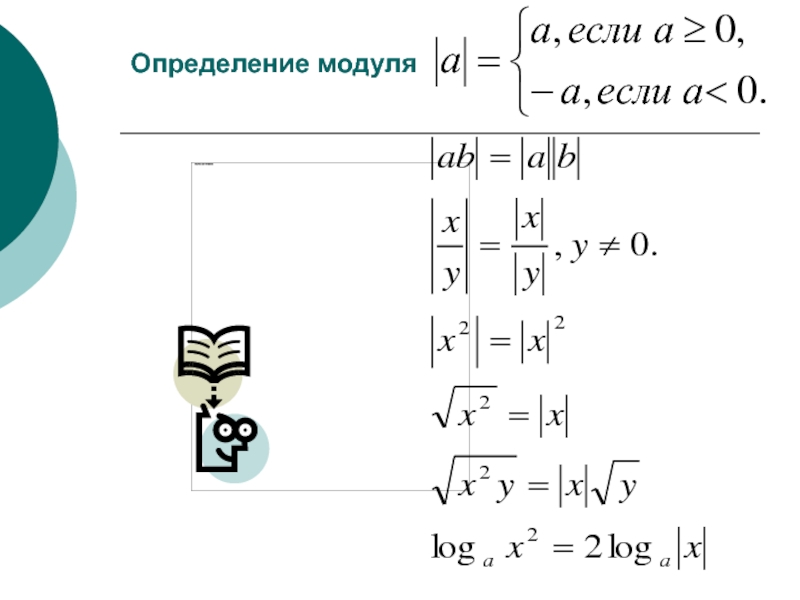
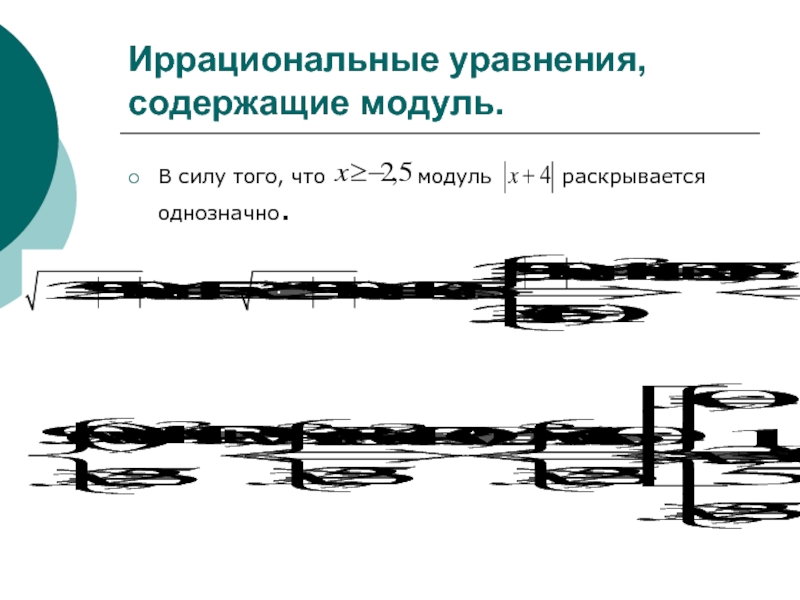
и его свойствах, умения решать различные уравнения , содержащие модуль.
Учитель МОУ СОШ №6 г.Маркса
Мартышова Л. И.
Модуль
Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль.
Учитель МОУ СОШ №6 г.Маркса
Мартышова Л. И.
Модуль
Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль.
Учитель МОУ СОШ №6 г.Маркса
Мартышова Л. И.
Модуль
Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль.
Учитель МОУ СОШ №6 г.Маркса
Мартышова Л. И.
Модуль