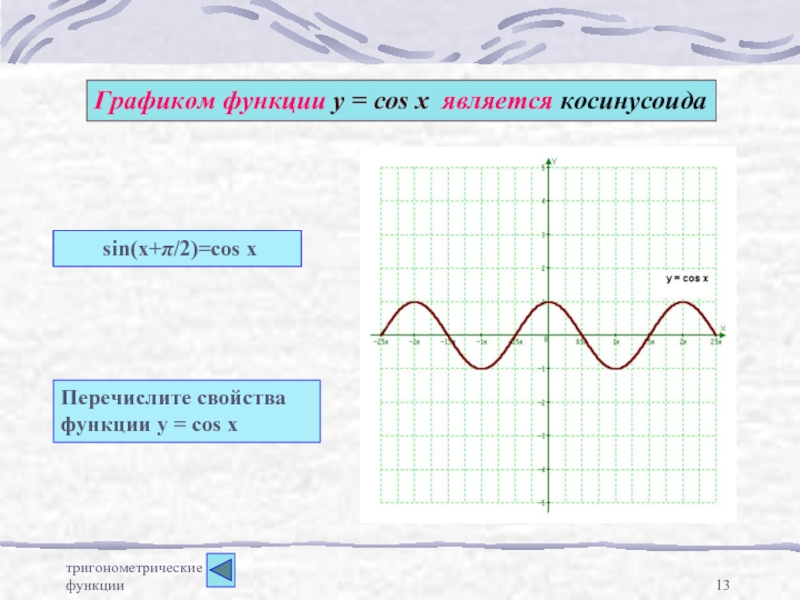
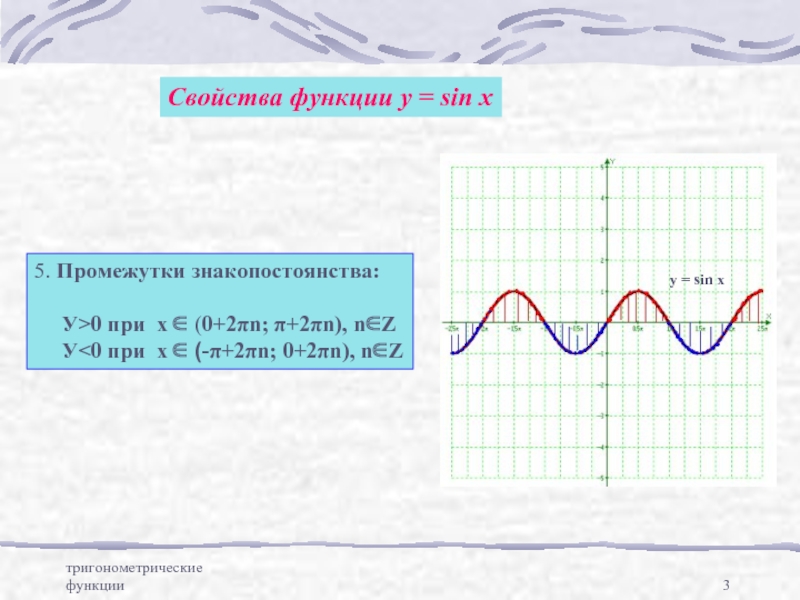
у = sin x, ее свойства
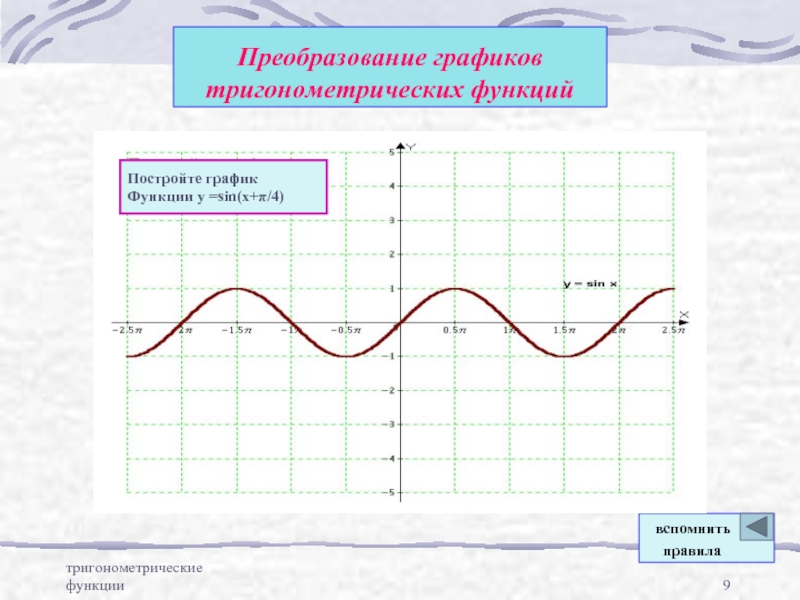
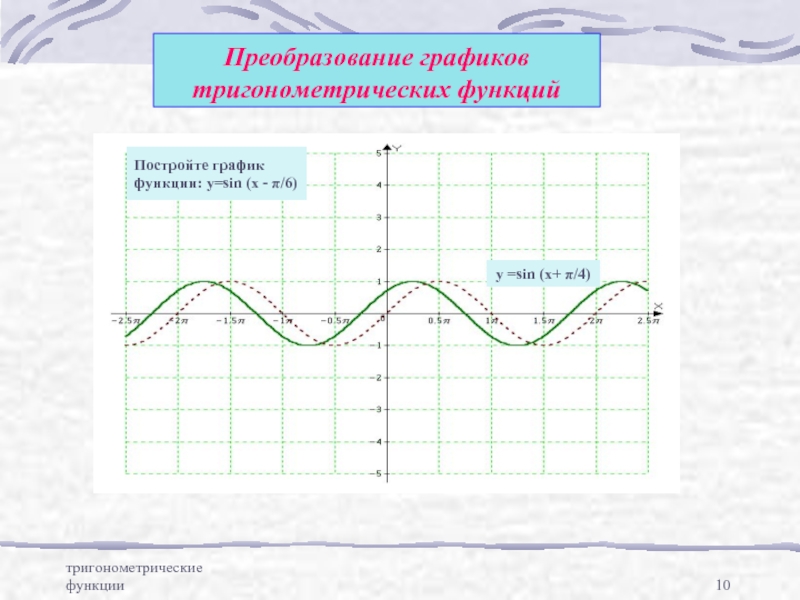
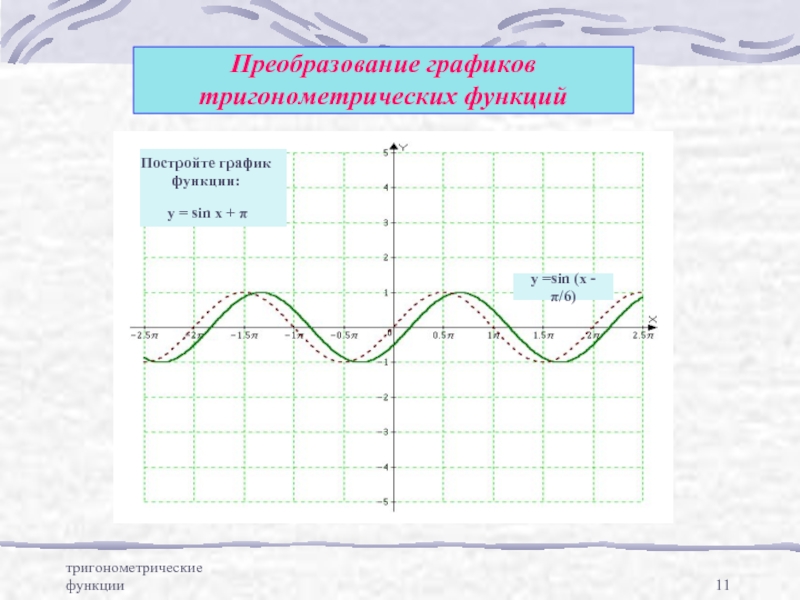
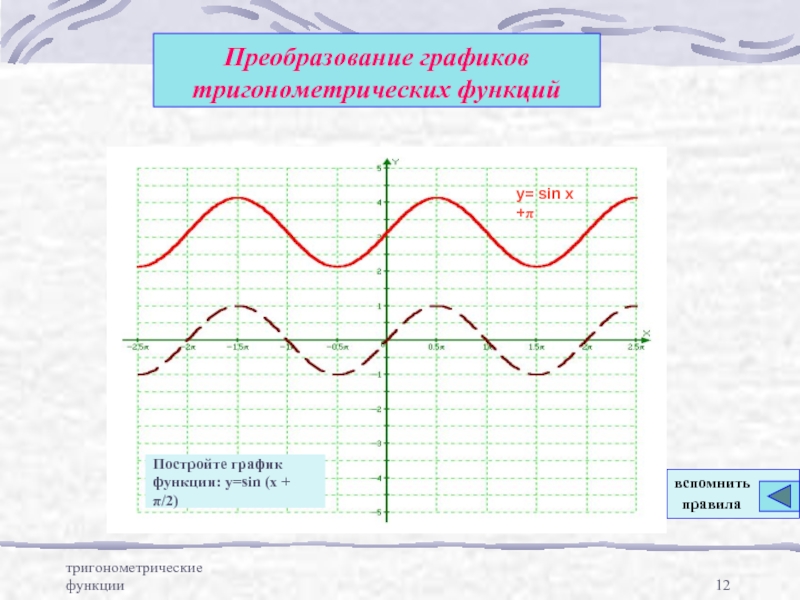
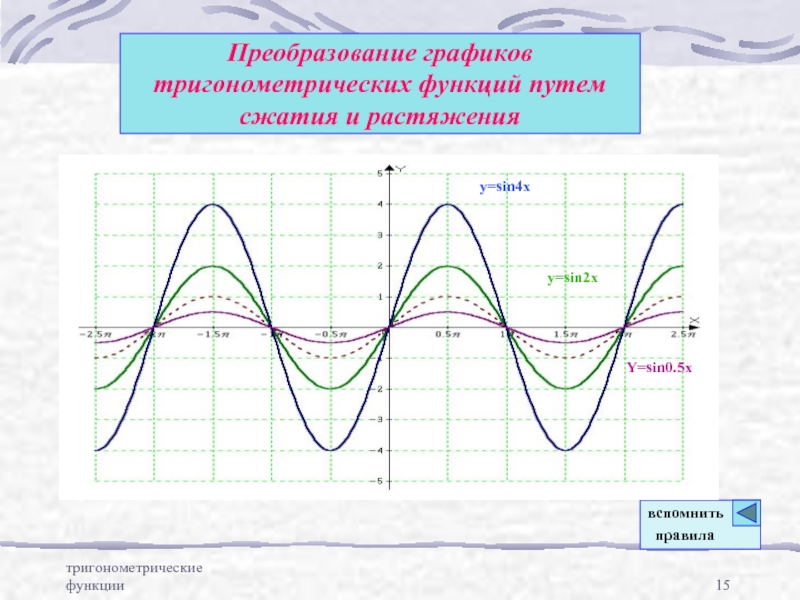
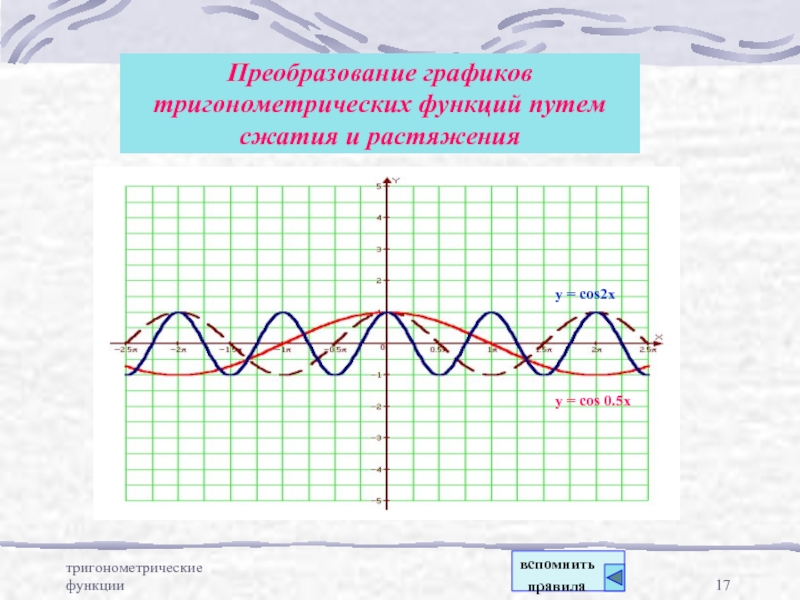
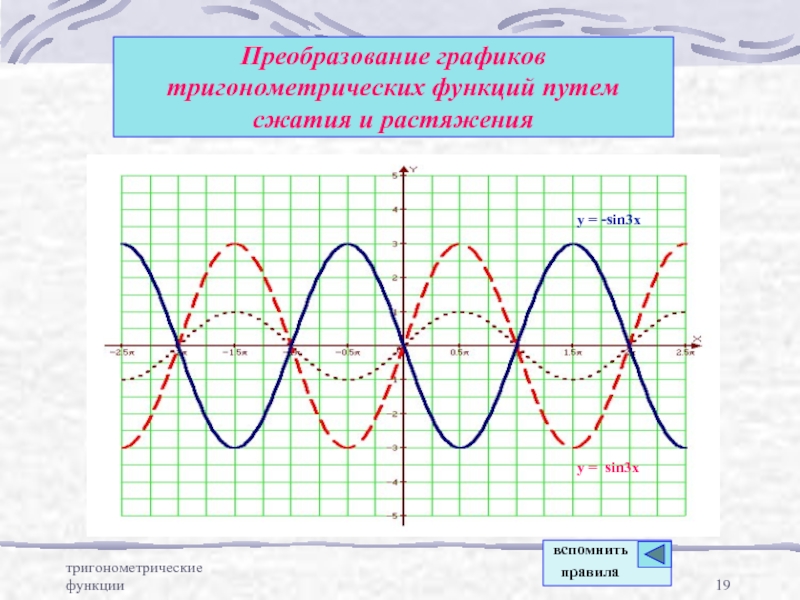
Преобразование графиков тригонометрических
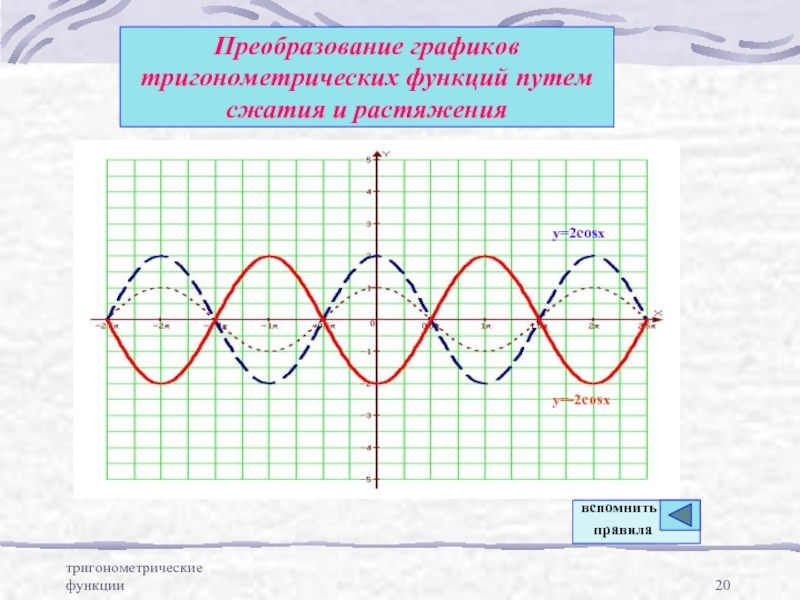
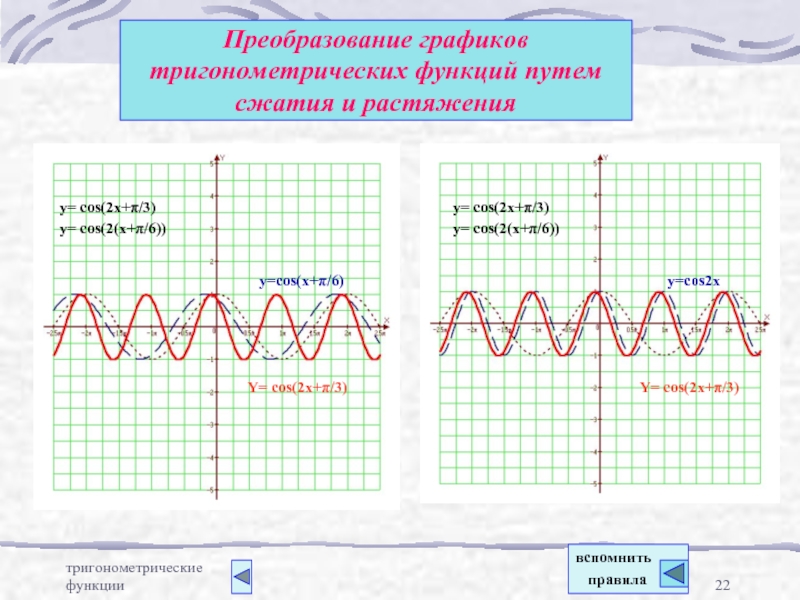
функций путем параллельного переносаПреобразование графиков тригонометрических функций путем сжатия и расширения
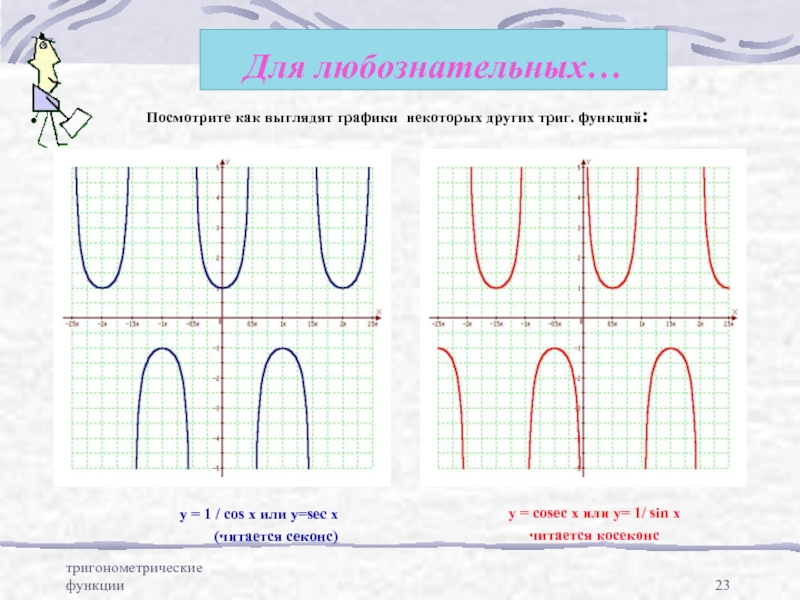
Для любознательных…


![Графики тригонометрических функций тригонометрические функцииСвойства функции у=sin x6. Промежутки монотонности:функция возрастает на промежутках вида: тригонометрические функцииСвойства функции у=sin x6. Промежутки монотонности:функция возрастает на промежутках вида: [-π/2+2πn; π/2+2πn], n∈Zy = sin x](/img/tmb/1/46324/d13c73ac5420fc7b14f2e7900ed04844-800x.jpg)
![Графики тригонометрических функций тригонометрические функцииСвойства функции у=sin x Промежутки монотонности:функция убывает на промежуткахвида: [π/2+2πn; 3π/2+2πn], n∈Zy=sin x тригонометрические функцииСвойства функции у=sin x Промежутки монотонности:функция убывает на промежуткахвида: [π/2+2πn; 3π/2+2πn], n∈Zy=sin x](/img/thumbs/46fdf429d863a7675b90cf39815cafc1-800x.jpg)
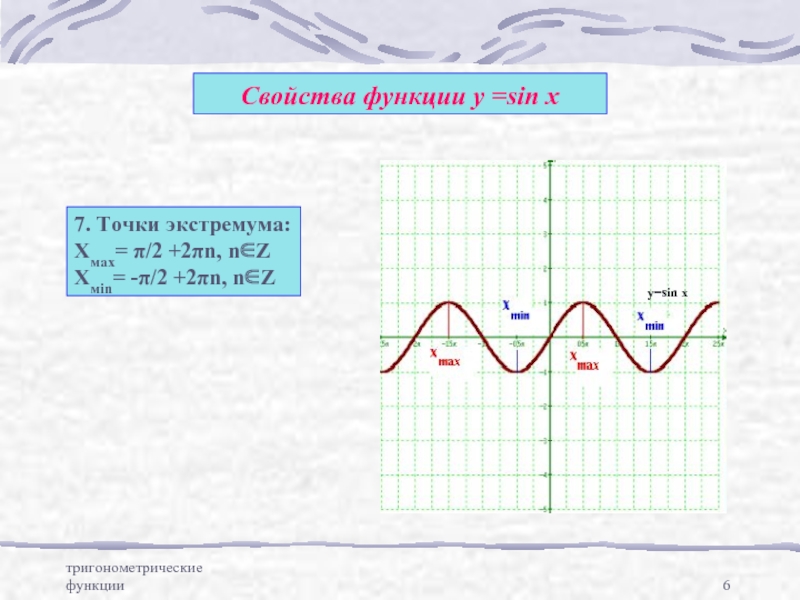
![Графики тригонометрических функций тригонометрические функцииСвойства функции у =sin x8. Область значений: Е(у) = [-1;1]y = sin x тригонометрические функцииСвойства функции у =sin x8. Область значений: Е(у) = [-1;1]y = sin x](/img/thumbs/33c11968c2cb4e16d0dcadfc1d3e9669-800x.jpg)