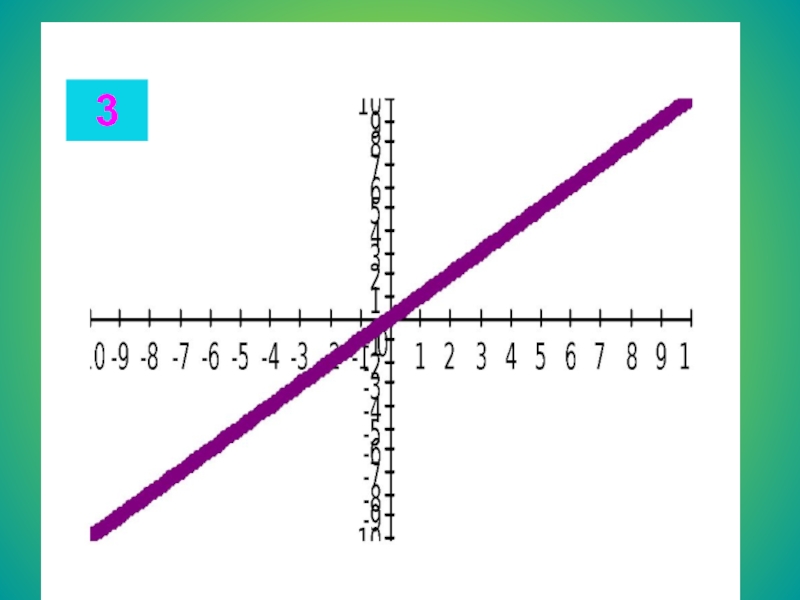
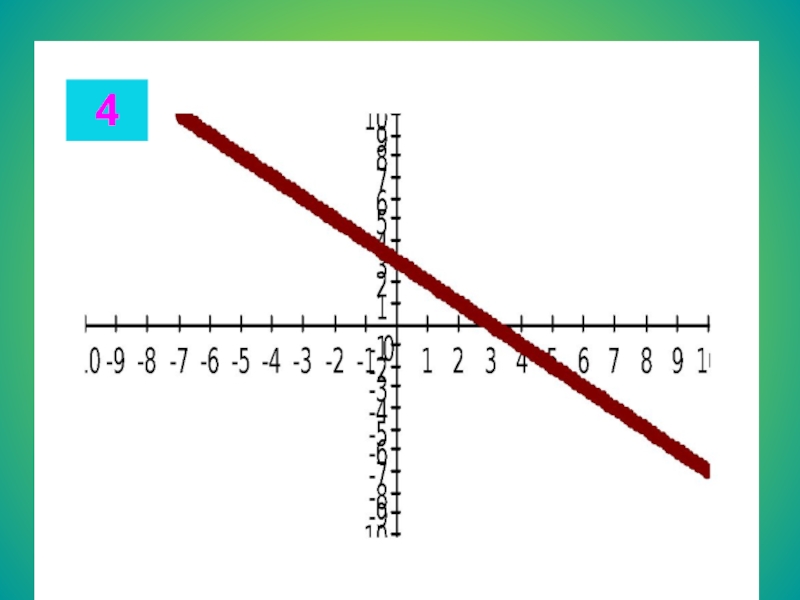
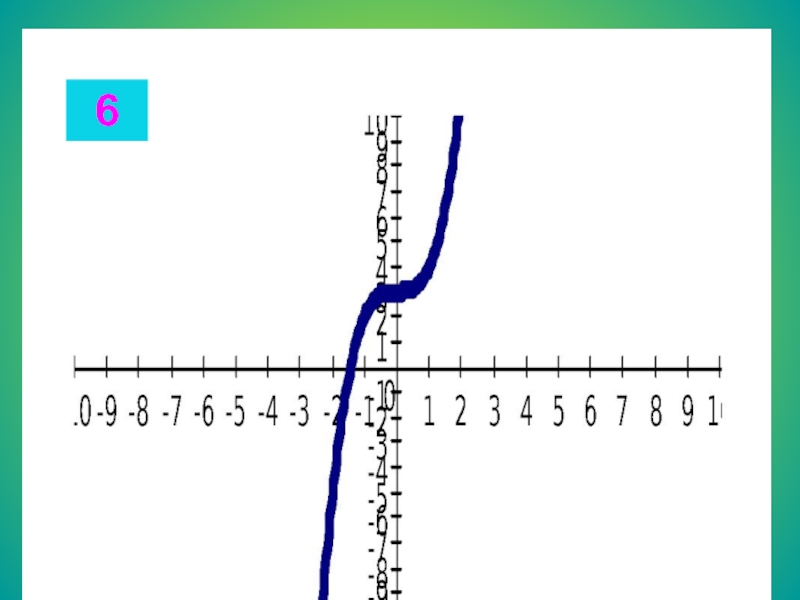
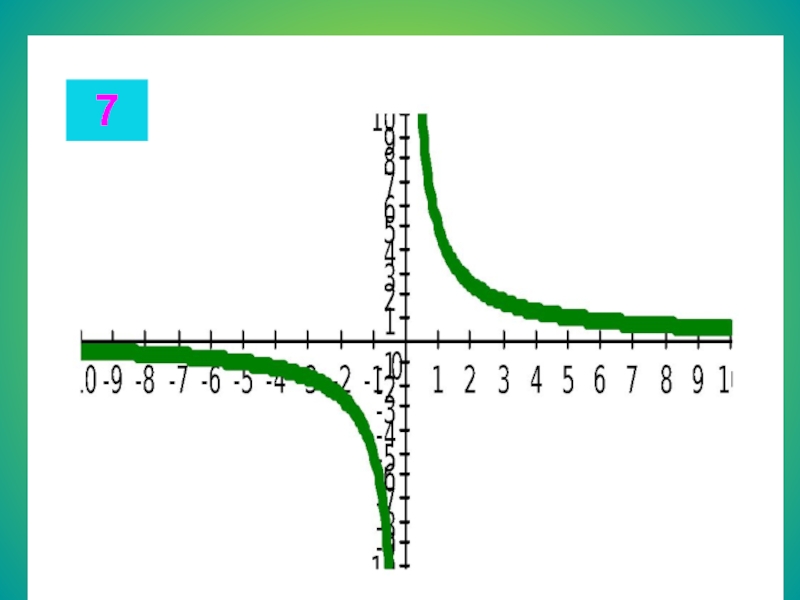
ж) x3 – 25x = 0
б)
3x – 5 = 0 з) x(x – 1)(x + 2) = 0в) x2 – 5 = 0 и) x4 – x2 = 0
г) x2 = 1/36 к) x2 – 0,01 = 0,03
д) x2 = – 25 л) 19 – c2 = 10
е) = 0 м) (x – 3)2 = 25
1) х – 3 = 5 и 2) х – 3 = – 5
Какие из этих уравнений не являются целыми?