Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения и неравенства с двумя переменными
Содержание
- 1. Уравнения и неравенства с двумя переменными
- 2. Уравнения и неравенства с двумя переменными Ребята,
- 3. Уравнения и неравенства с двумя переменными Для
- 4. Уравнения и неравенства с двумя переменными Рассмотрим
- 5. Уравнения и неравенства с двумя переменными Пример.
- 6. Уравнения и неравенства с двумя переменными Рассмотрим каждый
- 7. Уравнения и неравенства с двумя переменными Пример.
- 8. Уравнения и неравенства с двумя переменными Значит,
- 9. Уравнения и неравенства с двумя переменными Перейдем к
- 10. Уравнения и неравенства с двумя переменными Пример. Решить
- 11. Уравнения и неравенства с двумя переменными Можно подставить
- 12. Уравнения и неравенства с двумя переменными Пример. Решить неравенствоxy
- 13. Уравнения и неравенства с двумя переменными Нам
- 14. Уравнения и неравенства с двумя переменными Для
- 15. Уравнения и неравенства с двумя переменными Решения неравенства y≤x+5 расположены ниже прямой y=x+5.
- 16. Уравнения и неравенства с двумя переменными Изобразим
- 17. Уравнения и неравенства с двумя переменными Задачи
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Занимательная математика
Алгебра и начала математического анализа, 11 класс.
Урок на тему:
Уравнения
и неравенства с двумя переменными.
Слайд 2Уравнения и неравенства с двумя переменными
Ребята, мы разобрались с
уравнениями и неравенствами с одной переменной, теперь давайте перейдем к
более общему и сложному случаю к уравнениям и неравенствам с двумя переменными.Решением уравнения с двумя переменными P(x;y)=0 называется всякая пара чисел (x;y), которая обращает уравнение в верное числовое равенство.
При решении таких уравнений требуется проводить внимательный анализ уравнения и выявлять закономерности. Чаще всего, не существует общих методов решения уравнения с двумя переменными, к каждому уравнению нужен “индивидуальный подход”. Обычно решений получается бесконечно много.
Но стоит отметить, что переход к геометрической модели решения – на декартовой системе координат (как раз, на которой отмечаются две переменные) изображают все множество решений, является одним из самых удобных методов решения.
Слайд 3Уравнения и неравенства с двумя переменными
Для уравнения решение удовлетворяет
всякая пара чисел, такие, что они принадлежат окружности радиуса 4
и центром с координатами (0;0). Проще всего изобразить графически решение данного уравнения. В данном примере мы получили бесконечное число решений, которые удовлетворяют условию выше.
Слайд 4Уравнения и неравенства с двумя переменными
Рассмотрим другой пример ,
уравнение имеет всего одно решение х=-2 и у=-4, так как
сумма двух не отрицательных чисел может равняться нулю, когда они одновременно равны нулю. В данном примере мы получили всего одно решение.Если дано целое рациональное уравнение с несколькими переменными и целочисленными коэффициентами, и так же требуется найти целые (или рациональные) решения данного уравнения, то принято говорить, что задано диофантово уравнение.
Диофантовы уравнения решаются довольно таки трудно, и не всегда сразу можно придумать ходы решения сразу, но часто помогает теория делимости целых чисел. Так же отметим, что современные методы программирования позволяют решать многие уравнения на компьютерах, используя так называемые численные методы, с которыми вы можете познакомиться в университете, если пойдете учиться на математические специальности.
Слайд 5Уравнения и неравенства с двумя переменными
Пример. Найти целочисленные решения
уравнения:
5x+4y=17
Решение. В общем случае мы могли изобразить прямую, на декартовой
системе координат, и получить множество всех решений, но нам требуется найти только целочисленные решения.Воспользуемся известными предложениями теории делимости целых чисел.
Приведем наше уравнение к виду:
Целое число 17-5х должно делиться без остатка на 4. При делении на 4 возможны четыре случая:
а) остаток от деления на 4 равен нулю, то есть х=4k
б) остаток от деления на 4 равен единице, то есть х=4k+1
в) остаток от деления на 4 равен двум, то есть х=4k+2
г) остаток от деления на 4 равен трем, то есть х=4k+3, где k - целое число.
Слайд 6Уравнения и неравенства с двумя переменными
Рассмотрим каждый случай отдельно:
а) Если
х=4k, то - не делится нацело на 4, т.к. каждый
член разности должен делиться на 4, а число 17 не делится на 4.б) Если х=4k+1, то - делится нацело на 4.
в) Если х=4k+2, то – не делится на 4.
г) Если х=4k+3, то - не делится на 4.
Среди всех возможных вариантов нам подошел лишь один х=4k+1, тогда найдем y.
Целым решением нашего уравнения является любая пара чисел (4k+1;3-5k), где k – любое целое число.
Ответ: (4k+1;3-5k).
Слайд 7Уравнения и неравенства с двумя переменными
Пример. Найти целочисленные решения
уравнения:
Решение. Воспользуемся формулой разности квадратов
Мы получили произведение двух чисел в
левой части уравнения, и в правой части уравнения заметим, что у нас записано простое число, которое делится только на себя и единицу по модулю.Число 13 получается лишь в четырех случаях при произведении двух чисел:
а) Первый сомножитель равен 1, второй сомножитель равен 13.
б) Первый сомножитель равен 13, второй сомножитель равен 1.
в) Первый сомножитель равен -1, второй сомножитель равен -13.
г) Первый сомножитель равен -13, второй сомножитель равен -1.
Слайд 8Уравнения и неравенства с двумя переменными
Значит, нам надо решить
совокупность 4 систем.
а) б) в) г)
Решением каждой системы у нас служат пара чисел:
а)
(1.75;3) б) (1.75;-3) в) (-1.75;-3) г) (-1.75;3)В данном примере, целочисленных решений получается, что нет, но суть метода решения должна быть ясна.
Ответ: целочисленных решений нет.
Слайд 9Уравнения и неравенства с двумя переменными
Перейдем к неравенствам.
Неравенства вида
p(x;y)>0, p(x;y)
– алгебраическое выражение. Решением неравенства p(x;y)>0 называют всякую пару чисел, которые удовлетворяют данному неравенству (неравенство превращается в верное числовое неравенство). Решения неравенств с двумя переменными опять же проще изображать на графиках в декартовой системе координат. Рассмотрим несколько примеров.
Слайд 10Уравнения и неравенства с двумя переменными
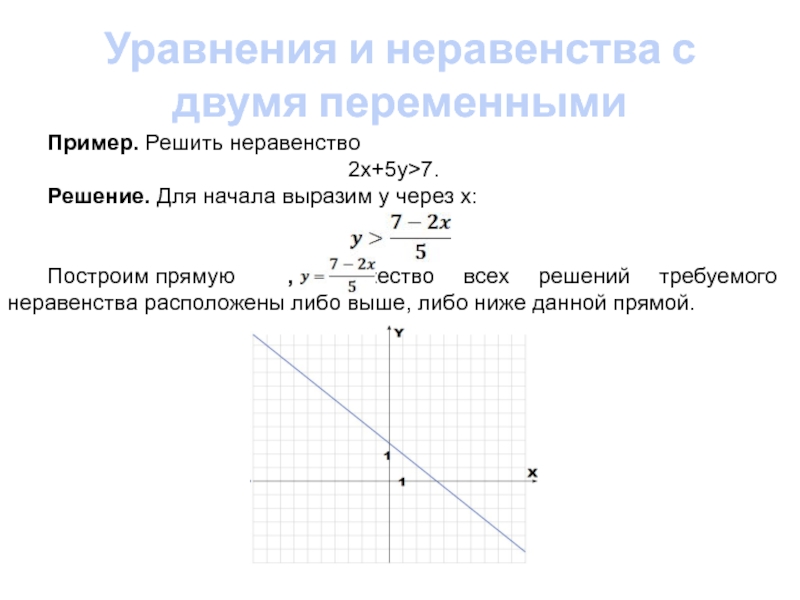
Пример. Решить неравенство
2x+5y>7.
Решение. Для
начала выразим у через х:
Построим прямую , множество всех решений
требуемого неравенства расположены либо выше, либо ниже данной прямой.
Слайд 11Уравнения и неравенства с двумя переменными
Можно подставить любую пару чисел
и проверить выполнилось неравенство или нет, если неравенство выполнилось, то
мы и выбираем в качестве решения ту область, которой принадлежат эти пара чисел, если не выполнилось, то выбираем противоположную область.Давайте подставим пару (1;2)
2>1 – верное неравенство.
Значит, мы должны выбрать область выше нашей прямой, область в которой выполняется наше неравенство, обычно принято изображать штриховкой.
Слайд 12Уравнения и неравенства с двумя переменными
Пример. Решить неравенство
xy
возможных случая
а) х=0, то получаем верное неравенство 0
неравенство выполняется для любых у если х=0.б) х>0, перейдем к неравенству y<3/x – данному неравенству, в правой полуплоскости, удовлетворяют множество всех точек ниже прямой y=3/x.
в) x<0, перейдем к неравенству y>3/x – данному неравенству, в левой полуплоскости удовлетворяют множество всех точек выше прямой y=3/x.
Нам осталось построить график
функции и отметить множество всех решений:
Слайд 13Уравнения и неравенства с двумя переменными
Нам осталось разобрать пример,
решения системы неравенств с двумя переменными. Суть метода решений проста,
находим решение каждого неравенства в отдельности, изображаем решения на одной координатной плоскости и ищем пересечение этих решений.Пример. Решить систему неравенств:
Решение. Найдем решение каждого неравенства в отдельности.
Слайд 14Уравнения и неравенства с двумя переменными
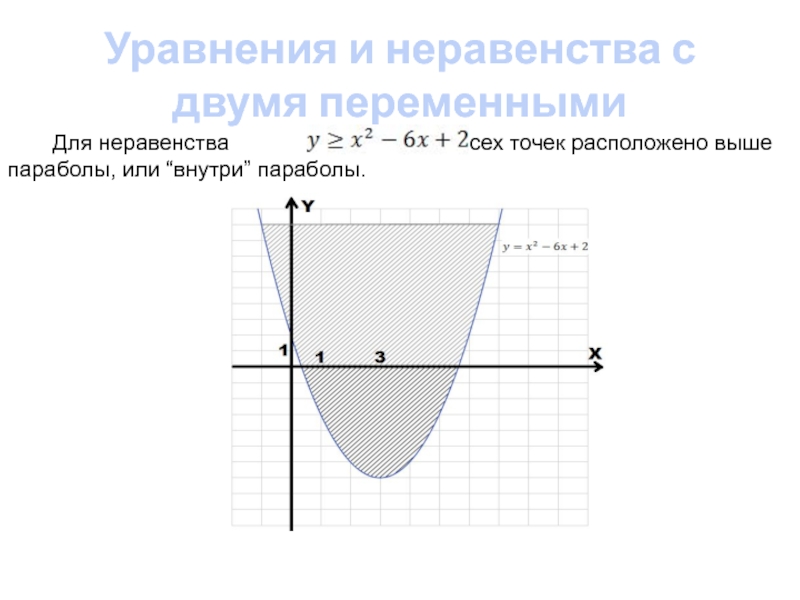
Для неравенства , множество
всех точек расположено выше параболы, или “внутри” параболы.
Слайд 15Уравнения и неравенства с двумя переменными
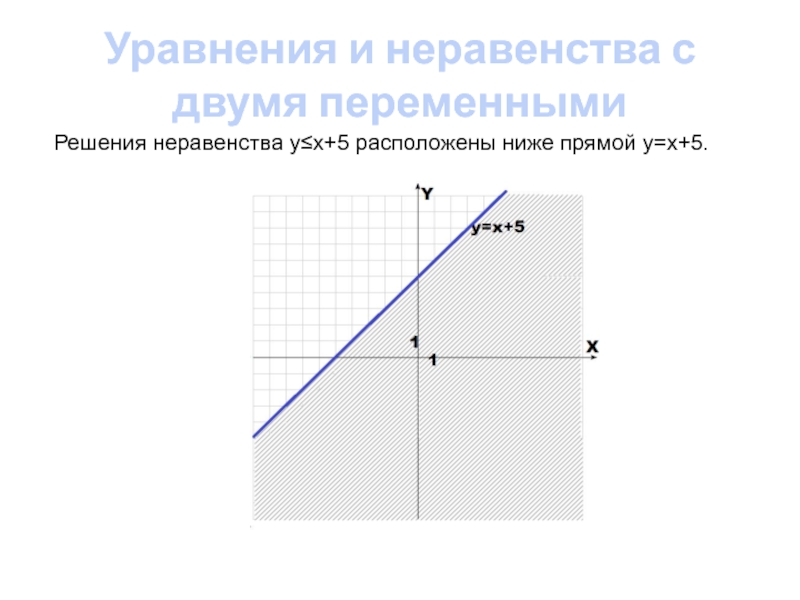
Решения неравенства y≤x+5 расположены
ниже прямой y=x+5.
Слайд 16Уравнения и неравенства с двумя переменными
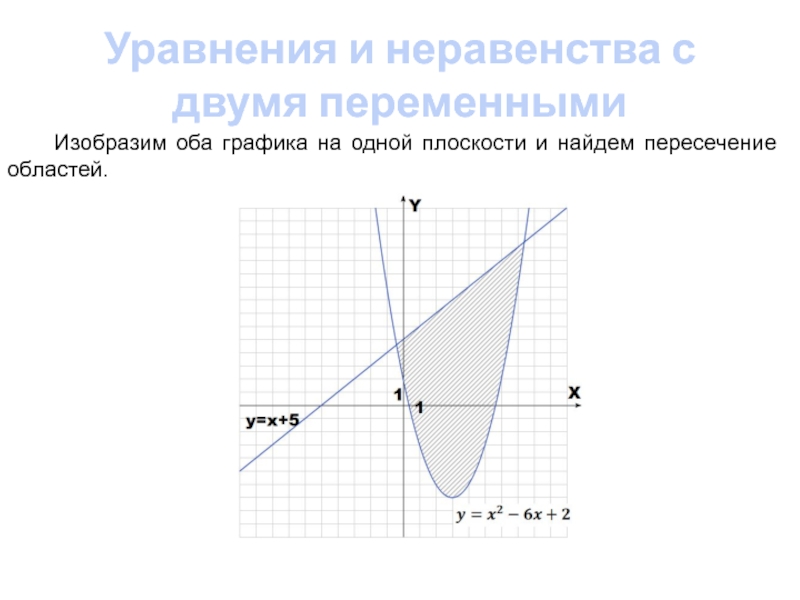
Изобразим оба графика на
одной плоскости и найдем пересечение областей.
Слайд 17Уравнения и неравенства с двумя переменными
Задачи для самостоятельного решения.
1.
Найти целочисленные решения уравнения: 7x+5y=15
2. Найти целочисленные решения уравнения:
3. Решить
неравенство: xy>7.4. Решить систему неравенств: