Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Касательная к окружности 7 класс
Содержание
- 1. Касательная к окружности 7 класс
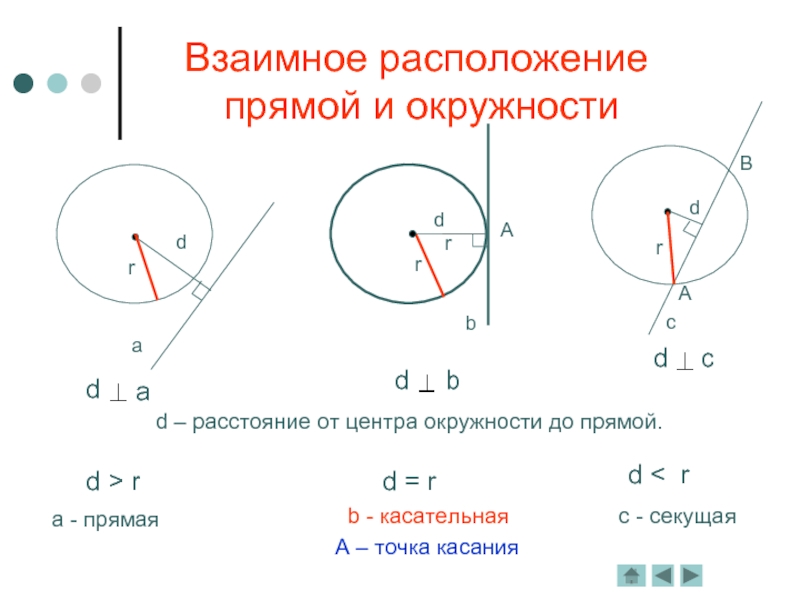
- 2. Взаимное расположение прямой и окружностиd – расстояние от центра окружности до прямой.
- 3. ORSCMKFTADBQNXНазови: радиус, диаметр, хорду, касательную, секущую
- 4. Теорема. Касательная к окружности перпендикулярна к
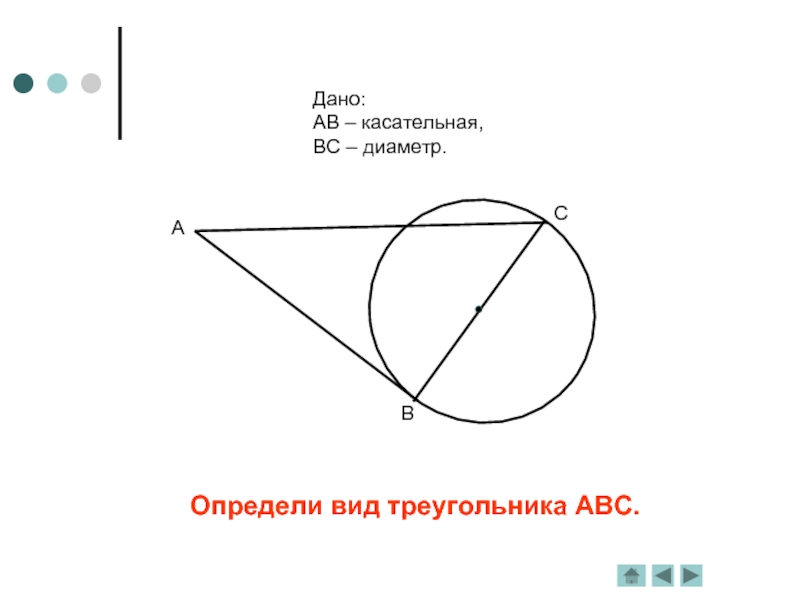
- 5. Определи вид треугольника АВС.Дано:АВ – касательная,ВС – диаметр.
- 6. тестСколько касательных можно провести через данную точку
- 7. 3. Сколько окружностей можно провести, касающихся данной
- 8. 4. Сколько окружностей можно провести, касающихся данной
- 9. 5. Сколько окружностей данного радиуса можно провести,
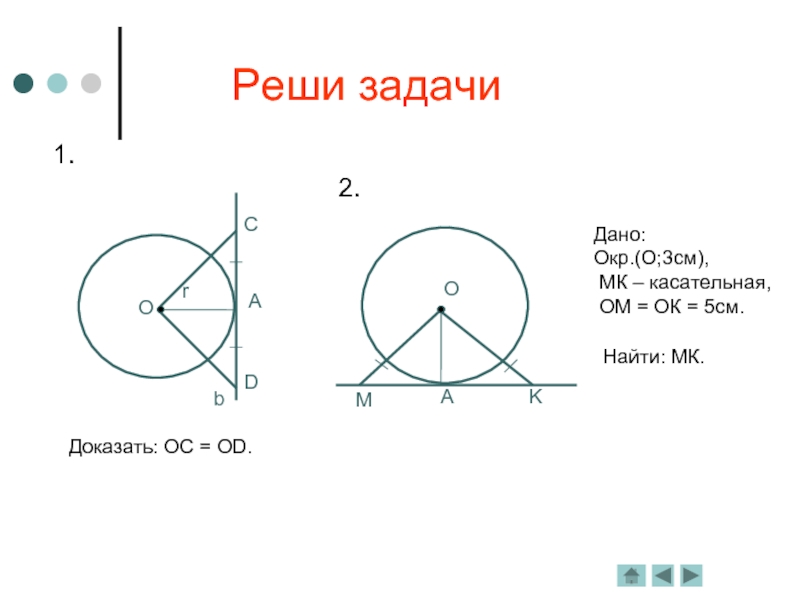
- 10. Реши задачи
- 11. Важное свойствоОтрезки касательных к окружности, проведённые из
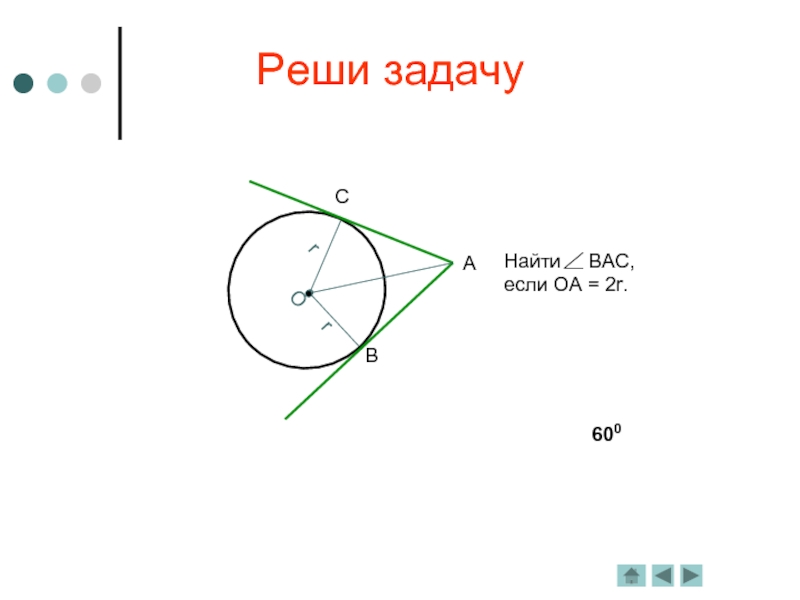
- 12. Реши задачу600
- 13. Реши задачуАВ = АС
- 14. Реши задачу
- 15. Реши задачу
- 16. Реши задачу1 : 1
- 17. Если прямая проходит через конец радиуса, лежащий
- 18. Реши задачуДоказать, что все стороны треугольника КНМ касаются окружности.
- 19. Желаю успехов в учёбе!Михайлова Л. П.ГОУ ЦО № 173.
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Теорема. Касательная к окружности перпендикулярна к
радиусу, проведённому в точку касания.
Дано: Окр.(О;r),
р – касательная,А – точка касания.
Доказательство:
А – точка касания, О – центр окружности, значит, ОА – радиус.
Пусть касательная р не перпендикулярна ОА, тогда
радиус ОА является наклонной к прямой р.
Тогда перпендикуляр, проведённый из точки О к прямой р,
меньше наклонной ОА, т. е. расстояние от центра окружности
меньше радиуса.
Значит, прямая р и окружность будут иметь две общих точки, но это
противоречит условию: р – касательная, т. е. она имеет с окружностью одну
общую точку.
Следовательно, предположение, что р не перпендикулярна ОА неверно.
Касательная к окружности
Определение. Прямая, имеющая с окружностью одну общую
точку, называется касательной.
Слайд 6тест
Сколько касательных можно провести через данную точку
на
окружности ?
а) одну; б) две;
в) бесконечно много.2. Сколько касательных можно провести через точку, не лежащую
на окружности ?
а
а) одну; б) две; в) бесконечно много.
б
.
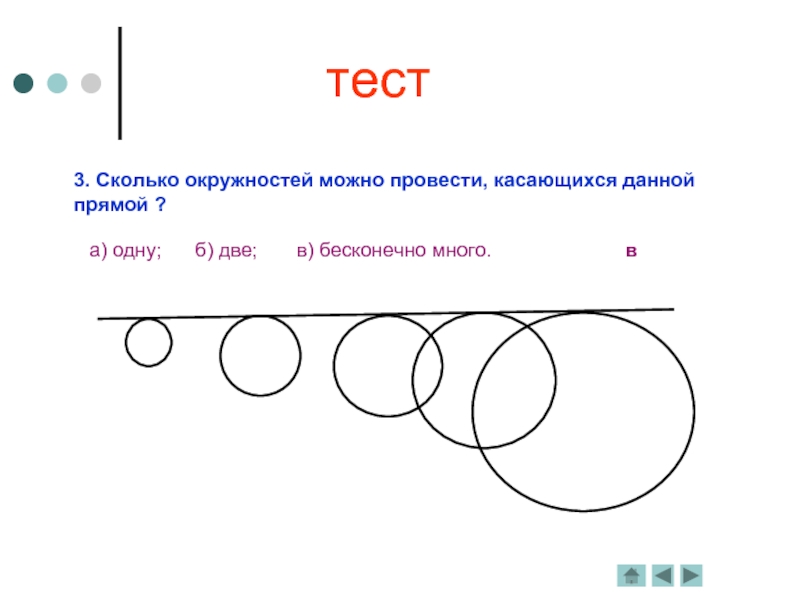
Слайд 73. Сколько окружностей можно провести, касающихся данной прямой ?
а) одну;
б) две; в) бесконечно много.
в
тест
Слайд 8
4. Сколько окружностей можно провести, касающихся данной прямой в данной
точке ?
в
а) одну; б) две;
в) бесконечно много.тест
Слайд 95. Сколько окружностей данного радиуса можно провести, касающихся данной прямой
в данной точке ?
а) одну; б) две;
в) бесконечно много.б
тест
Слайд 11
Важное свойство
Отрезки касательных к окружности, проведённые из одной точки, равны
и составляют равные углы с прямой, проходящей через эту точку
и центрокружности.
Дано: Окр.(О; r), АВ и АС – касательные.
Дополнительные свойства:
3. СК = ВК.
Слайд 17Если прямая проходит через конец радиуса,
лежащий на окружности, и
перпендикулярна
к этому радиусу, то она является касательной.
(теорема, обратная к
свойству касательной)Признак касательной
Доказать: АВ – касательная.
Доказательство:
и, следовательно, прямая и окружность имеют
только одну общую точку.
По определению касательной и будет прямая АВ.