Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Простейшие задачи в координатах. Скалярное произведение векторов
Содержание
- 1. Простейшие задачи в координатах. Скалярное произведение векторов
- 2. Цели урока:Образовательная;Развивающая;Воспитательная.
- 3. Образовательная: Отработка навыков и умений решения
- 4. Развивающая:Формирование умений выполнять обобщение; развитие качеств мышления: целенаправленность, рациональность; развитие самостоятельной деятельности учащихся на уроке.
- 5. Воспитательная:Воспитание интереса и любви к предмету; умения работать в коллективе; культуры общения.
- 6. План урока:Организационный момент.Сообщение темы и цели урока.Повторение:
- 7. Повторение: Найти координаты вектора АВ, если
- 8. Вопрос:Как найти координаты вектора, если известны координаты его начала и конца?
- 9. Ответ: A ( x ;
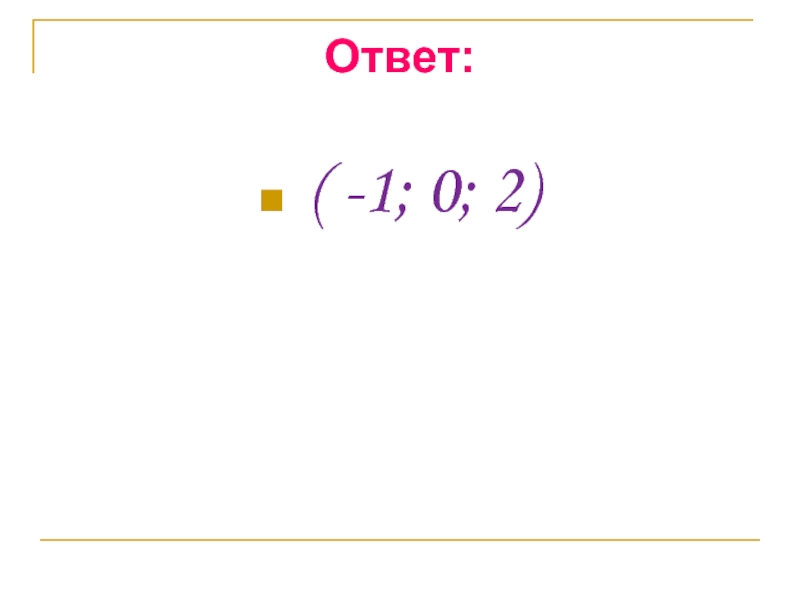
- 10. Ответ: ( -1; 0; 2)
- 11. Повторение:М – середина отрезка АВ. Найти координаты
- 12. Вопрос:Как найти координаты середины отрезка?
- 13. Ответ: A ( x ;
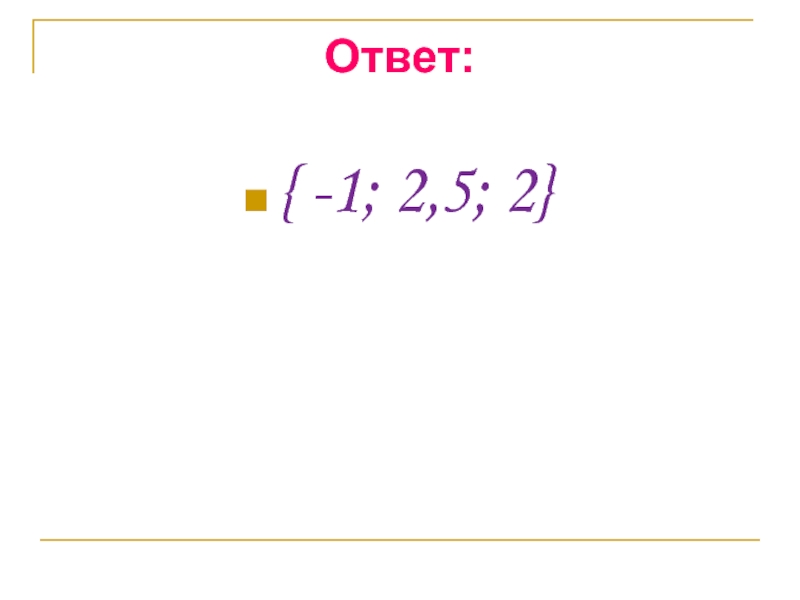
- 14. Ответ:{ -1; 2,5; 2}
- 15. Повторение:Найти длину вектора а, если он имеет координаты: {-5; -1; 7}.
- 16. Вопрос:Как вычислить длину вектора по его координатам?
- 17. Ответ:Координаты вектора a { x ; y
- 18. Ответ:5 корней квадратных из 3
- 19. Повторение:Найти расстояние между точками А и В,
- 20. Вопрос:Как вычислить расстояние между точками?
- 21. Ответ: A ( x ; y
- 22. Ответ:7 корней квадратных из 2
- 23. Повторение:Найти скалярное произведение векторов: а {1; -1; 2} и в {5; 6; 2}.
- 24. Вопрос:Что называется скалярным произведением векторов?
- 25. Ответ: Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 26. Вопрос: Как вычислить скалярное произведение векторов по их координатам?
- 27. Ответ: Вектор a { x
- 28. Ответ:3.
- 29. Решение задач:Доказать, что четырехугольник ABCD является ромбом,
- 30. Решение:
- 31. Решение задач: № 453.
- 32. Решение:
- 33. Решение задач: Даны точки: А(1;2;3); В(2;3;1) и С(3;1;2). Найти периметр треугольника АВС.
- 34. Решение:
- 35. Решение задач: (по карточкам)Найти расстояние между точками
- 36. Тест: I. Если М (-2; -4; 5),
- 37. Тест: II. Если А (5; 4; 0),
- 38. Тест:III. Если вектор а имеет координаты
- 39. Тест:IY. Если А(2; 7; 9), В(-2; 7;
- 40. Тест:Y. Скалярное произведение векторов а {-4; 3;
- 41. Тест:YI. Угол между векторами
- 42. Проверка: 3 1 2 3 2 2
- 43. Итог урока:Над какой темой работали?Что повторили?
- 44. Оценка работ:Краснобрыжева И.Мельникова Е.Музалев И.Саблина К.Теряева М.Тужилина О.Ягибеков Р.
- 45. Задание на дом: Глава 5, параграфы 1 – 2.
- 46. Скачать презентанцию
Цели урока:Образовательная;Развивающая;Воспитательная.
Слайды и текст этой презентации
Слайд 1«Простейшие задачи в координатах. Скалярное произведение векторов»
Решение задач
Урок геометрии в
11 классе
Слайд 3
Образовательная:
Отработка навыков и умений решения простейших задач в координатах и
решения задач на скалярное произведение векторов.
Слайд 4Развивающая:
Формирование умений выполнять обобщение; развитие качеств мышления: целенаправленность, рациональность; развитие
самостоятельной деятельности учащихся на уроке.
Слайд 5Воспитательная:
Воспитание интереса и любви к предмету; умения работать в коллективе;
культуры общения.
Слайд 6План урока:
Организационный момент.
Сообщение темы и цели урока.
Повторение: математический диктант с
повторением теории.
Решение задач.
Тест с последующей проверкой.
Итог урока.
Оценка работ.
Задание на дом.
Слайд 21Ответ:
A ( x ; y ; z )
B ( x
; y ; z )Вектор AB = [( x - x ) +
+ ( y - y ) + ( z - z ) ]
2
1
2
2
1
2
2
1
2
1/2
1
1
1
2
2
2
Слайд 25Ответ:
Скалярным произведением двух векторов называется произведение их длин
на косинус угла между ними.
Слайд 27Ответ:
Вектор a { x ; y
; z },
вектор в
{ x ; y ; z }Скалярное произведение
векторов
а в = x x + y y + z z
1
1
1
2
2
2
1
2
1
2
1
2
Слайд 29Решение задач:
Доказать, что четырехугольник ABCD является ромбом, если
A
(6; 7; 8), B (8; 2; 6),
C (4;
3; 2), D (2; 8; 4).Слайд 35Решение задач:
(по карточкам)
Найти расстояние между точками
В(-2;0;3) и
К(3;4;-2).
А(1;2;3) и В(3;-6;7). Найти координаты середины отрезка АВ.
Найти скалярное произведение
векторов а{1;2;4} и в{-8;2;1}.Найти угол между векторами a{1;2;-2} и
в{1;0;-1}.
Слайд 36Тест:
I. Если М (-2; -4; 5),
Р (-3;
-5; 2), то МР имеет координаты:
1. (1; 1;
3);2. (-5; -9; 7);
3. (-1; -1; -3).
Слайд 37Тест:
II. Если А (5; 4; 0), В (3; -6;
2) и С – середина отрезка, то С имеет координаты:
1. (4; -1; 1);2. (1; 5; -1);
3. (-1; -5; 1).
Слайд 38
Тест:
III. Если вектор а имеет координаты {-3; 3; 1}, то
его длина равна:
1. 1;
2. кв. корень
из 19;3. 0.
Слайд 39Тест:
IY. Если А(2; 7; 9), В(-2; 7; 1), то расстояние
между точками А и В равно:
1. 8;
2. кв. корень из 149;3. 4 корней из 5.