Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Окружность, вписанная в правильный многоугольник
Содержание
- 1. Окружность, вписанная в правильный многоугольник
- 2. Правильный n-угольникУгол правильногоn-угольника (αn)А1А2Ап1. Сумма всех углов правильногоn-угольника:2. Формула для вычисленияугла αп правильногоn-угольника :Повторим формулы:
- 3. Окружность R = 5 см касается сторон
- 4. Две окружности пересекаются в точках А и
- 5. Около любого правильного многоугольника можно описать окружность
- 6. В любой правильный многоугольник можно вписать окружность,
- 7. ●О 1. Окружность, вписанная в правильный многоугольник,
- 8. Выберите правильное утверждение:Многоугольник является правильным, если
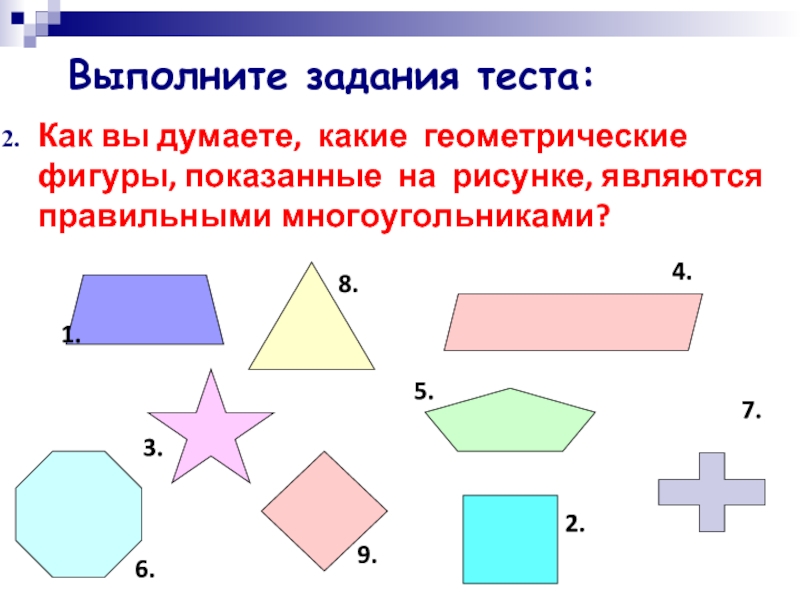
- 9. Как вы думаете, какие геометрические фигуры, показанные на рисунке, являются правильными многоугольниками?1.2.3.4.5.6.7.8.9.Выполните задания теста:
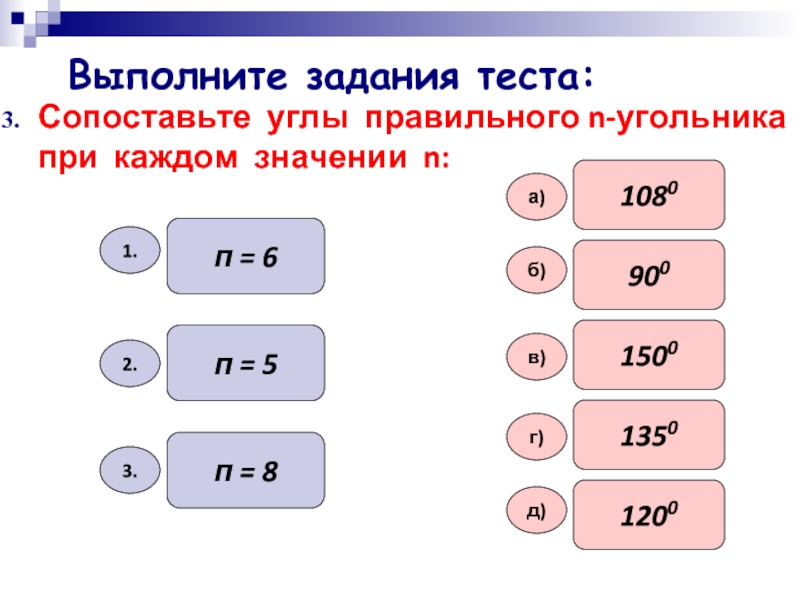
- 10. Сопоставьте углы правильного n-угольника при каждом значении n:п = 6п = 5п = 812001080150090013501.3.2.а)б)в)г)д)Выполните задания теста:
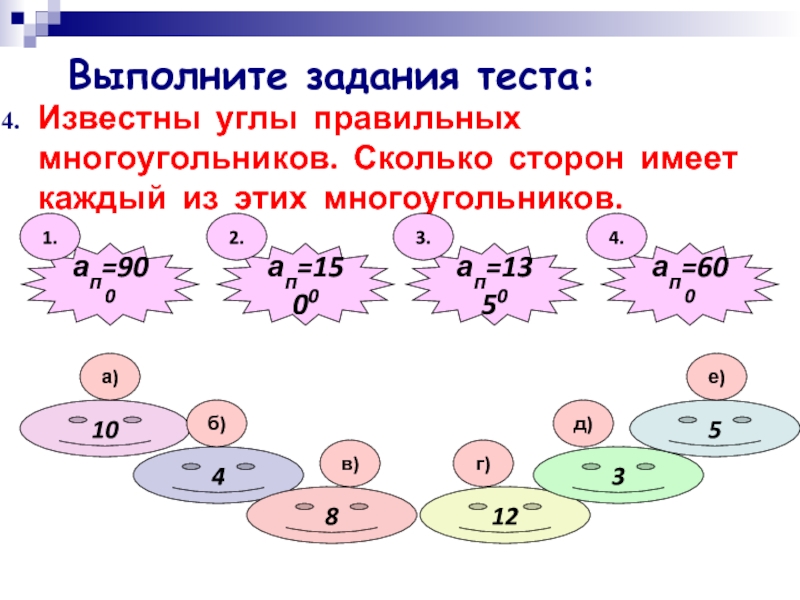
- 11. Известны углы правильных многоугольников. Сколько сторон имеет каждый из этих многоугольников.ап=1350ап=1500ап=900ап=600412385101.4.3.2.а)б)в)г)д)е)Выполните задания теста:
- 12. Д/з:п.107;№1131; №1130
- 13. Скачать презентанцию
Правильный n-угольникУгол правильногоn-угольника (αn)А1А2Ап1. Сумма всех углов правильногоn-угольника:2. Формула для вычисленияугла αп правильногоn-угольника :Повторим формулы:
Слайды и текст этой презентации
Слайд 1Окружность, вписанная в правильный многоугольник
Козак Татьяна Ивановна,
учитель математики
МОБУ СОШ №20
пгт.Прогресс
Амурской области
Слайд 2
Правильный n-угольник
Угол правильного
n-угольника (αn)
А1
А2
Ап
1. Сумма всех углов правильного
n-угольника:
2. Формула для
вычисления
угла αп правильного
n-угольника :
Повторим формулы:
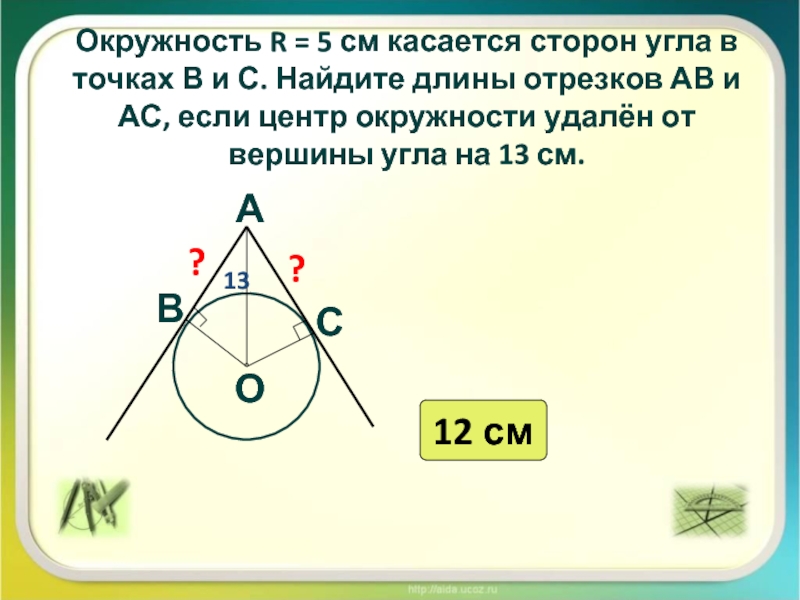
Слайд 3Окружность R = 5 см касается сторон угла в точках
В и С. Найдите длины отрезков АВ и АС, если
центр окружности удалён от вершины угла на 13 см.А
В
С
?
?
О
13
12 см
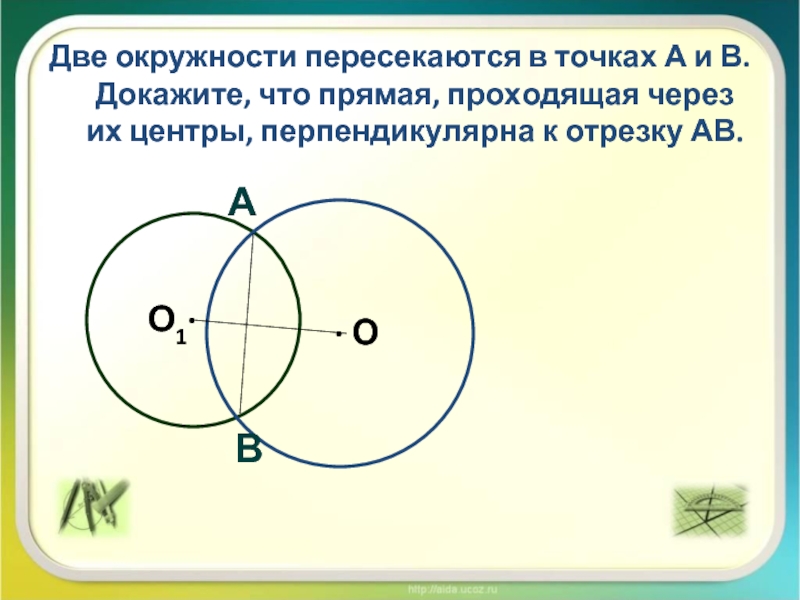
Слайд 4Две окружности пересекаются в точках А и В. Докажите, что
прямая, проходящая через их центры, перпендикулярна к отрезку АВ.
∙ О
О1∙
А
В
Слайд 5
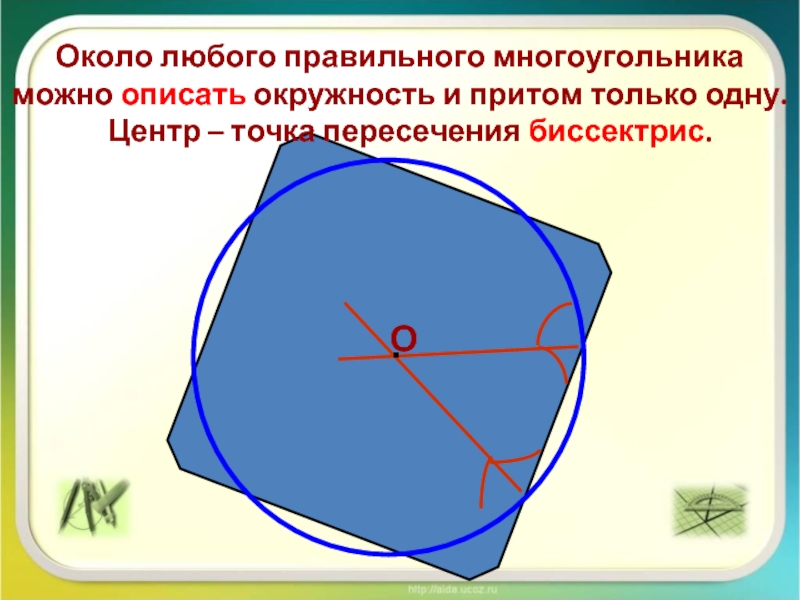
Около любого правильного многоугольника можно описать окружность и притом только
одну.
Центр – точка пересечения биссектрис.
·
О
Слайд 6
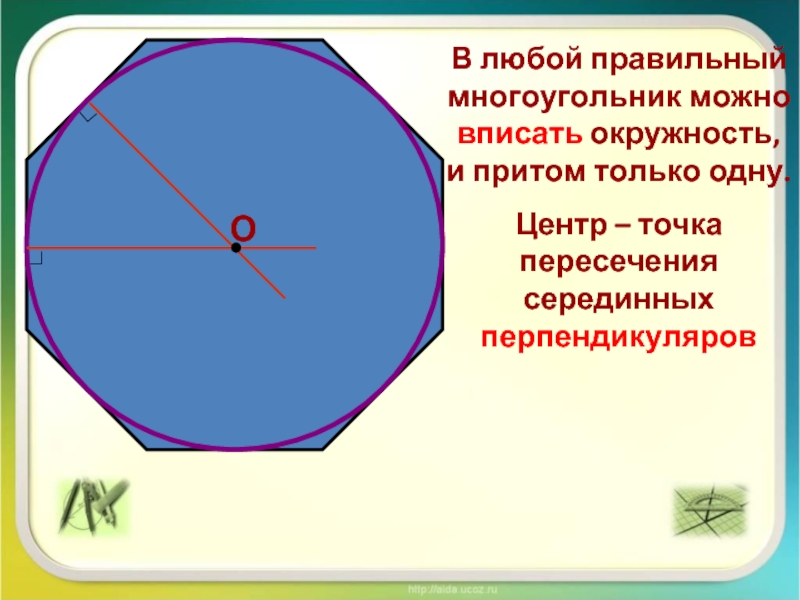
В любой правильный многоугольник можно вписать окружность, и притом только
одну.
Центр – точка пересечения серединных перпендикуляров
•
О
∟
∟
Слайд 7
●
О
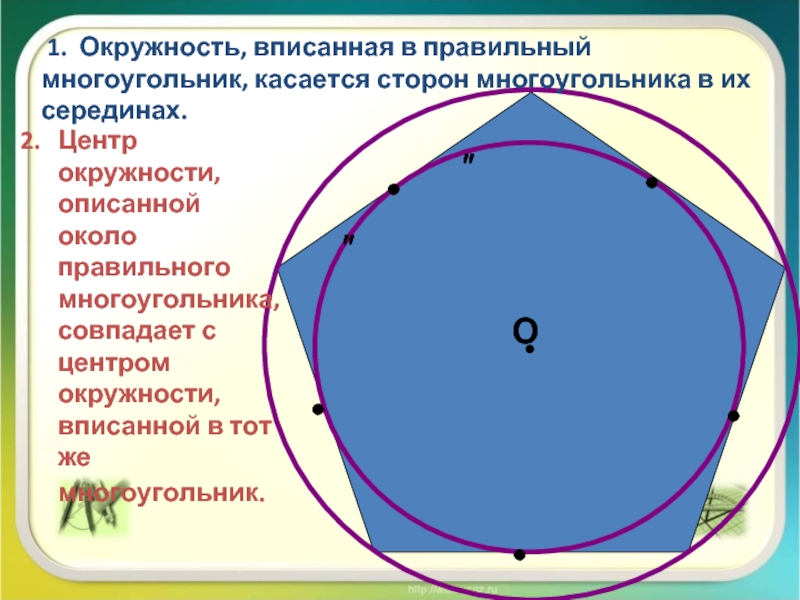
1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника
в их серединах.
●
●
●
●
●
″
″
Центр окружности, описанной около правильного многоугольника, совпадает с
центром окружности, вписанной в тот же многоугольник. 
Слайд 8Выберите правильное утверждение:
Многоугольник является правильным, если он выпуклый и
все его стороны равны.
Любой равносторонний треугольник является правильным.
Любой четырехугольник с
равными сторонами является правильным.Выполните задания теста:
Слайд 9Как вы думаете, какие геометрические фигуры, показанные на рисунке, являются
правильными многоугольниками?
1.
2.
3.
4.
5.
6.
7.
8.
9.
Выполните задания теста:
Слайд 10Сопоставьте углы правильного n-угольника при каждом значении n:
п = 6
п
= 5
п = 8
1200
1080
1500
900
1350
1.
3.
2.
а)
б)
в)
г)
д)
Выполните задания теста:
Слайд 11Известны углы правильных многоугольников. Сколько сторон имеет каждый из этих
многоугольников.
ап=1350
ап=1500
ап=900
ап=600
4
12
3
8
5
10
1.
4.
3.
2.
а)
б)
в)
г)
д)
е)
Выполните задания теста:
