Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Центральная и осевая симметрии 8 класс
Содержание
- 1. Центральная и осевая симметрии 8 класс
- 2. План урокаТеоретическая самостоятельная работа с самопроверкой.Изучение нового
- 3. Ответы к тестуВариант №1.Ч В заданиях вставьте
- 4. Ответы к тестуВариант №1.1 г2 г3 г4
- 5. Центральная и осевая симметрии
- 6. Слайд 6
- 7. Точки А и А1 называются симметричными относительно
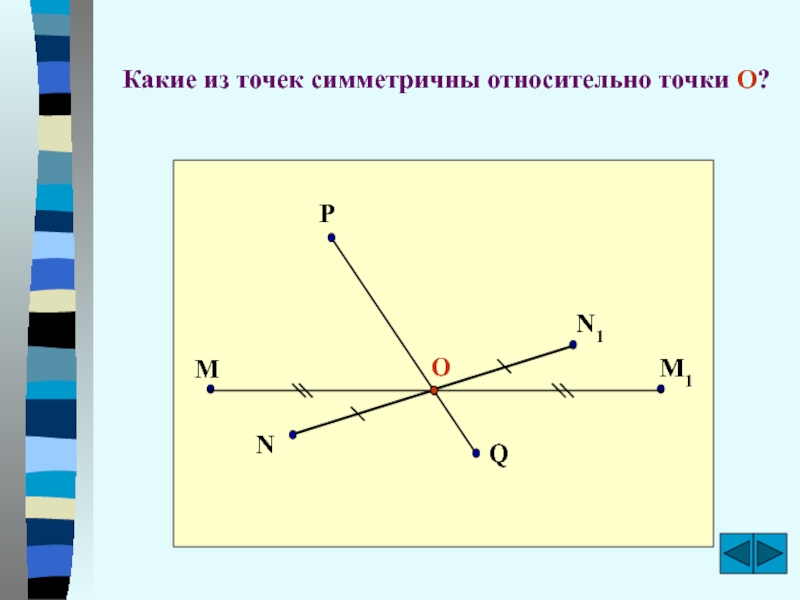
- 8. Какие из точек симметричны относительно точки О?NN1ОMM1QP
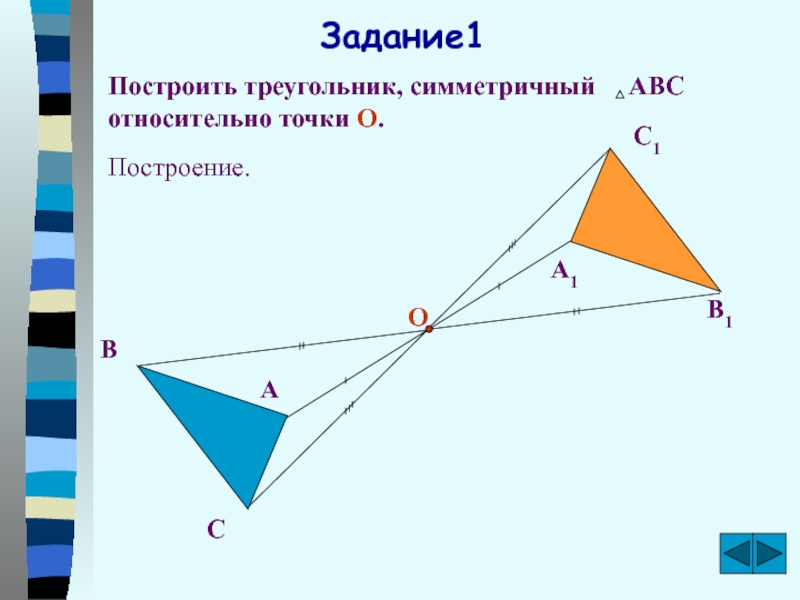
- 9. Задание1Построить треугольник, симметричный АВС относительно точки О. ОВАСА1С1В1Построение.
- 10. Фигура называется симметричной относительно
- 11. Осевая симметрия Две точки А и
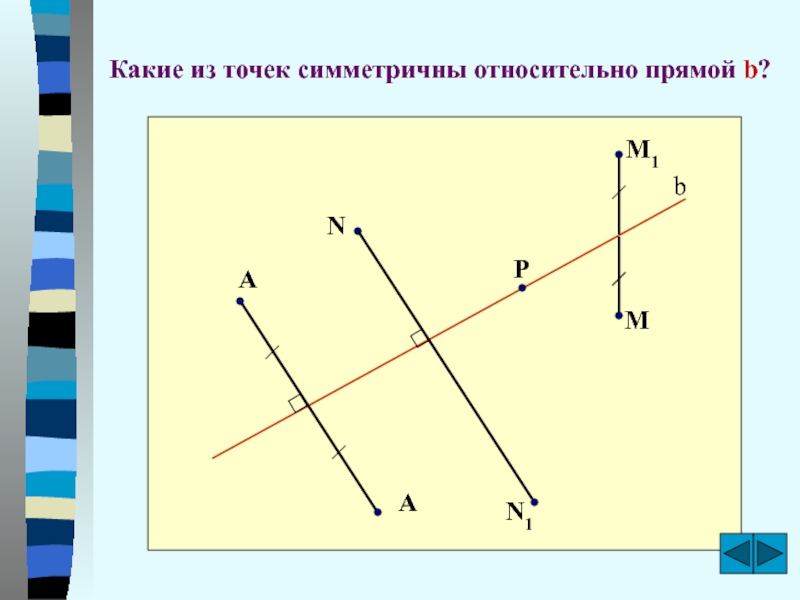
- 12. Какие из точек симметричны относительно прямой b?bNN1MM1AAP
- 13. bСВАА1В1С1Задание 2Построить треугольник, симметричный АВС относительно прямой b Построение.
- 14. Фигура называется симметричной относительно
- 15. Примеры фигур, обладающих центральной и осевой симметрией.
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2План урока
Теоретическая самостоятельная работа с самопроверкой.
Изучение нового материала с
использованием презентации.
Слайд 3Ответы к тесту
Вариант №1.
Ч В заданиях вставьте пропущенные слова в
определениях и теоремах.
1. *** называется фигура, которая состоит из четырех
точек и четырех последовательно соединяющих их отрезков.а) прямоугольник б) трапеция
в) ромб г) четырехугольник
2.Прямоугольник – это ***, у которого все углы прямые.
а) трапеция б) четырехугольник
в) ромб г) параллелограмм
3. Диагонали ромба являются *** его углов.
а) медианами б) высотами в) средними линиями г) биссектрисами
4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны.
а) прямоугольник б) параллелограмм
в) трапеция г) ромб
5. У параллелограмма противолежащие стороны равны, противолежащие *** равны.
а) вершины б) углы в) прямые г) отрезки
6. Ромб – это ***, у которого все стороны равны.
а) четырехугольник б) прямоугольник
в) квадрат г) параллелограмм
7. *** параллелограмма пересекаются и точкой пересечения делятся пополам.
а) вершины б) стороны в) углы г) диагонали
8. Диагонали *** равны.
а) четырехугольника б) ромба
в) прямоугольника г) трапеции
Вариант №2.
В заданиях вставьте пропущенные слова в определениях и теоремах.
1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков.
а) четырехугольник б) трапеция
в) ромб г) прямоугольник
2.Прямоугольник – это ***, у которого все углы прямые.
а) трапеция б) параллелограмм
в) ромб г) четырехугольник
3. Диагонали ромба являются *** его углов.
а) медианами б) высотами в) биссектрисами г) средними линиями
4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны.
а) прямоугольник б) трапеция
в) параллелограмм г) ромб
5. У параллелограмма противолежащие стороны равны, противолежащие *** равны.
а) вершины б) отрезки в) прямые г) углы
6. Ромб – это ***, у которого все стороны равны.
а) параллелограмм б) прямоугольник
в) квадрат г) четырехугольник
7. *** параллелограмма пересекаются и точкой пересечения делятся пополам.
а) вершины б) диагонали в) углы г) стороны
8. Диагонали *** равны.
а) четырехугольника б) прямоугольника
в) ромба г) трапеции
Слайд 7
Точки А и А1 называются симметричными относительно точки О, если
О - середина отрезка АА1.
О - центр симметрии
А
А1
О
Точка О
считается симметричной самой себе.Центральная симметрия
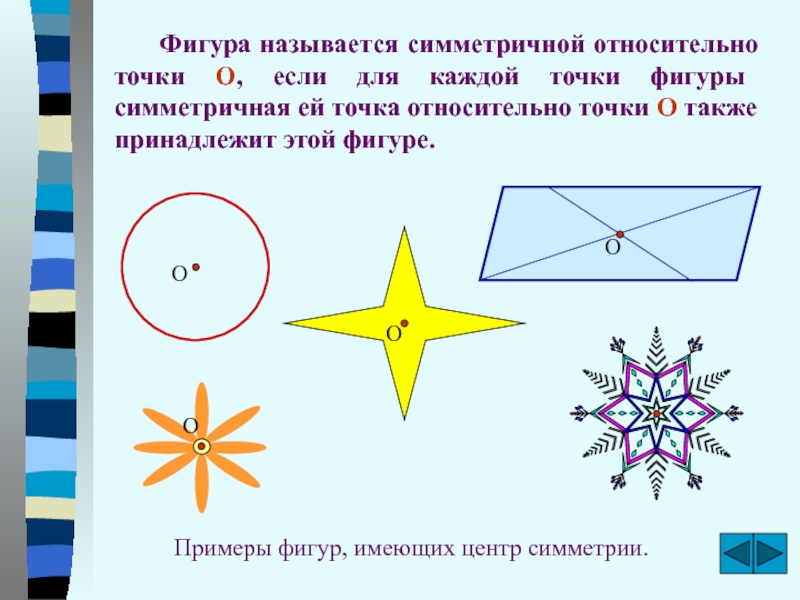
Слайд 10 Фигура называется симметричной относительно точки О, если
для каждой точки фигуры симметричная ей точка относительно точки О
также принадлежит этой фигуре. Примеры фигур, имеющих центр симметрии.
Слайд 11Осевая симметрия
Две точки А и А1 называются симметричными
относительно прямой n, если эта прямая проходит через середину отрезка
АА1 и перпендикулярна к нему.n
А
А1
n – ось симметрии
О
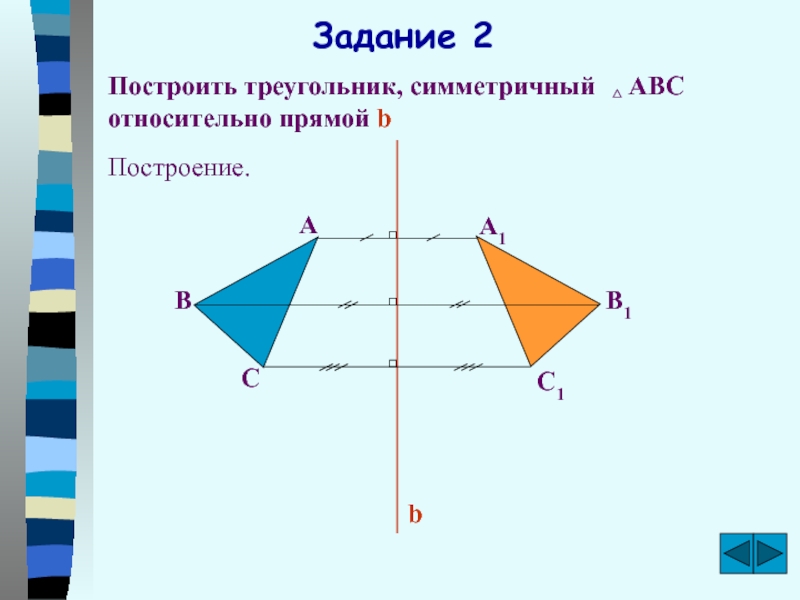
Слайд 13
b
С
В
А
А1
В1
С1
Задание 2
Построить треугольник, симметричный АВС относительно прямой b
Построение.
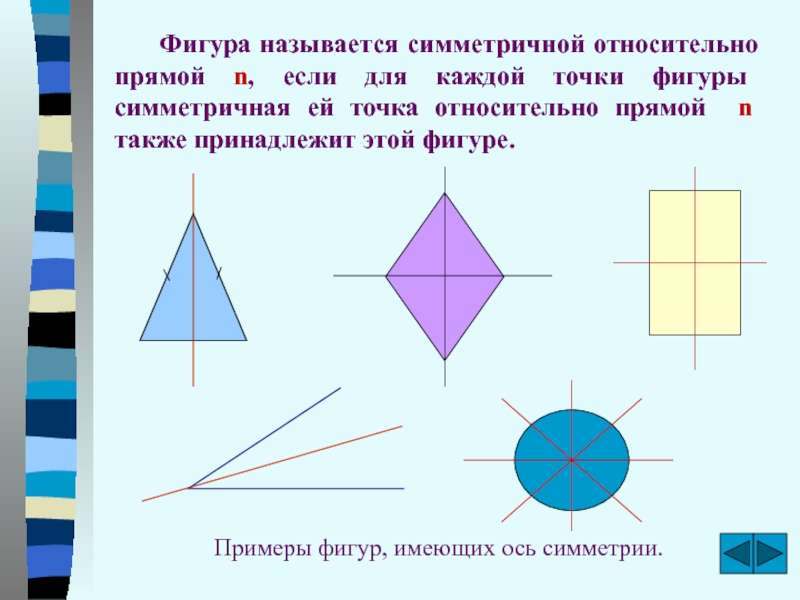
Слайд 14 Фигура называется симметричной относительно прямой n, если
для каждой точки фигуры симметричная ей точка относительно прямой n
также принадлежит этой фигуре. Примеры фигур, имеющих ось симметрии.