Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многоугольники
Содержание
- 1. Правильные многоугольники
- 2. Работу выполнила учитель математикиМОУ «Гимназия №11»Лисицына Е.Ф.
- 3. Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны
- 4. Известно, что сумма всех внутренних углов выпуклого n-угольника равна (n-2)·180ºα=60ºα=90ºα=n - 2 n·180ºα=108ºα=120º180º360º540º720º
- 5. Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают.
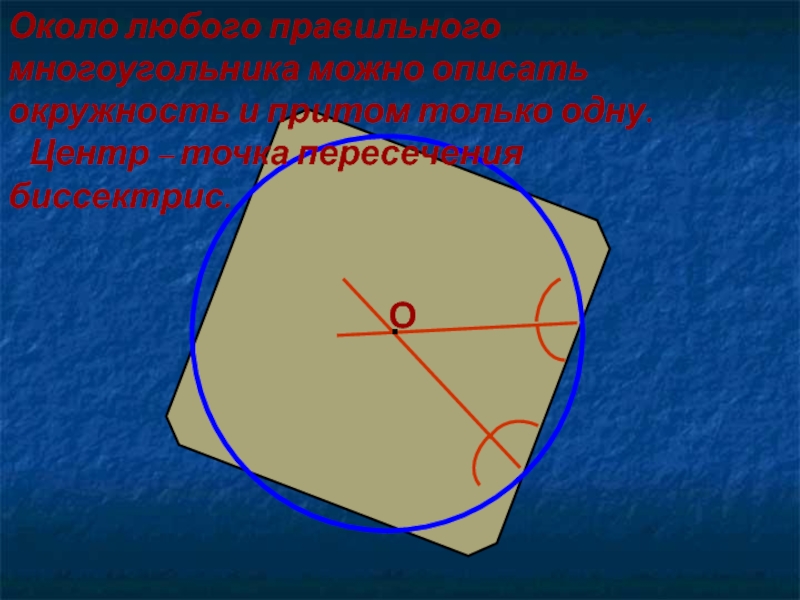
- 6. Около любого правильного многоугольника можно описать окружность
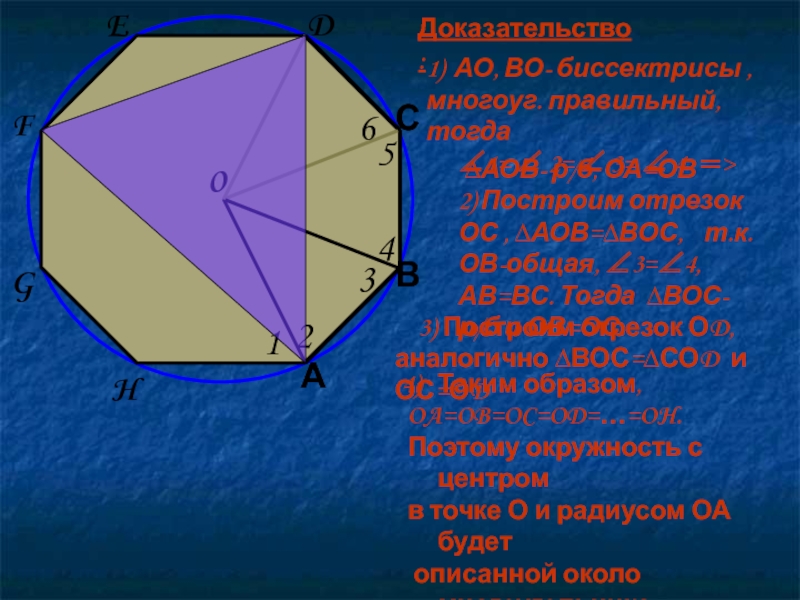
- 7. o1234561) АО, ВО- биссектрисы ,многоуг. правильный, тогда
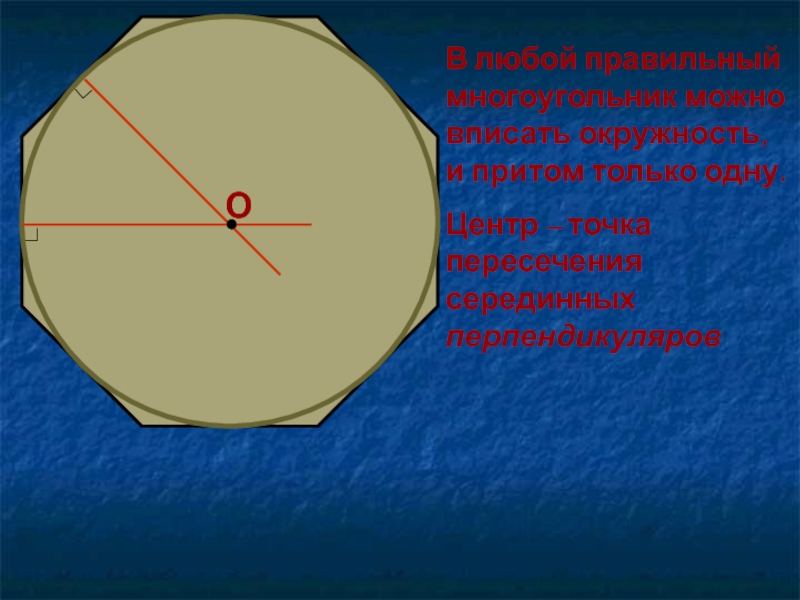
- 8. В любой правильный многоугольник можно вписать окружность,
- 9. •∟∟Доказательство:ABCDEFGK∟О-центр описанной
- 10. Простейшее построение правильного четырехугольникаПостроение правильного восьмиуголь- ника
- 11. Построение правильных многоугольников, то есть деление окружности
- 12. Именно в школе ПИФАГОРА зародилось учение о
- 13. По некоторым источникам, он являлся автором сочинения
- 14. Описал построение правильных 3 , 4 , 5 , 6- угольников, построил правильный 15-угольник
- 15. Развитие готического стиля и широкое применение витражей
- 16. Именно Альбрехт Дюрер осуществил новое построение
- 17. Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;Решил задачу построения правильного восьмиугольника;Разработал принципы черчения художественно исполненных букв.
- 18. Для своего друга Луки Пачоли Леонардо, глубоко
- 19. математик Иоганн Кеплер создал трактат «Новогодний подарок
- 20. Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил заняться математикой, а не филологией.
- 21. ЗАКЛЮЧЕНИЕ ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ ДОСТОЙНЫ И ВАШЕГО
- 22. Скачать презентанцию
Работу выполнила учитель математикиМОУ «Гимназия №11»Лисицына Е.Ф.
Слайды и текст этой презентации
Слайд 4Известно, что сумма всех внутренних углов выпуклого n-угольника равна
(n-2)·180º
α=60º
α=90º
α=
n - 2
n
·180º
α=108º
α=120º
180º
360º
540º
720º
Слайд 5Правильный многоугольник является вписанным в окружность и описанным около окружности,
причем центры этих окружностей совпадают.
Слайд 6
Около любого правильного многоугольника можно описать окружность и притом только
одну.
Центр – точка пересечения биссектрис.
·
О
Слайд 7
o
1
2
3
4
5
6
1) АО, ВО- биссектрисы ,
многоуг. правильный, тогда
∠1= ∠ 2= ∠ 3= ∠ 4 ═>
∆АОВ- р/б, ОА=ОВ
2) Построим отрезок ОС , ∆АОВ=∆ВОС, т.к. ОВ-общая, ∠3=∠4, АВ=ВС. Тогда ∆ВОС- р/б и ОВ=ОС.
А
В
С
D
3) Построим отрезок ОD, аналогично ∆ВОС=∆СОD и ОС=ОD
E
F
G
H
Таким образом,
OA=OB=OC=OD=…=OH.
Поэтому окружность с центром
в точке О и радиусом ОА будет
описанной около многоугольника.
Доказательство:
Слайд 8
В любой правильный многоугольник можно вписать окружность, и притом только
одну.
Центр – точка пересечения серединных перпендикуляров
•
О
∟
∟
Слайд 9
•
∟
∟
Доказательство:
A
B
C
D
E
F
G
K
∟
О-центр описанной
окружности;
Построим ОА,ОВ,ОС,OD
∆AOB, ∆BOC, ∆COD-р/б,
OH1,
OH2, OH3-высоты и медианы. 2) ∆AOB=∆BOC=∆COD ═> OH1=OH2=OH3.
3) Окружность с центром в точке О и радиусом OH1 будет вписанной в этот многоугольник, т.к. касается всех его сторон.
H1
H2
H3
O
Слайд 11Построение правильных многоугольников, то есть деление окружности на равные части,
позволяло решать практические задачи:
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных
театров;4)Создание астрономических сооружений
Слайд 12Именно в школе ПИФАГОРА зародилось учение о правильных многоугольниках; кроме
того, пифагорейцы рассмотрели вопрос покрытия плоскости правильными многоугольниками.
Слайд 13По некоторым источникам, он являлся автором сочинения о правильных многоугольниках,
часто присоединяемого к "Началам" в качестве XV книги. Исидор из
Милета (532-537 гг.) - византийский архитектор и геометр, построивший вместе с Анфи - мием собор Святой Софии в Константинополе.
Слайд 15Развитие готического стиля и широкое применение витражей в строительстве соборов
также заставило вернуться к задачам построения правильных многоугольников.
Слайд 16 Именно Альбрехт Дюрер осуществил новое построение правильного пятиугольника, передав
потомкам средневековый способ построения постоянным раствором циркуля.
Слайд 17Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;
Решил задачу построения правильного
восьмиугольника;
Разработал принципы черчения художественно исполненных букв.
Слайд 18Для своего друга Луки Пачоли Леонардо, глубоко интересующийся пропорциями, создал
иллюстрации многогранников, гранями которых являются правильные многоугольники.
Слайд 19математик Иоганн Кеплер создал трактат «Новогодний подарок или о шестиугольных
снежинках», опубликованный в 1611 году. В нем он практически привел
первый пример разбиения плоскости на правильные шестиугольники.
Слайд 20Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил
заняться математикой, а не филологией.
Слайд 21ЗАКЛЮЧЕНИЕ
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ ДОСТОЙНЫ И ВАШЕГО ПРИСТАЛЬНОГО ВНИМАНИЯ.
ВОЗМОЖНО,ИМЕННО
ВЫ СОВЕРШИТЕ НОВЫЕ ОТКРЫТИЯ.
ЖЕЛАЮ УСПЕХА!
