Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение основных свойств площадей к решению задач 9 класс
Содержание
- 1. Применение основных свойств площадей к решению задач 9 класс
- 2. Необходимость в понятии «площадь» возникла из жизненных
- 3. Историческая справка.Вопросом о вычислении площади люди интересовались
- 4. Площадь простой фигуры это положительная величина, численное
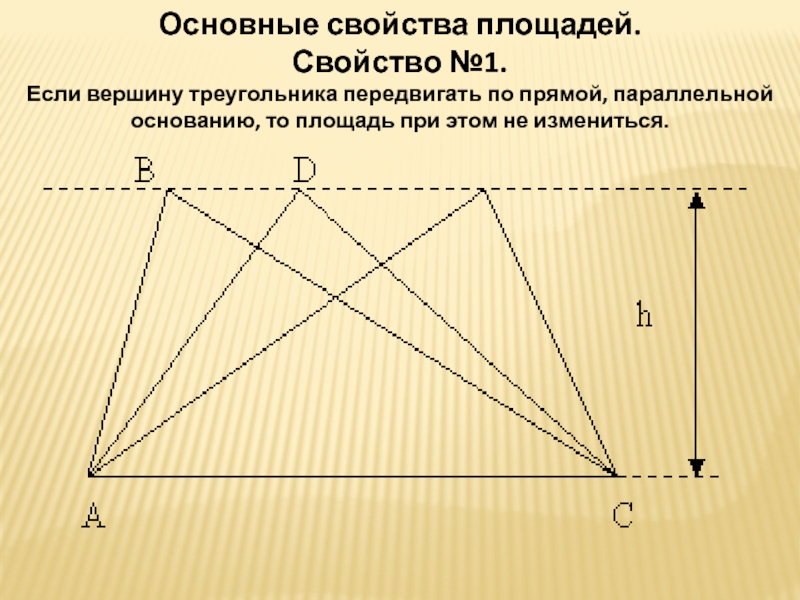
- 5. Основные свойства площадей.Свойство №1.Если вершину треугольника передвигать
- 6. Свойство №2.Если два треугольника имеют одинаковые высоты,
- 7. Свойство №3.Если два треугольника имеют общий угол,
- 8. Свойство №4.Отношение площадей подобных треугольников равны квадрату коэффициента подобия.
- 9. Свойство № 5.Медиана треугольника делит его на две равновеликие части.
- 10. Свойство №6.Медианы треугольника делят его на три равновеликие части.
- 11. Свойство №7.Средние линии треугольника площади S отсекают от него треугольники площади 1/4 S
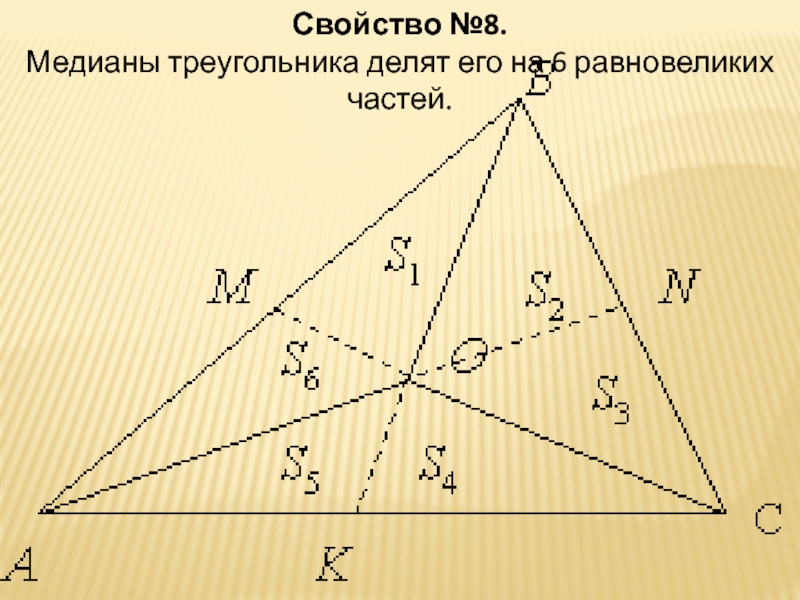
- 12. Свойство №8.Медианы треугольника делят его на 6 равновеликих частей.
- 13. Тест.
- 14. Применение основных свойств к решению задач.Задача №1.На
- 15. Задача №2.Точки M и N расположены на стороне BC треугольника ABC, а точка K – на
- 16. Задача №3.Равнобедренный треугольник ABC с основанием BC
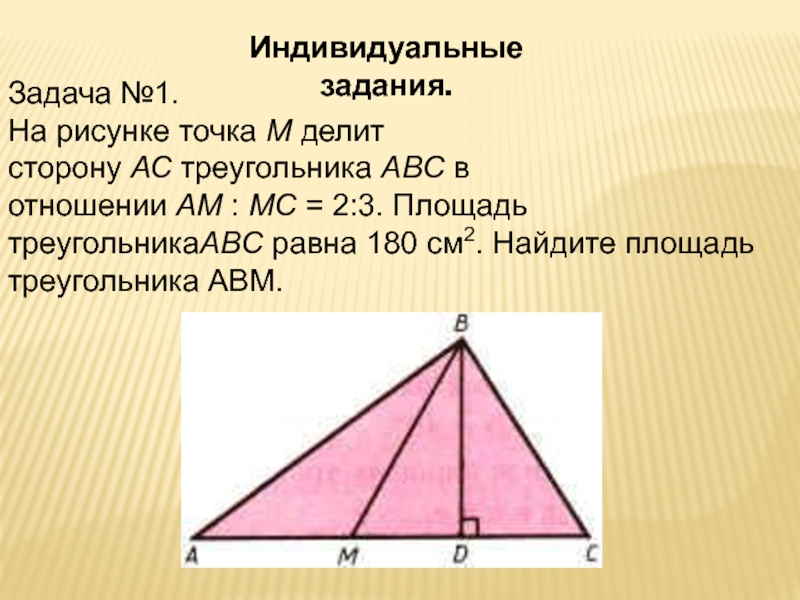
- 17. Индивидуальные задания.Задача №1.На рисунке точка М делит сторону АС треугольника ABC в отношении AM : МС = 2:3. Площадь треугольникаABC равна 180 см2. Найдите площадь треугольника AВM.
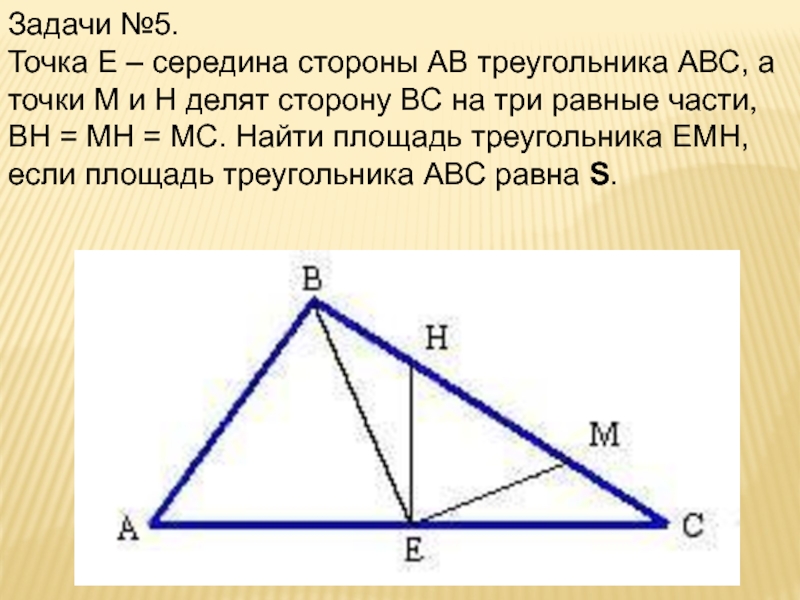
- 18. Задачи №5.Точка Е – середина стороны АВ
- 19. Задачи с разбором решения.№1
- 20. №2№3
- 21. Вывод: Решение задач на вычисление площадей нельзя
- 22. Самостоятельная работа по группам.Задача №1Вершина A в
- 23. Д/З: Тест 25 №21,23.
- 24. Скачать презентанцию
Необходимость в понятии «площадь» возникла из жизненных потребностей. В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе. Позже возникла потребность в измерении и сравнении разнообразных
Слайды и текст этой презентации
Слайд 1Открытый урок по теме: «Применение основных свойств площадей к решению
задач».
Нина Фёдоровна.Слайд 2Необходимость в понятии «площадь» возникла из жизненных потребностей. В древности
люди использовали для измерения длин те измерительные приборы, которые всегда
были при себе. Позже возникла потребность в измерении и сравнении разнообразных «фигур» . Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.Слайд 3Историческая справка.
Вопросом о вычислении площади люди интересовались ещё с древнейших
времён. Наиболее известная задача - это задача Дидона.
Финикийская царица Дидона
спасалась от своего брата, тирана Пигмалиона. Она отплыла из города Тира в 825 г до н.э. После долгого путешествия корабль пристал к берегам Африки. Дидоне понравилась земля. Она обратилась к местному предводителю Ярбу с просьбой продать кусок земли. Ярб заломил баснословную цену за клочок земли, который можно окружить бычьей шкурой. Но Дедона не растерялась и согласилась. Она расплатилась и отправилась отмерять землю. Сначала она разрезала шкуру так, что получился тонкий кожаный ремешок. Этим ремешком она окружила солидный участок земли, на котором в последствии обосновала великий город Карфаген. Ярб был в ярости, т.к. его одурачили, но он был честным человеком и сдержал слово. Так гласит легенда, но карфагенская цитадель называлась Бирса, что значит «бычья шкура».Слайд 4Площадь простой фигуры это положительная величина, численное значение которой обладает
следующими свойствами:
равные фигуры имеют равные площади;
если фигура разбивается на части,
являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей;площадь квадрата со стороной равной единице измерения, равна 1;
фигуры, имеющие равные площади называются равновеликими.
Слайд 5Основные свойства площадей.
Свойство №1.
Если вершину треугольника передвигать по прямой, параллельной
основанию, то площадь при этом не измениться.
Слайд 6Свойство №2.
Если два треугольника имеют одинаковые высоты, то отношение их
площадей равно отношению длин оснований (сторон, на которые опущены эти
высоты).Слайд 7Свойство №3.
Если два треугольника имеют общий
угол, то их площади относятся
как произведение сторон, заключающих
этот угол.
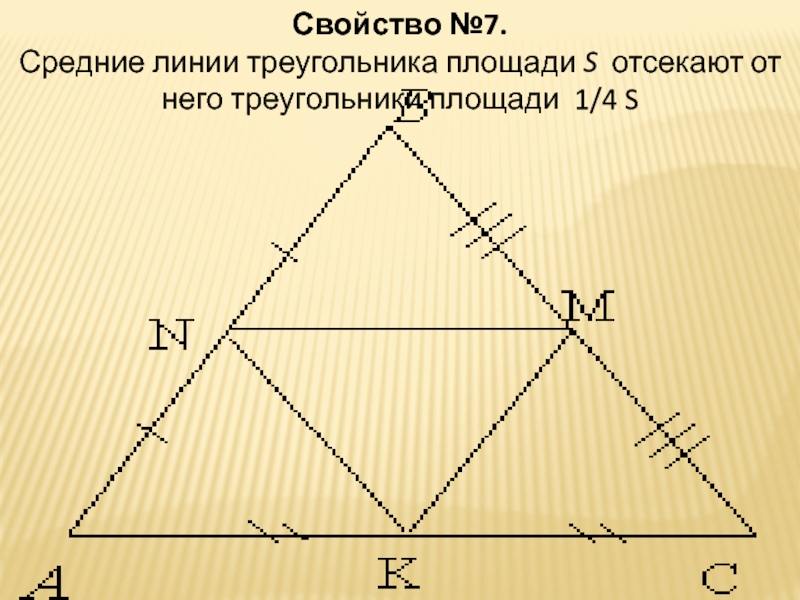
Слайд 11Свойство №7.
Средние линии треугольника площади S отсекают от него треугольники площади
1/4 S
Слайд 14Применение основных свойств к решению задач.
Задача №1.
На сторонах AB и AC треугольника ABC, площадь которого
равна 36 см2, взяты соответственно точки M и K так, что AM/MB = 1/3, а AK/KC = 2/1.
Найдите площадь треугольника AMK.Проведите BK.
Слайд 15Задача №2.
Точки M и N расположены на стороне BC треугольника ABC, а точка K – на стороне AC, причём BM : MN : NC = 1
: 1 : 2 и CK : AK= 1 : 4. Известно, что
площадь треугольника ABC равна 1. Найдите площадь четырёхугольника AMNK.Слайд 16Задача №3.
Равнобедренный треугольник ABC с основанием BC вписан в окружность
с центром O. Площадь треугольника ABC равна
, угол А=45°. Прямая, проходящая через точку О и середину АС, пересекает сторону ВА в точке М. Найдите площадь треугольника ВСМ.Слайд 17Индивидуальные задания.
Задача №1.
На рисунке точка М делит сторону АС треугольника ABC в отношении AM : МС = 2:3. Площадь треугольникаABC равна
180 см2. Найдите площадь треугольника AВM.
Слайд 18Задачи №5.
Точка Е – середина стороны АВ треугольника АВС, а
точки М и Н делят сторону ВС на три равные
части, ВН = МН = МС. Найти площадь треугольника ЕМН, если площадь треугольника АВС равна S.Слайд 21Вывод: Решение задач на вычисление площадей нельзя ограничить только задачами
на применение «основных свойств площадей». При изучении темы вычисления площадей
необходимо использовать широкий круг знаний свойств геометрических фигур.Слайд 22Самостоятельная работа по группам.
Задача №1
Вершина A в параллелограмме ABCD соединена
с точкой P на стороне BC. Отрезок AP пересекает диагональ
BD в точке М. Площадь треугольника АВМ равна 20, а площадь треугольника ВМР равна 16. Найдите площадь параллелограмма АВСD.Задача №2.
Вершина С параллелограмма АВСD соединена с точкой N на стороне AB. Отрезок СN пересекает диагональ BD в точке P. Площадь треугольника BNP равна 8, а площадь треугольника BCP равна 12. Найдите площадь параллелограмма ABCD.