Слайд 1Решение задач на комбинации призмы, шара и пирамиды.
Слайд 2Шар, вписанный в пирамиду
В любую треугольную пирамиду можно вписать шар;
В
пирамиду, у которой в основание можно вписать окружность; центр, которой
служит основанием высоты пирамиды, можно вписать шар;
В любую правильную пирамиду можно вписать шар;
Центр шара, вписанного в пирамиду есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и её проекцией на основание;
Центр сферы (шара), вписанного в правильную пирамиду, лежит на высоте этой пирамиды.
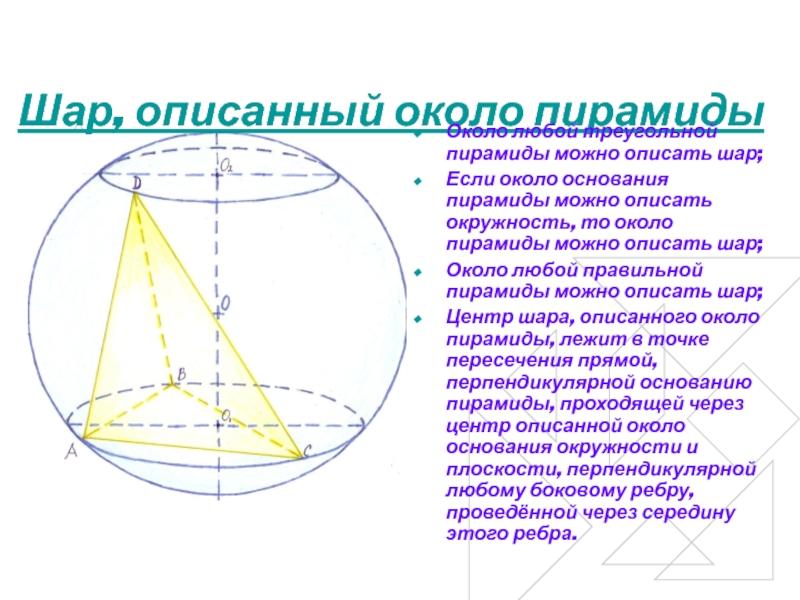
Слайд 3Шар, описанный около пирамиды
Около любой треугольной пирамиды можно описать шар;
Если
около основания пирамиды можно описать окружность, то около пирамиды можно
описать шар;
Около любой правильной пирамиды можно описать шар;
Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра.
Слайд 4
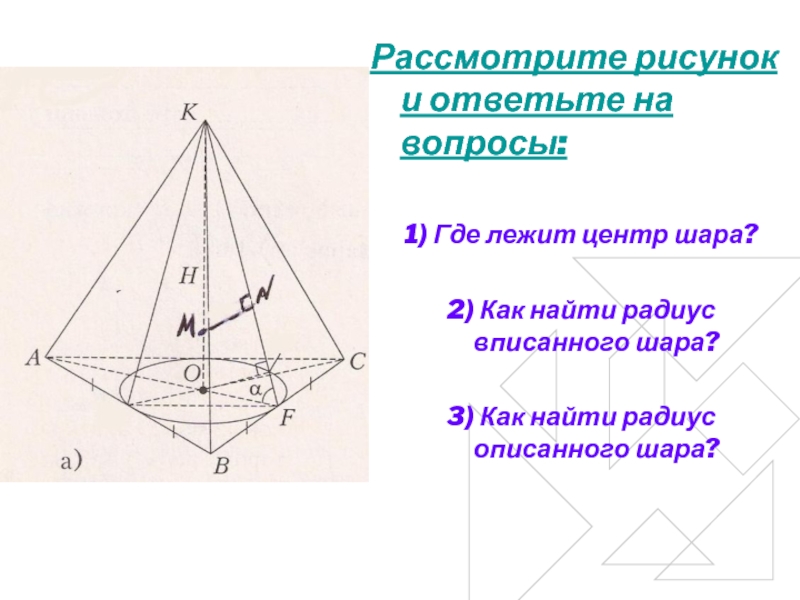
Рассмотрите рисунок и ответьте на вопросы:
1) Где лежит центр шара?
2)
Как найти радиус вписанного шара?
3) Как найти радиус описанного шара?
Слайд 5Рассмотрите рисунки и вставьте пропущенные слова:
Центр шара, вписанного в правильную
треугольную пирамиду, лежит на ______ КО пирамиды и биссектрисы угла
KFO, составленного ______ и её______. Треугольник KNM ______ треугольнику FKO, так как ________ NM/ KM = = FO/FK; r_______, где FO – радиус окружности, вписанной в основание пирамиды.
Слайд 6
Около любой треугольной пирамиды можно описать шар. Центр
шара лежит на высоте пирамиды в точке пересечения
с перпендикуляром, _____ через ______ бокового ребра.
Треугольники КМО и КСО1_______, так как _______ . КО1 ______ пирамиды.
ОО1= КО1– КО=______.
В треугольнике СОО1 по теореме Пифагора СО=___________.
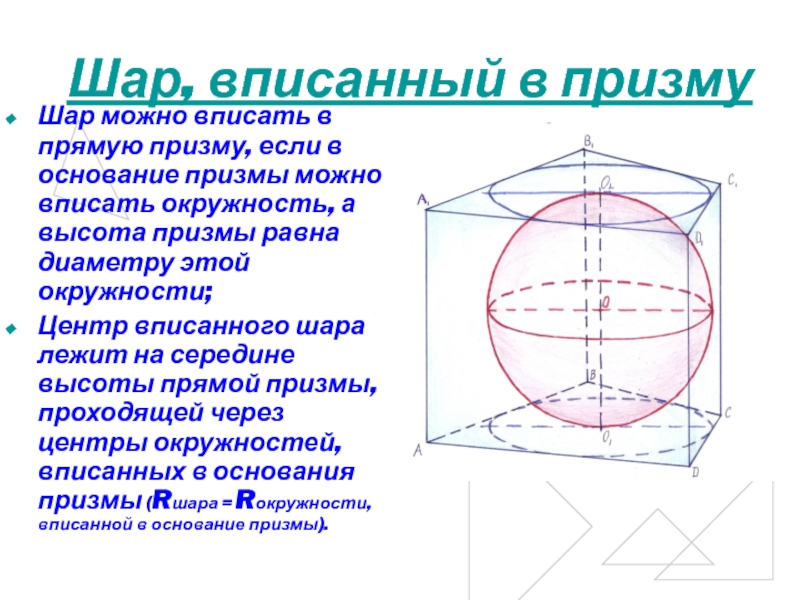
Слайд 7Шар, вписанный в призму
Шар можно вписать в прямую призму, если
в основание призмы можно вписать окружность, а высота призмы равна
диаметру этой окружности;
Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей, вписанных в основания призмы (Rшара = Rокружности, вписанной в основание призмы).
Слайд 8Шар, описанный около призмы
Около призмы можно описать шар, тогда и
только тогда, когда призма прямая и около основания можно описать
окружность;
Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведённой через центр окружности, описанной около основания.
Слайд 9
Решите задачу №1.
В четырёхугольную призму
ABCDA1B1C1D1 , вписана сфера. Площади граней ABB1A1 и CDD1C1 соответственно
равны 6см и 5 см. Найдите площадь боковой поверхности призмы.
Решите задачу №2.
Сфера описана около четырёхугольной призмы ABCDA1B1C1D1. Двугранные углы при рёбрах AA1 и BB1 сооттветственно равны 60º и 95º. Найдите величины двугранных углов при рёбрах CC1 и DD1.
Слайд 10Тест по теме:
«Вписанные и описанные многогранники».
В а р и а
н т 1
Уровень А
1. Нельзя описать шар около…
1) куба;
2) прямоугольного параллелепипеда;
3) прямого параллелепипеда.
2. Можно описать шар около пирамиды, основанием которой является…
1) тупоугольный треугольник;
2) ромб;
3) прямоугольная трапеция.
3. Центр вписанного шара равноудалён…
1) от вершин многогранника;
2) рёбер многогранника;
3) граней многогранника.
4. Нельзя вписать шар в пирамиду, у которой равны…
1) углы между боковыми рёбрами и высотой пирамиды;
2) апофемы;
3) двугранные углы при рёбрах основания.
Слайд 11
5. Нельзя вписать шар в пирамиду, основанием которой является…
1) ромб;
2) прямоугольник;
3) квадрат.
6. Можно вписать
шар в пирамиду, у которой равны…
1) двугранные углы при рёбрах основания;
2) боковые рёбра;
3) углы между боковыми рёбрами и высотой пирамиды.
7. В прямую треугольную призму вписан шар. Тогда высота призмы не может быть равна…
1) диаметру вписанной в основание окружности;
2) диаметру шара;
3) радиусу шара.
8. DABC – правильная пирамида. Q – центр вписанного
шара. Тогда радиус шара – отрезок…
1) QM;
2) QL;
3) QK.
Слайд 12
9. Объём многогранника, описанного около шара радиуса r, равен…
1) V= 1/3r*Sполн;
2) V= 3r*Sполн;
3) V=
Sполн/3r/
Уровень В
1. Ребро куба равно 6 см. Тогда радиус вписанного в куб шара равен…
2. Радиус описанного около куба шара равен 2√3 см. Тогда ребро куба равно …
3. В правильную треугольную призму
вписана сфера, радиус которой равен √2 см.
Тогда расстояние от центра сферы до
ребра основания равно…
Слайд 13
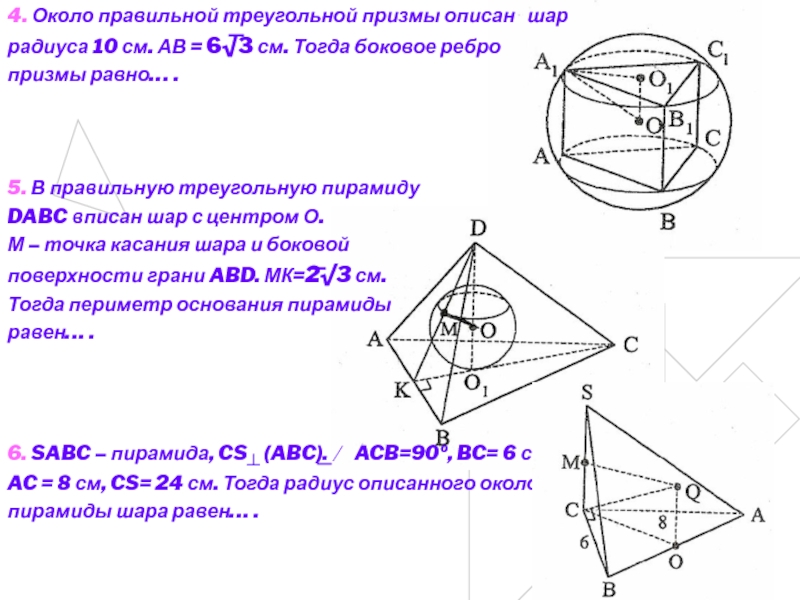
4. Около правильной треугольной призмы описан шар
радиуса 10 см.
АВ = 6√3 см. Тогда боковое ребро
призмы равно… .
5. В правильную треугольную пирамиду
DABC вписан шар с центром О.
М – точка касания шара и боковой
поверхности грани ABD. МК=2√3 см.
Тогда периметр основания пирамиды
равен… .
6. SABC – пирамида, CS┴ (ABC). ⁄ ACB=90º, BC= 6 см,
AC = 8 см, CS= 24 см. Тогда радиус описанного около
пирамиды шара равен… .
Слайд 14
В а р и а н т 2.
Уровень А
1.
Можно описать шар около…
1)
прямоугольного параллелепипеда;
2) прямого параллелепипеда;
3) наклонного параллелепипеда.
2. Нельзя описать шар около пирамиды, основанием которой является…
1) тупоугольный треугольник;
2) ромб;
3) равнобедренная трапеция.
3. Центр описанного шара равноудалён от…
1) вершин многогранника;
2) рёбер многогранника;
3) граней многогранника.
4. Нельзя не описать шар около пирамиды, у которой равны…
1) двугранные углы при рёбрах основания;
2) апофемы;
3) боковые рёбра.
Слайд 15
5. Можно вписать шар в пирамиду, основанием которой является…
1) ромб;
2) прямоугольник;
3) параллелограмм.
6. Нельзя вписать
шар в пирамиду, у которой равны…
1) углы наклона боковых рёбер;
2) апофемы;
3) двугранные углы при рёбрах основания.
7. В прямую треугольную призму вписан шар. Тогда высота призмы…
1) равна радиусу шара;
2) в два раза больше радиуса;
3) в два раза меньше радиуса.
8. DABC – правильная пирамида. Q – центр описанного
шара. Тогда радиус шара – отрезок…
1) QM;
2) QC;
3) QL.
Слайд 16
9. Многогранник описан около шара. Тогда радиус шара равен…
1) r= 3V/SПОЛН;
2) r= 3Sполн/V;
3) r=
V/ Sполн.
Уровень В
1. Радиус вписанного в куб шара равен 3 см. Тогда ребро куба равно… .
2. Ребро куба равно 4√3 см. Тогда радиус описанного около куба шара равен… .
3. В правильную треугольную призму вписана
сфера. Расстояние от центра сферы до ребра
основания равно 5√2 см. Тогда радиус сферы
равен… .
Слайд 17
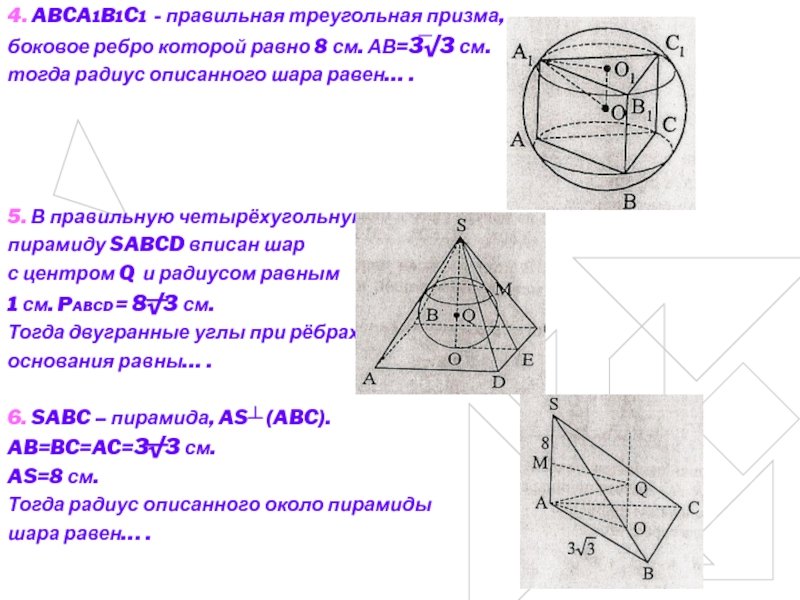
4. ABCA1B1C1 - правильная треугольная призма,
боковое ребро которой равно
8 см. АВ=3√3 см.
тогда радиус описанного шара равен… .
5. В
правильную четырёхугольную
пирамиду SABCD вписан шар
с центром Q и радиусом равным
1 см. PABCD = 8√3 см.
Тогда двугранные углы при рёбрах
основания равны… .
6. SABC – пирамида, AS┴ (ABC).
AB=BC=AC=3√3 см.
AS=8 см.
Тогда радиус описанного около пирамиды
шара равен… .
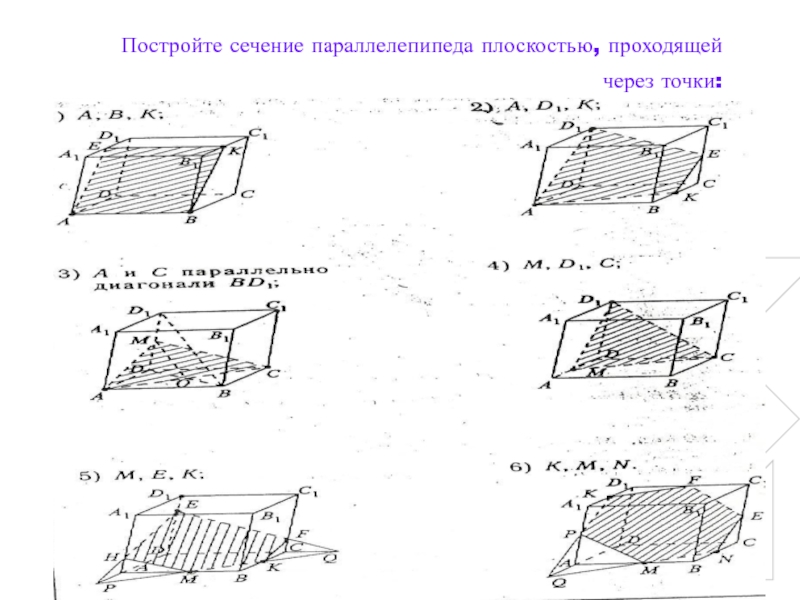
Слайд 18Постройте сечение параллелепипеда плоскостью, проходящей через точки: