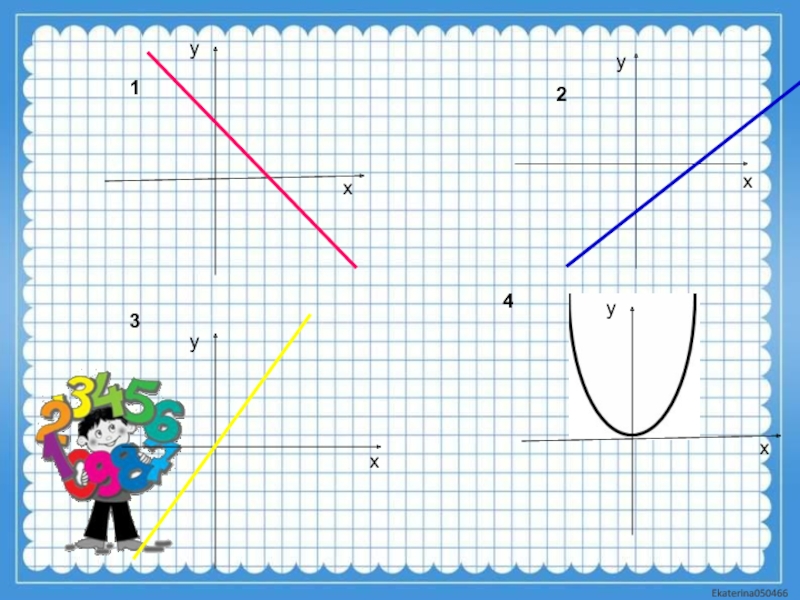
Слайд 1Вероятность равновозможных событий
Слайд 325.4.16
Экспресс - опрос
Какую функцию называют линейной?
Что является графиком линейной
функции?
Какую функцию называют
прямой пропорциональностью?
В каком случае графики двух линейных функций
являются параллельными прямыми?
Сколько точек достаточно для построения прямой?
Слайд 5
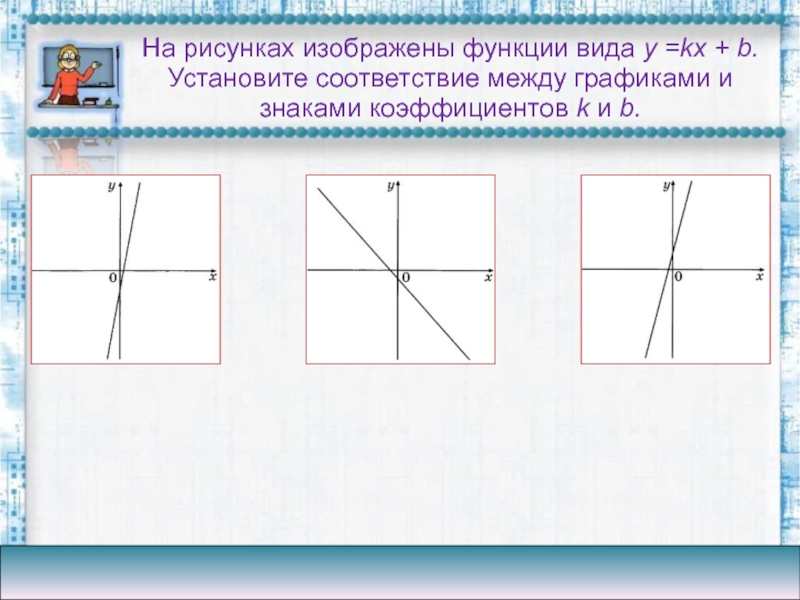
На рисунках изображены функции вида y =kx + b. Установите
соответствие между графиками и знаками коэффициентов k и b.
Слайд 6
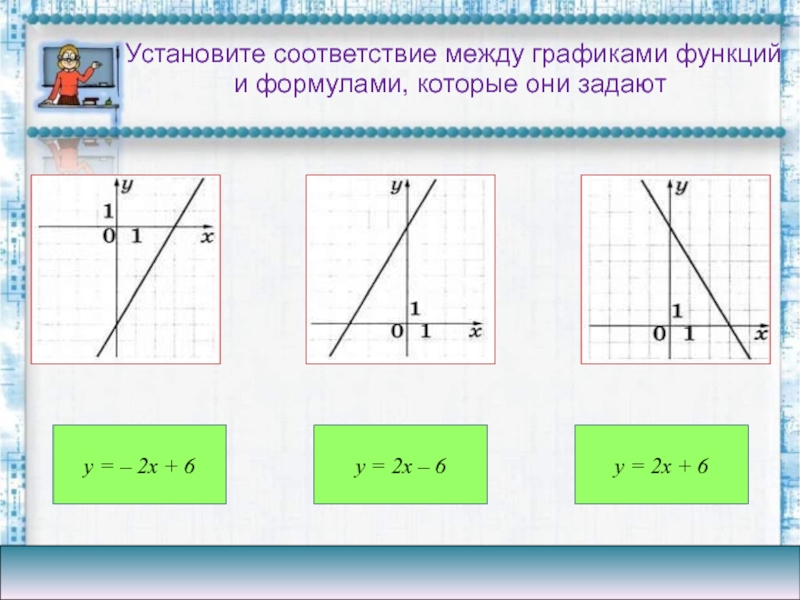
Установите соответствие между графиками функций
и формулами, которые они задают
y
= – 2x + 6
y = 2x – 6
y
= 2x + 6
Слайд 7
Установите соответствие между графиками функций
и формулами, которые они задают
y
= x2 + 2
y = - 2 / x
y =
2x
Слайд 9Статистические характеристики
Среднее арифметическое
ряда чисел
- частное от деления суммы этих чисел на число
слагаемых
Задача: сколько минут тратят на домашнее задание по алгебре?
30, 25, 20, 25, 30
30+25+20+25+30 = 26
5
Слайд 10Статистические характеристики
Размах ряда чисел - разность между наибольшим и
наименьшим из этих чисел
Пример: дан упорядоченный ряд чисел
35, 35, 36,
36, 36, 36, 37, 37, 38, 39, 39
39 – 35 = 4 - размах ряда
Слайд 11Статистические характеристики
Модой ряда чисел – число наиболее часто встречающееся
в данном ряду
Ряд чисел может иметь более одной моды или
не иметь моды совсем
35, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
36 –мода ряда, так как встречается чаще всего в этом ряду
Слайд 12Статистические характеристики
Медианой упорядоченного ряда чисел с нечётным числом членов
называется среднее в ряду число;
с чётным числом членов
среднее арифметическое чисел, записанных посередине
1) 64, 72, 72, 75, 78, 82, 85, 91, 93
2) 64, 72, 72, 75, 78, 82, 85, 88, 91, 93
Слайд 13Домашняя работа
№ 806
а) Витя б) Петя в) 10
г)
41/8≈5,1 д)5,5
1 группа
№ 808
Среднее арифмтическое 42/11=3,8
Мода 4
Медиана 4
2 группа
№ 809
Среднее арифметическое 152 000р
Мода 100 000 р
Медиана 100 000 р
Слайд 14Прочтите текст и ответьте на вопросы: Что изучает теория вероятности?
Где, в
каких областях, имеет применение? Убедил ли вас текст, что теорию вероятности необходимо изучать как и любую другую науку
Математику многие любят за ее вечные истины: дважды два всегда четыре, сумма четных чисел четна, а площадь прямоугольника равна произведению его смежных сторон. В любой задаче, которую мы решаем на уроках математики, у всех получается один и тот же ответ – нужно только не делать ошибок в решении. Реальная жизнь оказывается не такой простой и однозначной.
Исходы многих явлений невозможно предсказать заранее, результат может быть случайным событием. Однако случай тоже имеет свои законы, которые и изучает теория вероятностей.
Теория вероятности имеет большое значение в экономике, медицине, военном деле. Как вы думаете, нужны ли командиру армии законы теории вероятности? На олимпиаде в Сочи во время биатлона вы слышали «Антон Шипулин. Процент попадания на стойке равен 93». Как вы это понимаете? Во время военных учений какому экипажу доверит командир полка поражение цели: с вероятность 0,6 или 0,9? Сейчас теория вероятностей имеет статус точной науки наравне с арифметикой, алгеброй, геометрией, и т.д.Этот раздел математики сейчас входит в школьные учебники и уже включен в программу экзамена.

Слайд 15Вероятность равновозможных событий
Слайд 16любое явление, которое происходит или не происходит
пример: изменение погоды
-
результаты испытаний (опытов), наблюдений и измерений, производимых людьми
пример: измерение температуры воздуха
Слайд 17Событие
случайное достоверное невозможное
то,
которое в данных условиях произойти не может
то, которое в данных
условиях обязательно произойдет
то, которое в данных условиях может произойти, а может не произойти
Слайд 18исходы
Равновозможные Неравновозможныеные
Если шансы этих исходов
одинаковы
Если шансы этих
исходов
не одинаковы
Слайд 19Введем обозначения
Р — вероятность наступления события,
А — событие,
n -
число всех возможных исходов эксперимента,
m - число всех благоприятных
исходов события А:
P (A) =
Слайд 20
Вероятность = число благоприятных исходов
общее число исходов
Задача 1.
Из 100 лампочек 3 бракованные. Какова вероятность купить неисправную лампочку?
Слайд 21Задача 2.
Случайным образом выбирают 1 букву из русского алфавита. Какова
вероятность того, что это будет буква «А»?
Слайд 22Задача 3.
На столе 12 кусков пирога. В трех «счастливых» из
них запечены призы. Какова вероятность взять «счастливый» кусок пирога?
Слайд 23Задача 4
Из 100 лампочек 3 бракованные. Какова вероятность купить
исправную лампочку?
Задача 5.
В ящике лежат 3 красных шара, 9 белых шаров, 10 зелёных и 7 коричневых. Из ящика вынимают 1 шар. Какова вероятность того, что шар окажется цветным (не белым).
Задача из демоварианта - 2016
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Экзамен - 2014 год
В фирме такси в данный момент свободно 10 машин: 5 черных, 3 желтых и 2 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Слайд 27Задача из сборника по подготовке к ОГЭ
Из букв слова ВЕРЕТЕНО
наугад выбирают одну букву. Найдите вероятность того, что будет выбрана
буква Е.
Слайд 28Задача из сборника по подготовке к ОГЭ
Из букв слова ВЕРЕТЕНО
наугад выбирают одну букву. Найдите вероятность того, что будет выбрана
буква Е.
Слайд 29Экзамен — 2015
1) У бабушки 20 чашек: 15 с красными
цветами, остальные с синими. Бабушка наливает чай в случайно выбранную
чашку. Найдите вероятность того, что это будет чашка с синими цветами.
2) В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым
будет стартовать спортсмен из России.
Слайд 31
Нет,
без явно усиленного
трудолюбия,
ни талантов, ни гениев
Д.И. Менделеев.