Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом 10 класс
Содержание
- 1. Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом 10 класс
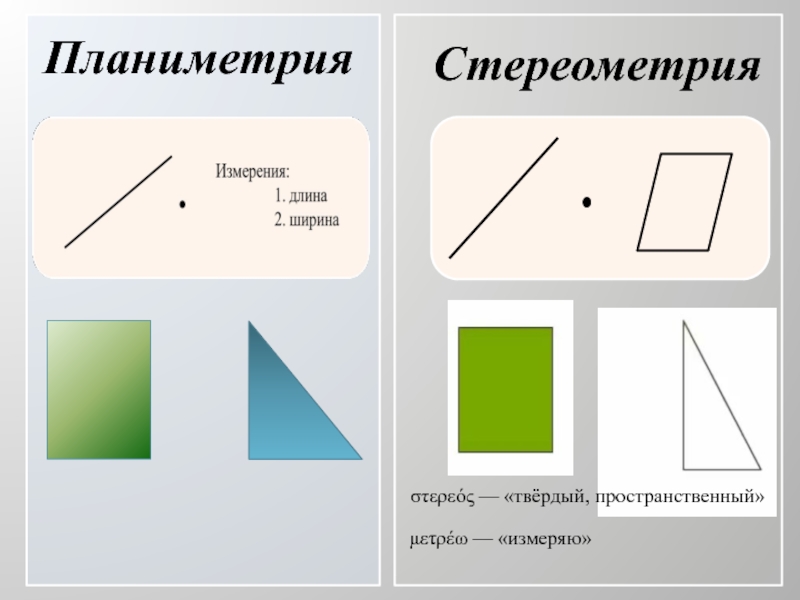
- 2. ПланиметрияСтереометрияστερεός — «твёрдый, пространственный»μετρέω — «измеряю»
- 3. Стереометрия
- 4. Измерения:Длина.Ширина.Высота.Геометрическое тело обладает вместимостью
- 5. Геометрические тела, как и все геометрические фигуры,
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Пифагорейская философская школаVI – V вв. до
- 10. Слайд 10
- 11. Некоторые следствияиз аксиом стереометрии
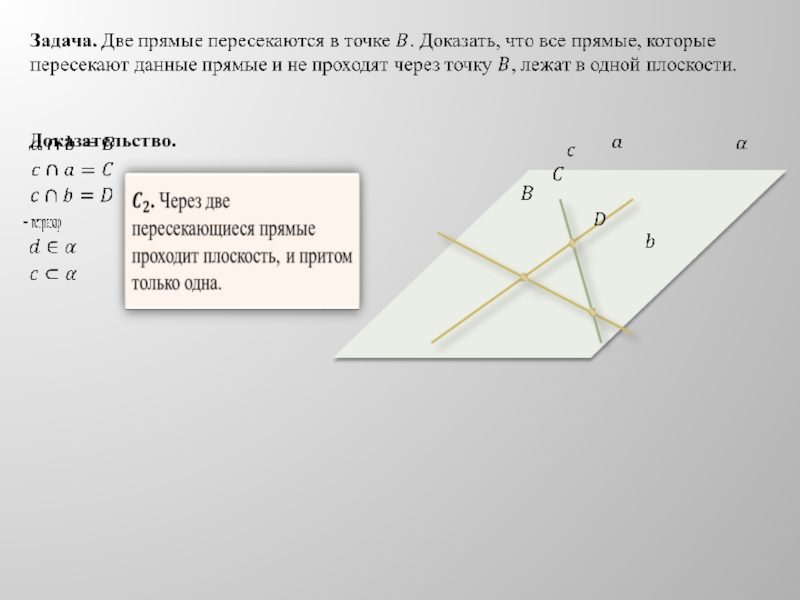
- 12. Доказательство.
- 13. Доказательство.
- 14. Способы задания плоскости Через три точки не
- 15. Решение.
- 16. Доказательство.
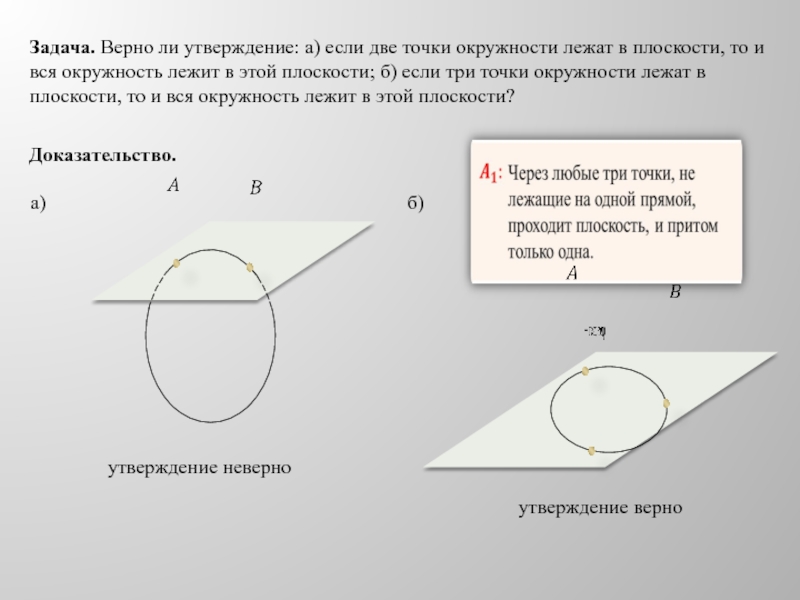
- 17. Задача. Верно ли утверждение: а) если две
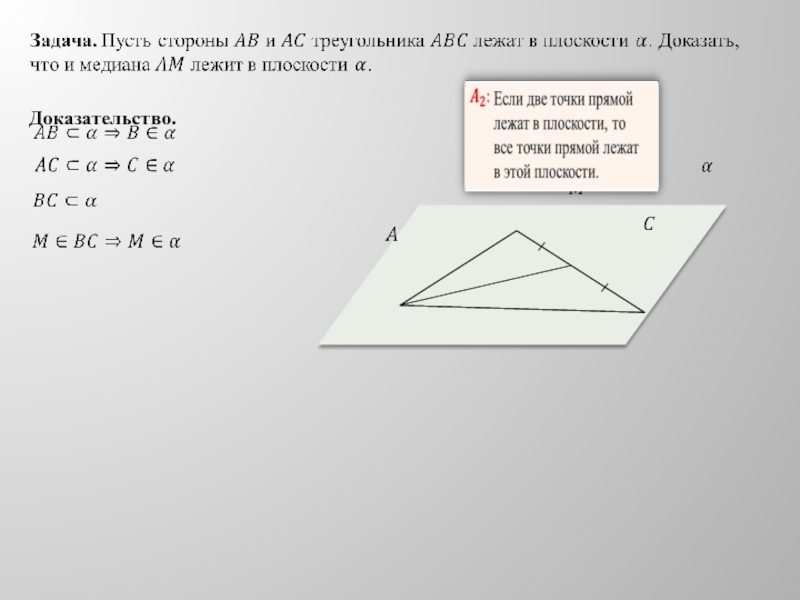
- 18. Доказательство.
- 19. Скачать презентанцию
ПланиметрияСтереометрияστερεός — «твёрдый, пространственный»μετρέω — «измеряю»
Слайды и текст этой презентации
Слайд 5Геометрические тела, как и все геометрические фигуры, являются воображаемыми объектами.
Геометрическое тело – часть пространства, отделенное от остальной части пространства
границей этого тела. Слайд 9Пифагорейская философская школа
VI – V вв. до нашей эры
Пифагор Самосский
570 — 490 гг. до н. э.
Слайд 14Способы задания плоскости
Через три точки не лежащие на одной
прямой.
Через прямую и не лежащую на ней точку
Через две пересекающиеся
прямыеСлайд 17Задача. Верно ли утверждение: а) если две точки окружности лежат
в плоскости, то и вся окружность лежит в этой плоскости;
б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?Доказательство.
а)
б)
утверждение неверно
утверждение верно