Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Загадочный и увлекательный треугольник 8 класс
Содержание
- 1. Загадочный и увлекательный треугольник 8 класс
- 2. Загадка
- 3. Загадка
- 4. Слайд 4
- 5. Неравенство треугольника
- 6. Сумма углов треугольника
- 7. Сумма углов треугольника
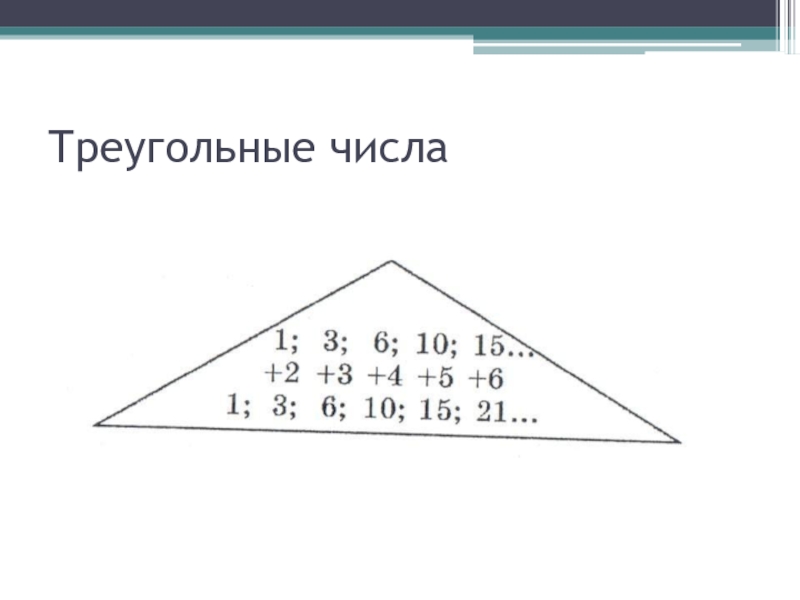
- 8. Треугольные числа
- 9. Виды треугольников
- 10. Криволинейный треугольник
- 11. Слайд 11
- 12. Замечательные дочки-линии и точки
- 13. Замечательные точки
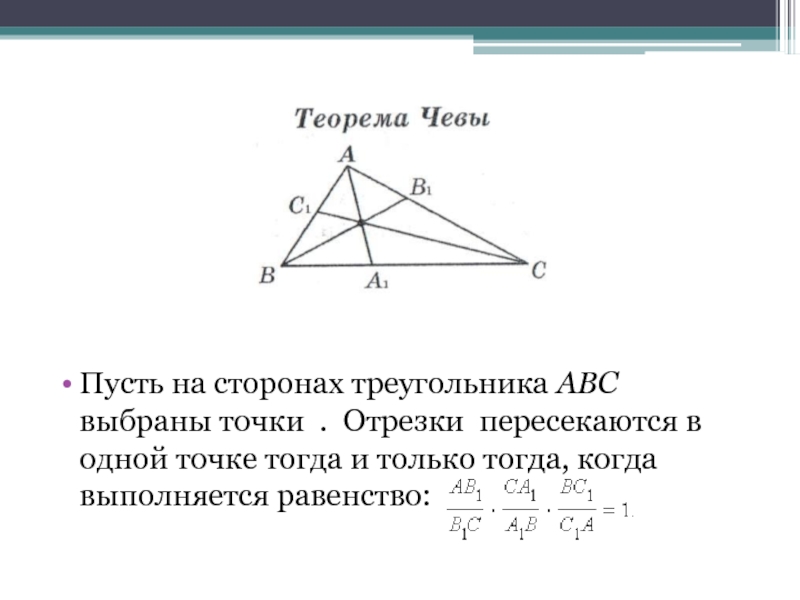
- 14. Пусть на сторонах треугольника ABC выбраны точки
- 15. Теорема утверждает: точки пересечения смежных трисектрис
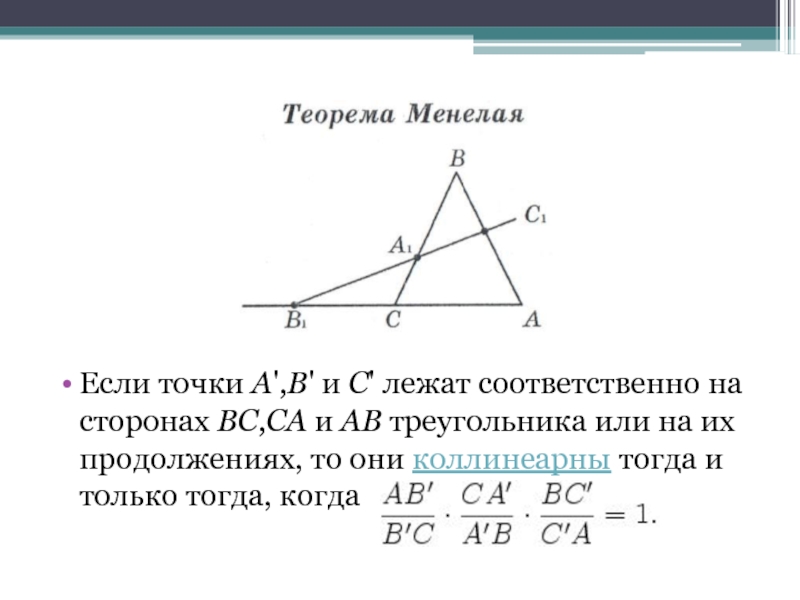
- 16. Если точки A',B' и C' лежат соответственно
- 17. Слайд 17
- 18. Во дворе школы похитили трех друзей. Было
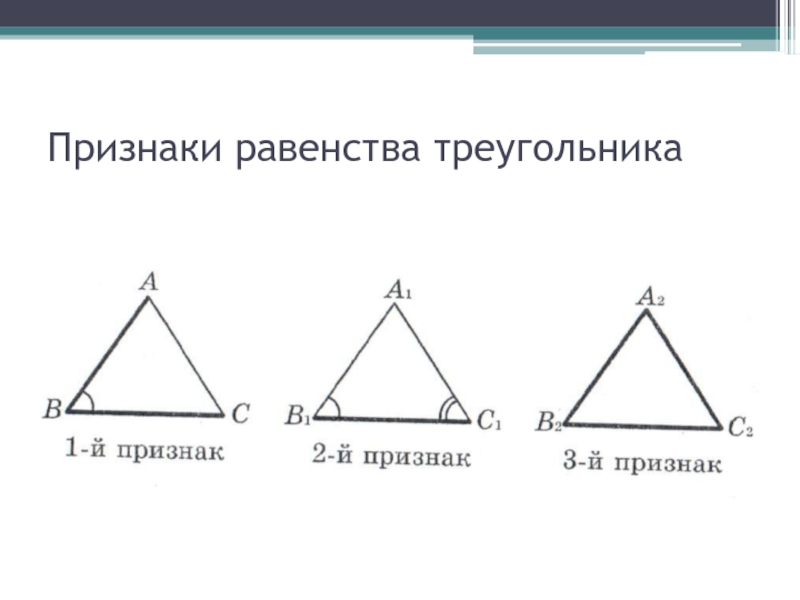
- 19. Признаки равенства треугольника
- 20. ЗадачаЧтобы измерить на местности расстояние между двумя
- 21. Египетский треугольник
- 22. Слайд 22
- 23. Жесткость треугольника
- 24. Теорема Пифагора
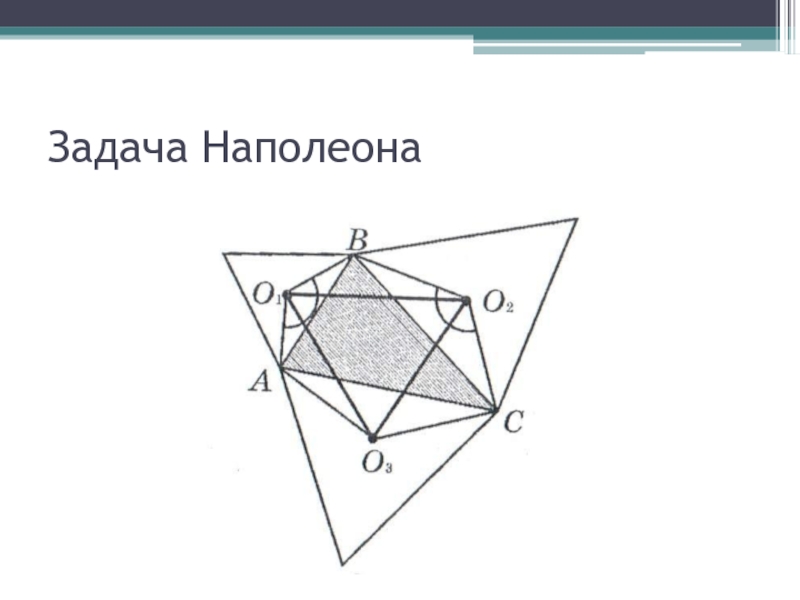
- 25. Задача Наполеона
- 26. Треугольник Паскаля
- 27. Треугольник Паскаля
- 28. Треугольник Паскаля
- 29. Треугольник Паскаля
- 30. Треугольник Паскаля
- 31. Треугольник Паскаля
- 32. Треугольник Паскаля
- 33. Слайд 33
- 34. Слайд 34
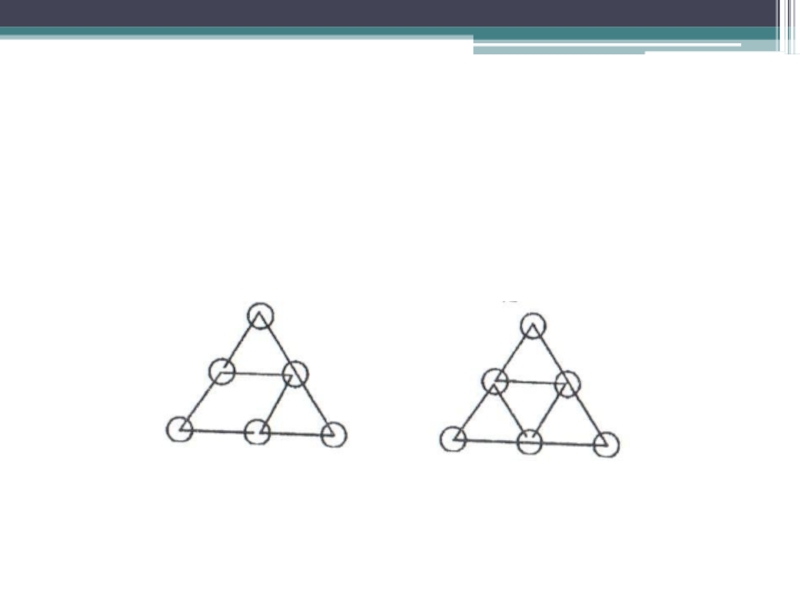
- 35. Соедините кружки одним росчерком
- 36. Слайд 36
- 37. Переложите 4 спички так, чтобы получилось 2 равных треугольника
- 38. Слайд 38
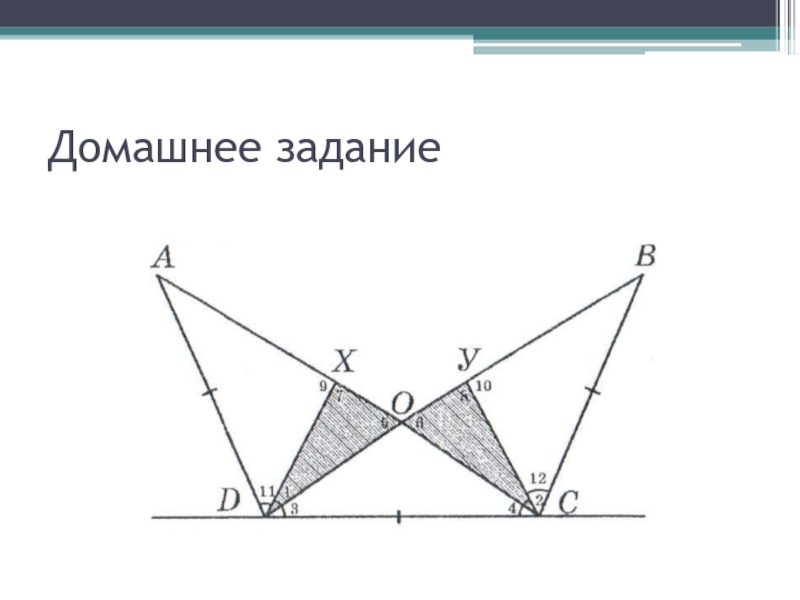
- 39. Домашнее задание
- 40. Домашнее заданиеДано треугольники ∆ADC и ∆DCB –
- 41. Скачать презентанцию
Загадка
Слайды и текст этой презентации
Слайд 1Загадочный и увлекательный треугольник
Собраться вместе – это начало, остаться вместе
– это прогресс, работать вместе – это успех.
трудные дела мы трижды совершим.
Слайд 14
Пусть на сторонах треугольника ABC выбраны точки . Отрезки пересекаются
в одной точке тогда и только тогда, когда выполняется равенство:
Слайд 15
Теорема утверждает:
точки пересечения смежных трисектрис углов произвольного треугольника
точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами
равностороннего треугольника.
Слайд 16
Если точки A',B' и C' лежат соответственно на сторонах BC,CA
и AB треугольника или на их продолжениях, то они коллинеарны
тогда и только тогда, когда
Слайд 18
Во дворе школы похитили трех друзей. Было проведено тщательное расследование,
составлен протокол на 4000 листах, но дело похитили. Учащиеся 7
«г» класса обнаружили в коридоре около двери несколько листов украденного протокола, что позволило нам составить словесный портрет пропавших, и провести собственное расследование.
Слайд 20Задача
Чтобы измерить на местности расстояние между двумя точками А и
В, между которыми нельзя пройти по прямой, выбирают какую-нибудь точку
С, для которой можно измерить расстояния АС и ВС, и откладывают отрезки CD=AC и CE=BC. Тогда расстояние между точками E и D будет равно искомому. Объясните почему.
Слайд 40Домашнее задание
Дано треугольники ∆ADC и ∆DCB – равнобедренные (AC=DC=BC) AC=BD;
DX и DY – биссектрисы углов ADC и DCB.
Доказать ∆DXO=
∆CYO
