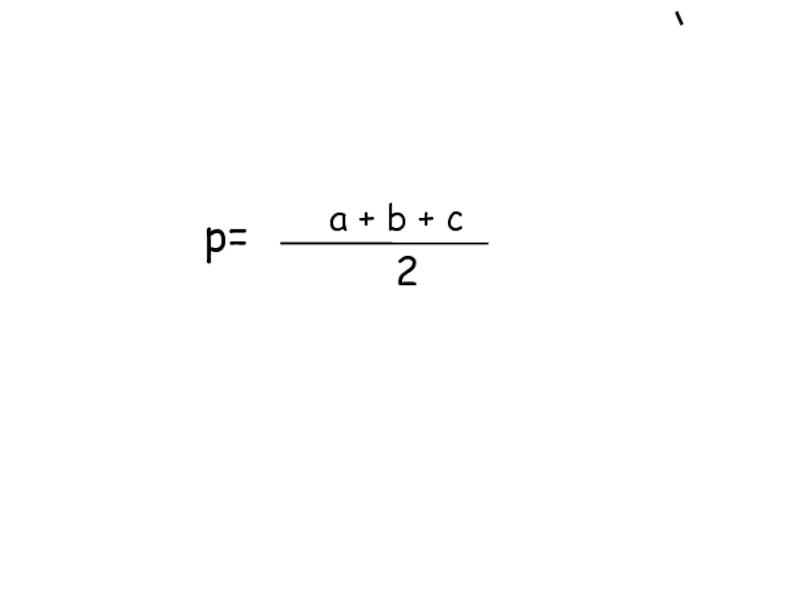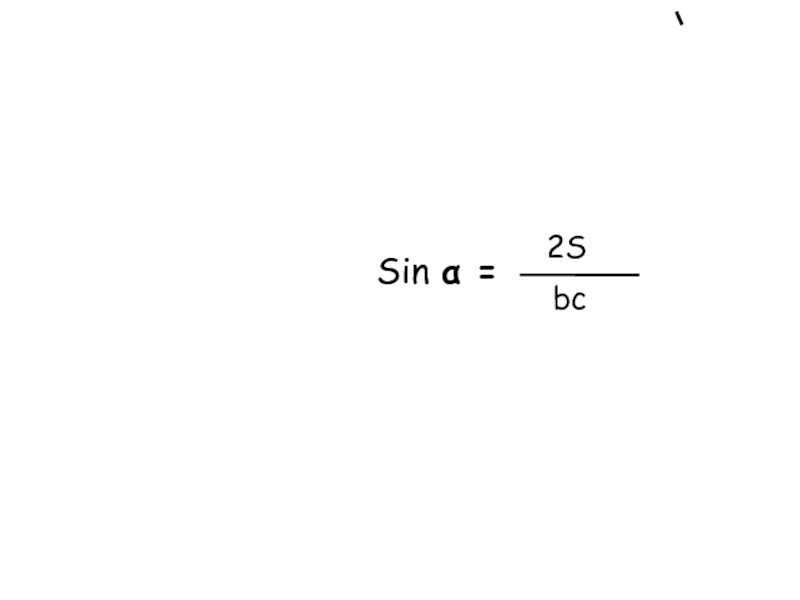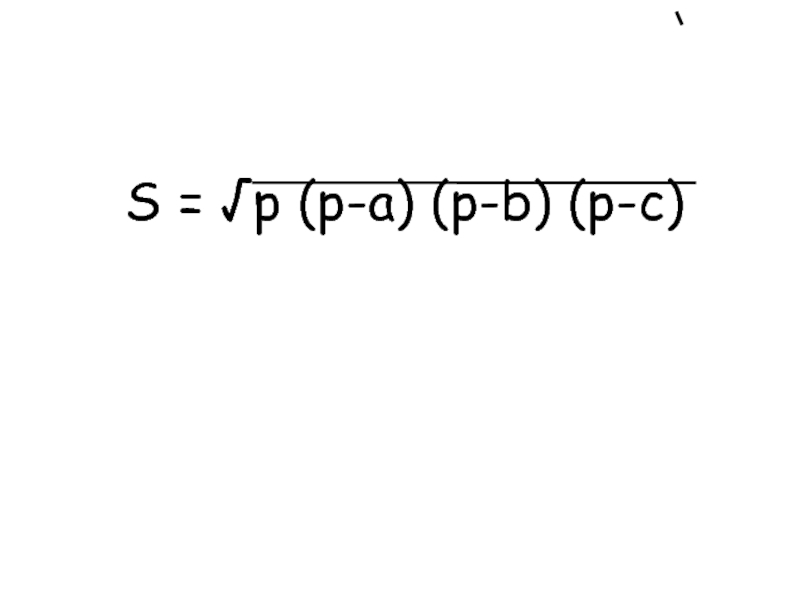Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формулы для вычисления площади треугольника 9 класс
Содержание
- 1. Формулы для вычисления площади треугольника 9 класс
- 2. Цель урока: Познакомится с формулами для вычисления
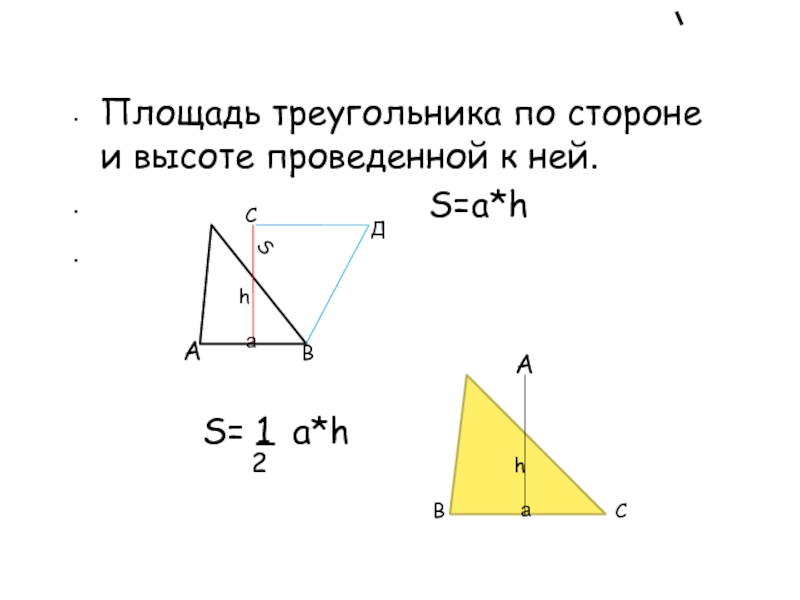
- 3. Площадь треугольника по стороне и высоте проведенной
- 4. Площадь треугольника по двум сторонам и углу
- 5. Древнегреческий математик Герон Александрийский (I в. н.э.)
- 6. Краткий вывод формулы Герона
- 7. Пусть a,b,c - стороны треугольника, а α,
- 8. p=a + b + c2
- 9. По теореме косинусов :
- 10. Слайд 10
- 11. Подставляя найденные выражения Sin α и Cos
- 12. Отсюда, применяя формулу разности квадратов, имеем:a +
- 13. S = √p (p-a) (p-b) (p-c)
- 14. Слайд 14
- 15. ∆ a2 √34 =S
- 16. Слайд 16
- 17. В СS = a*r
- 18. Слайд 18
- 19. Слайд 19
- 20. Закрепление
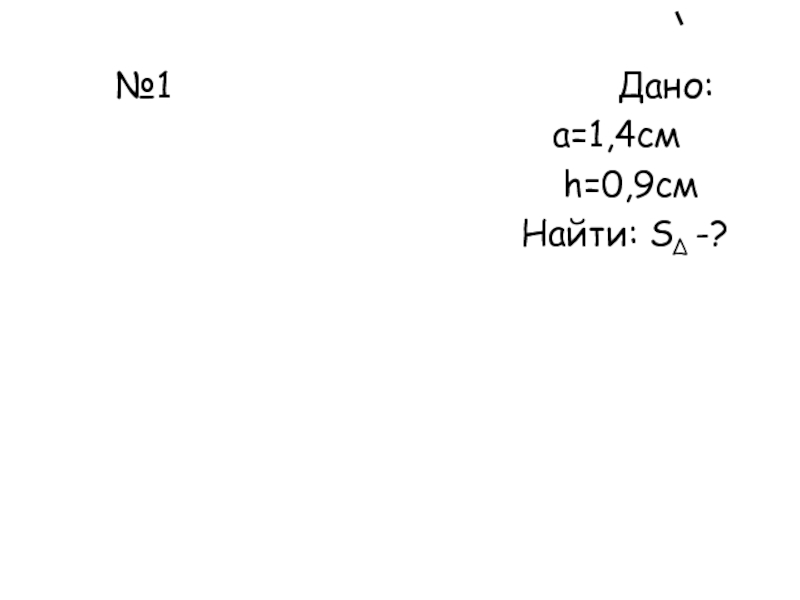
- 21. №1
- 22. №2
- 23. №3
- 24. Скачать презентанцию
Цель урока: Познакомится с формулами для вычисления площадей треугольника:а) по стороне и высоте, проведенной к этой стороне; б) по двум сторонам и углу между ними;в) формулой Геронаг ) Через радиус вписанной
Слайды и текст этой презентации
Слайд 1Презентация к уроку по геометрии в 9 классе. Тема:
«Формулы для вычисления площади треугольника»
- ПетербургСлайд 2Цель урока: Познакомится с формулами для вычисления площадей треугольника:
а) по
стороне и высоте, проведенной к этой стороне;
б) по двум
сторонам и углу между ними;в) формулой Герона
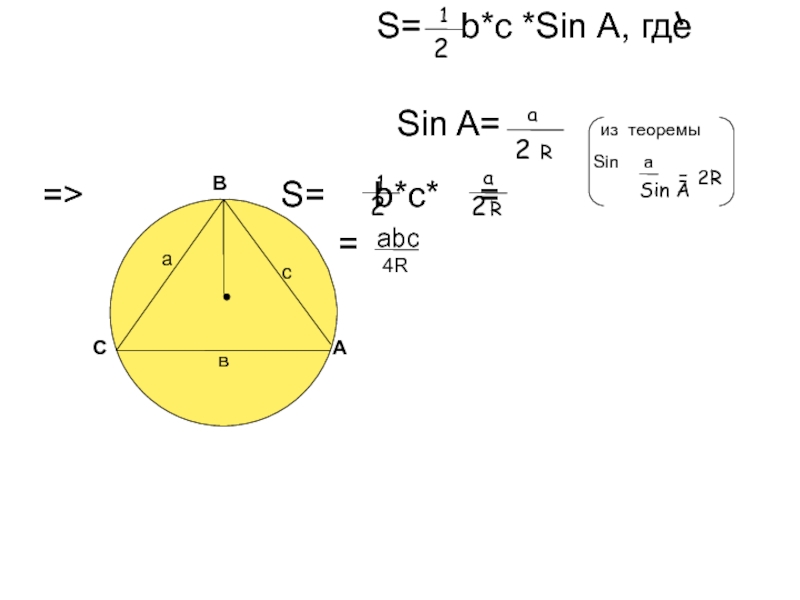
г ) Через радиус вписанной окружности и описанной окружности
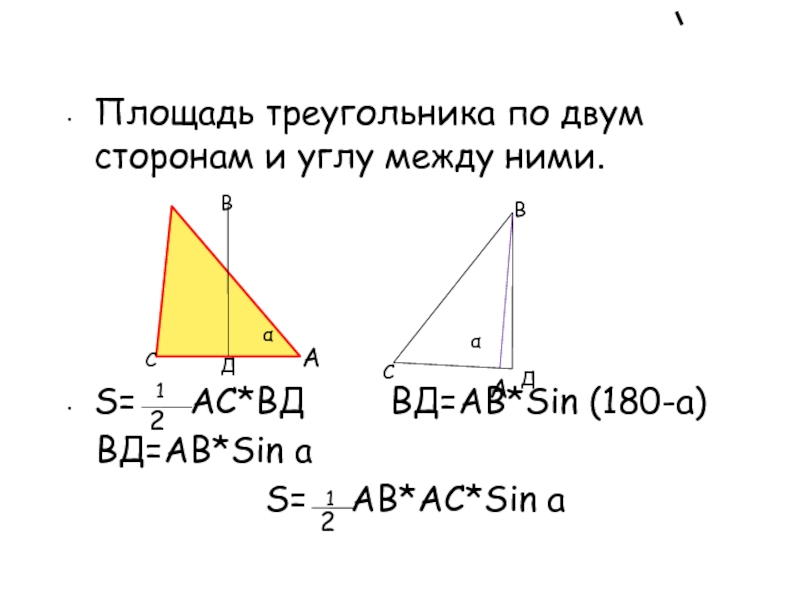
Слайд 4Площадь треугольника по двум сторонам и углу между ними.
S=
АС*ВД ВД=АВ*Sin (180-a)
ВД=АВ*Sin a
S= АВ*АС*Sin aА
А
С
С
В
В
Д
Д
α
α
1
2
1
2
Слайд 5Древнегреческий математик Герон Александрийский (I в. н.э.) Получил формулу для
вычисления площади треугольника по его трём сторонам:
S = √p (p-a) (p-b) (p-c)Слайд 7
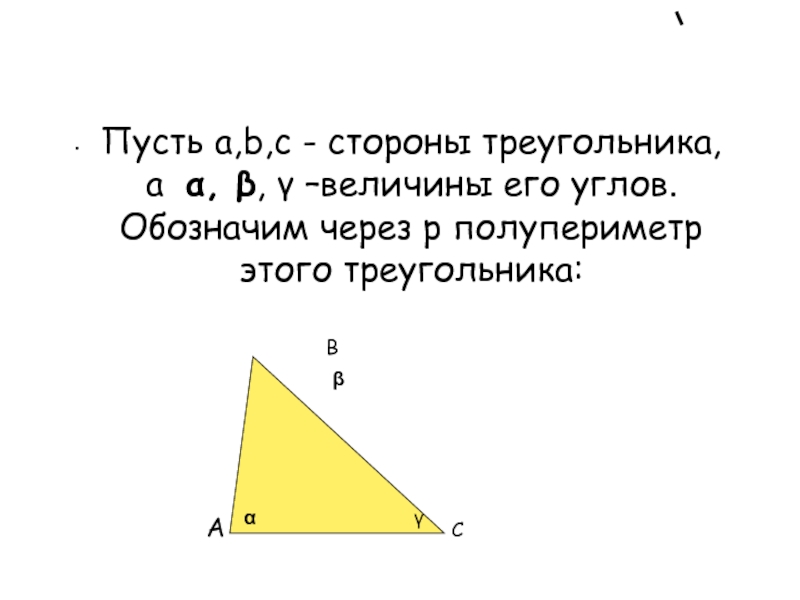
Пусть a,b,c - стороны треугольника, а α, β, γ –величины
его углов. Обозначим через p полупериметр этого треугольника:
С
В
А
α
β
γ
Слайд 11Подставляя найденные выражения
Sin α и Cos α в
формулу
Sin² α + Cos² α = 1, получим:
2S
bc
²
b²
+ c² - a²2bc
²
+
=1
Слайд 12Отсюда, применяя формулу разности квадратов, имеем:
a + b + c
2
.
b + c- a
2
.
a + b - c
2
.
a +
c- b2
=
=
p ( p – a )( p – b )( p - c)
Слайд 14 Дано:
АВС –треугольник
АВ=ВС=АС=аВывести:формулу площади треугольника
S = a*h
h= √ - =a √3
S= * a* a √3
а
а
а
h
2
a
2
1
a²
a²
4
2
1
2
2
Слайд 19
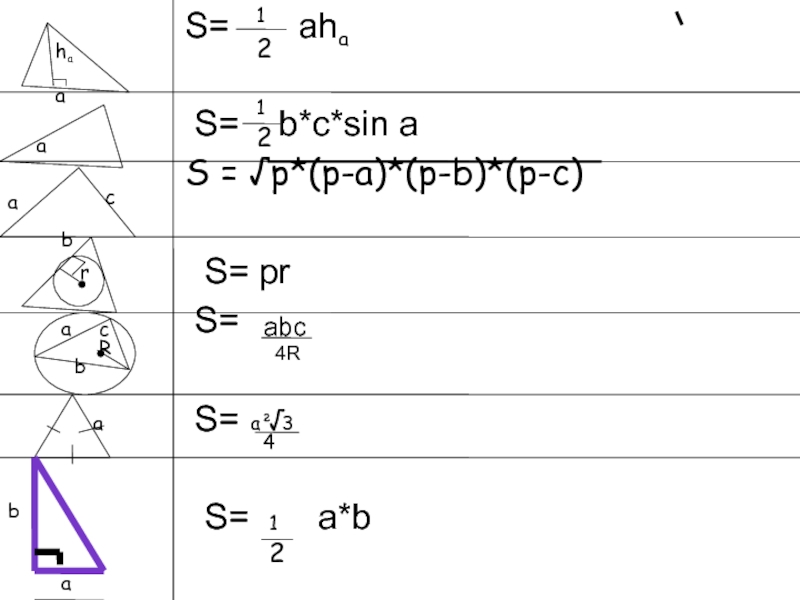
S=
ah
S= b*c*sin a S = √p*(p-a)*(p-b)*(p-c)
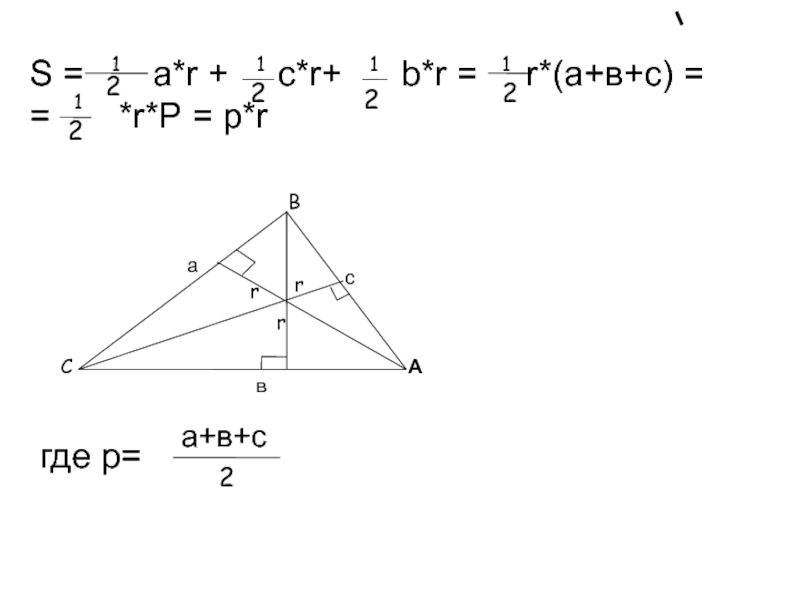
S= pr
S=
S=
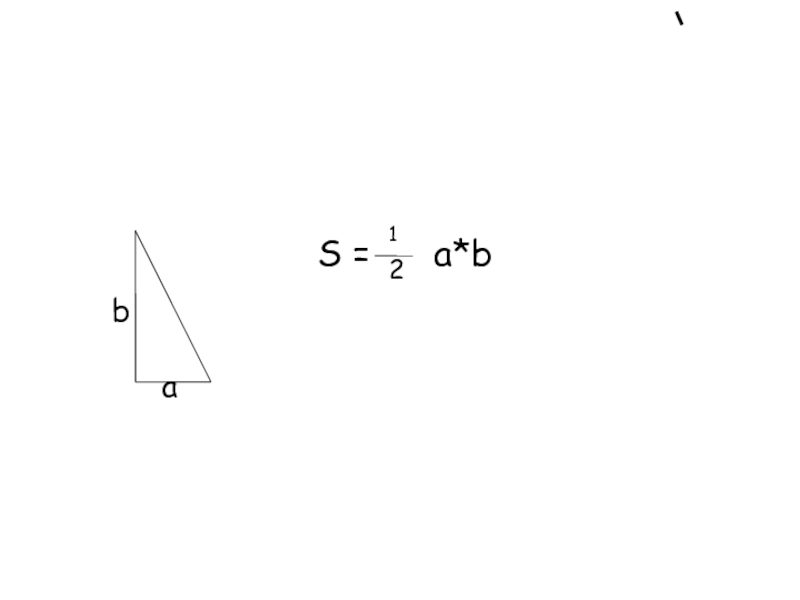
S= a*b
1
2
h
a
a
a
a
1
2
a
b
c
r
R
a
c
b
аbс
4R
a
a²
√
3
4
a
b
1
2