Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники вокруг нас 11 класс
Содержание
- 1. Многогранники вокруг нас 11 класс
- 2. В геометрии изучаются разные виды многогранников: пирамиды,
- 3. Какие многогранники являются правильными?Многогранник называется правильным, если
- 4. Как много существует правильных многогранников? (лист 1) Существует всего
- 5. Углы правильных
- 6. Теорема Эйлера: Существует ли связь между
- 7. Теорема Эйлера: В + Г – Р = 2
- 8. «Биологи» (стр. 1) Почему пчёлы строят соты именно
- 9. «Биологи» (стр. 2)Создания природы красивы и симметричны.
- 10. «Химия» Кристаллы некоторых знакомых нам веществ имеют
- 11. Кристаллы и устройство мира (стр. 1)
- 12. Кристаллы и устройство мира (стр. 2)Многие
- 13. Используемая литература1.М.Веннинджер «Модели многогранников»
- 14. Скачать презентанцию
В геометрии изучаются разные виды многогранников: пирамиды, призмы, правильные многогранники. Ни одно геометрическое тело не обладает такой красотой, как правильные многогранники. «Правильных многогранников вызывающе мало, но весьма скромный по численности
Слайды и текст этой презентации
Слайд 2 В геометрии изучаются разные виды многогранников: пирамиды, призмы, правильные многогранники.
Ни одно геометрическое тело не обладает такой красотой, как правильные
многогранники. «Правильных многогранников вызывающе мало, но весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» (Л.Кэрролл)Слайд 3Какие многогранники являются правильными?
Многогранник называется правильным, если все его грани
– равные правильные многоугольники и в каждой вершине сходится одно
и то же число гранейСлайд 4Как много существует правильных многогранников? (лист 1)
Существует всего пять таких многогранников.
Действительно,
сумма плоских углов при каждой вершине многогранного угла должна быть
меньше 360 °.Величина угла правильного многоугольника находится по формуле
n- число сторон(углов) правильного многоугольника; наименьшее количество плоских углов при вершине многогранника – 3.
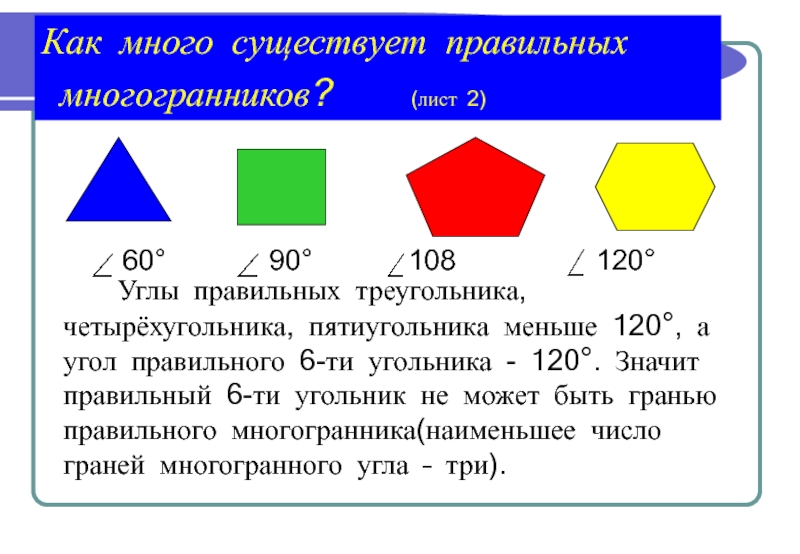
Слайд 5 Углы правильных треугольника, четырёхугольника, пятиугольника
меньше 120°, а угол правильного 6-ти угольника - 120°. Значит
правильный 6-ти угольник не может быть гранью правильного многогранника(наименьшее число граней многогранного угла – три).
60° 90° 108° 120°
Как много существует правильных
многогранников? (лист 2)
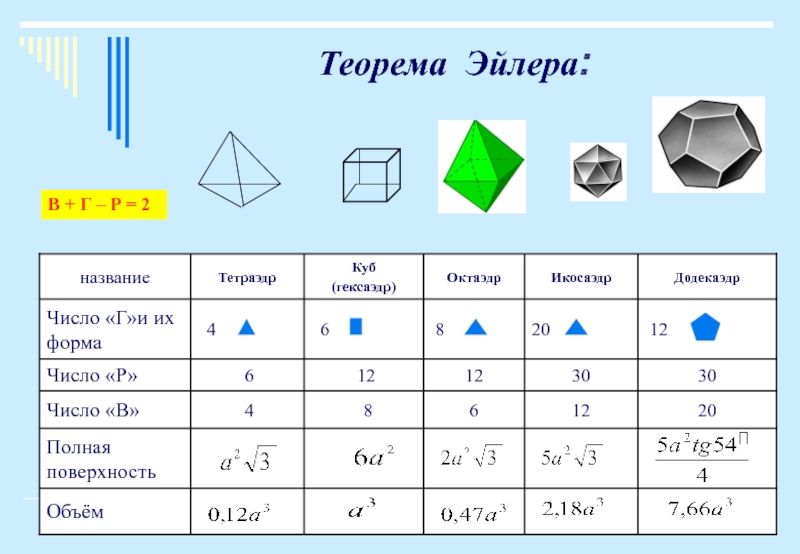
Слайд 6Теорема Эйлера:
Существует ли связь между числом вершин (В), граней
(Г), ребёр (Р) многогранника?
Ответ на этот вопрос дала теорема Эйлера:
для всякого выпуклого многогранника между числами В, Г и Р выполняется соотношение В + Г – Р = 2
число вершин - число рёбер + число граней = 2
Слайд 8«Биологи» (стр. 1)
Почему пчёлы строят соты именно так?
Пчёлы троили свои
шестиугольные соты задолго до появления человека. Пчёлы удивительные создания. Если
разрезать пчелиные соты плоскостью, то станет видна сеть равных друг другу правильных шестиугольников. Из правильных многоугольников с одинаковой площадью наименьший периметр именно у правильных шестиугольников. Стало быть, мудрые пчёлы экономят воск и время для постройки сот.Слайд 9«Биологи» (стр. 2)
Создания природы красивы и симметричны.
Феодарии –одноклеточные организмы,
форма которых точно передаёт икосаэдр. Из всех многогранников с таким
же количеством граней именно икосаэдр наибольший объём и наименьшую площадь поверхности. Это геометрическое свойств помогает морскому микроорганизму преодолевать давление водной толщи.Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Геометрические свойства икосаэдра позволяют экономить генетическую информацию.
Слайд 10«Химия»
Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников.
NaCl
–поваренная соль; форму куба имеют её кристаллы;
(KAlSO4)212H2O - монокристалл алюминиево-калиевых
квасцов имеет форму октаэдра;FeS – кристалл сернистого колчедана – форму додекаэдра;
Сурьмянистый сернокислый натрий – тетраэдр;
Бор -икосаэдр
Слайд 11Кристаллы и устройство мира
(стр. 1)
Идеи Пифагора, Платона, И.Кеплера
о связи правильных многогранников с гармоничным устройством мира и в
наше время нашли своё продолжение в интересной гипотезе, высказанной в 80-х годах 20 века московскими инженерами Марковым и Морозовым. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на все природные процессы, идущие на планете. Силовое поле кристалла обуславливает икосаэдро-додекаэдричекую структуру Земли. В земной коре как бы проступают проекции, вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Их 62 вершины и середины ребер обладают специфическими свойствами.Если нанести на глобус очаги наиболее крупных цивилизаций древности, можно заметить закономерности их расположения относительно полюсов и экватора планеты.
Слайд 12 Кристаллы и устройство мира (стр. 2)
Многие залежи полезных ископаемых
тянутся вдоль икосаэдро-додекаэдровой сетки.
Ещё более удивительные вещи происходят в местах
пересечения этих рёбер: тут располагаются очаги древних цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и др. В этих точках наблюдается максимумы и минимумы атмосферного давления, гиганские завихрения Мирового океана, здесь шотландское озеро Лох-несс, Бермудский треугольник.Возможно в будущем, исследования Земли определят отношение к этой красивой научной гипотезе, в которой правильные многогранники играют такое важное место.
Слайд 13 Используемая литература
1.М.Веннинджер «Модели многогранников»
пер.с англ. В.В.Фирсова
под ред. И.М.Яглома., М., «Мир», 1974
2. Пойа Д., «Математика и
правдоподобные рассуждения», М., ИЛ, 19573. М.Я.Выгодский «Справочник по элементарной математике» , «Наука», М., 1976
4. «Я познаю мир, детская энциклопедия, Математика,» Москва, Астрель, 2002
5. «Энциклопедия юного математика», Москва , 1980 г
6. «Математика» учебно-методическая газета 2005 г