Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Число π (пи)
Содержание
- 1. Число π (пи)
- 2. Автор: Карелина ИринаРуководитель: Никифорова М. Н.,
- 3. Цели:Познакомить с числом π.Провести практическую работу нахождения
- 4. Число π (пи)Число π — математическая константа,
- 5. 3. 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944
- 6. ИсторияВпервые обозначением этого числа греческой буквой воспользовался
- 7. Иррациональность числаπ — иррациональное число, то есть
- 8. Трансцендентность числаπ — трансцендентное число, это означает,
- 9. Формулы с числомФрансуа Виет, 1593: Формула Валлиса:Ряд Лейбница:
- 10. Длина окружностиТеорема 9.6. Отношение длины окружности к ее
- 11. Проведём практическую работу.Возьмём 5 любых предметов: теннисный мяч, стакан, кружку, баночку, банку для теннисных мячей.
- 12. Завяжем предметы ниткой и таким образом мы измерим длину окружности.
- 13. Измерим диаметр предмета
- 14. Составим таблицу по найденным нами даннымВывод: отношение длины окружности к диаметру приближается к 3,14
- 15. Международный день числа «Пи» 14
- 16. "Пи" с детства знакомо любому из нас
- 17. В Сиэтле есть даже памятник числу "пи".
- 18. Рекорд запоминания числа π Запомнить знаки p
- 19. Про число p — 3,1415926...
- 20. Мнемонические правилаЧтобы нам не ошибаться, Надо правильно
- 21. www.calend.ru/holidays/0/0/1919/ http://crow.academy.ru/dm/materials_/pi/mem.htmhttp://ru.wikipedia.org/wiki/Pi
- 22. Скачать презентанцию
Автор: Карелина ИринаРуководитель: Никифорова М. Н., учитель математики ЮВАО ГОУ СОШ № 1968 Москва 2009-2010г.
Слайды и текст этой презентации
Слайд 3Цели:
Познакомить с числом π.
Провести практическую работу нахождения числа π.
Выяснить практическое
значение числа π.
Найти мнемонические правила для запоминания.
Слайд 4Число π (пи)
Число π — математическая константа, выражающая отношение длины
окружности к длине ее диаметра. В цифровом выражении π начинается
как 3,141592 и имеет бесконечную математическую продолжительность.Слайд 5
3.
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 0604009277 0167113900 9848824012 8583616035 6370766010 4710181942 9555961989 4676783744 9448255379 7747268471 0404753464 6208046684 2590694912 9331367702 8989152104 7521620569 6602405803 8150193511 2533824300 3558764024 7496473263На сегодняшней день значение числа ПИ известно, оно равно:
Слайд 6История
Впервые обозначением этого числа греческой буквой воспользовался британский математик Джонс(1706),
а общепринятым оно стало после работ Леонарда Эйлера в 1737.
Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.Слайд 7Иррациональность числа
π — иррациональное число, то есть его значение не
может быть точно выражено в виде дроби m/n, где m
и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа π была впервые доказана Иоганном Ламбертом в 1767 году путём разложения числа в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π и π2.Слайд 8Трансцендентность числа
π — трансцендентное число, это означает, что оно не
может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа
π была доказана в 1882 году профессором Кенигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.Поскольку в геометрии Евклида площадь круга и длина окружности являются функциями числа π, то доказательство трансцендентности π положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.
Слайд 10Длина окружности
Теорема 9.6. Отношение длины окружности к ее радиусу не зависит
от окружности.
Доказательство
Возьмем две произвольные окружности ω1и ω2. Пусть R1
и R2 – их радиусы, а l1 и l2 – их длины соответственно. Допустим, что утверждение теоремы неверно и Пусть
Впишем в окружности правильные многоугольники. При достаточно больших n длины окружностей ω1 и ω2 будут сколь угодно мало отличаться от периметров вписанных многоугольников P1 и P2 соответственно. Это значит, можно так подобрать n, что l1 – P1 = δ1 > 0 и l2 – P2 = δ2 > 0. Подставим выражения для l1 и l2 из этих равенств в предполагаемое неравенство: Но по следствию 9.3 и отсюда Здесь ε – фиксированное число, δ1 и δ2 могут быть сделаны очень маленькими за счет выбора очень большого n. Например, за счет выбора n можно сделать Тогда, очевидно, что приводит к противоречию. Теорема доказана.
Отношение длины окружности к диаметру принято обозначать греческой буквой π (читается «пи»). Отсюда длина окружности вычисляется по формуле
Слайд 11Проведём практическую работу.
Возьмём 5 любых предметов: теннисный мяч, стакан, кружку,
баночку, банку для теннисных мячей.
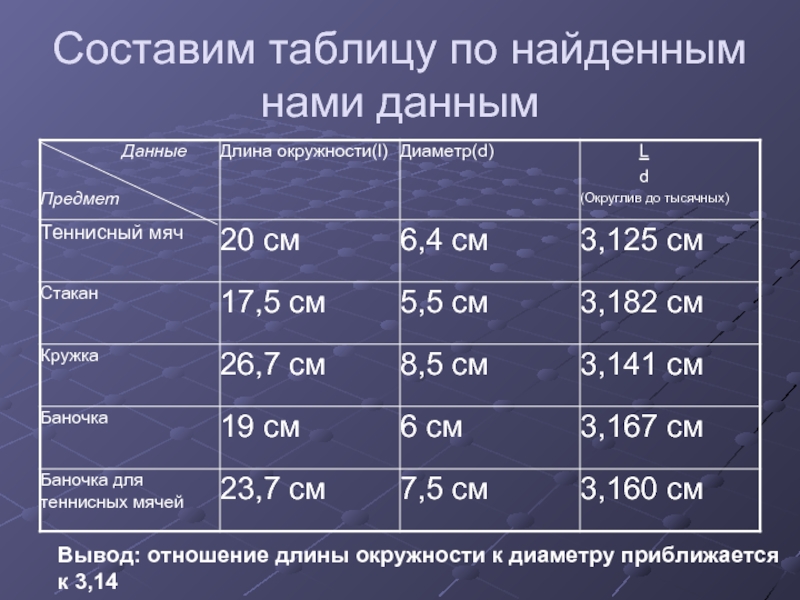
Слайд 14Составим таблицу по найденным нами данным
Вывод: отношение длины окружности к
диаметру приближается к 3,14
Слайд 15
Международный день числа «Пи»
14 марта в мире отмечается один из
самых необычных праздников – «День числа Пи».
В американском написании
сегодняшняя дата выглядит как 3.14, отсюда и объяснение, почему именно в этот день отмечается этот праздник.
Как считают специалисты, это число было открыто вавилонскими магами. Оно использовалось при строительстве знаменитой Вавилонской башни. Однако недостаточно точное исчисление значения Пи привело к краху всего проекта. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона.
Знаменательно, что праздник числа Пи совпадает с днем рождения одного из наиболее выдающихся физиков современности - Альберта Эйнштейна. Слайд 16"Пи" с детства знакомо любому из нас по множеству математических
и физических формул. Одна такая формула попала в роспись коридора
главного корпуса КПИ возле Большой физической аудитории (художники Л. и Т.Дмитренко):Вот она, справа от Нильса Бора, слева от Альберта Эйнштейна. Насколько могу судить, это квантовое условие Бора с обозначением радиуса орбиты электрона через "а".
Слайд 18Рекорд запоминания числа π
Запомнить знаки p человечество пытается уже
давно. Но как уложить в память бесконечность? Любимый вопрос мнемонистов-профессионалов.
Разработано множество уникальных теорий и приёмов освоения огромного количества информации. Многие из них опробованы на p.Мировой рекорд, установленный в прошлом столетии в Германии - 40 000 знаков. Российский рекорд значений числа p 1 декабря 2003 года в Челябинске установил Александр Беляев. За полтора часа с небольшими перерывами на школьной доске Александр написал 2500 цифр числа p.
До этого рекордным в России считалось перечислить 2000 знаков, что удалось сделать в 1999 году в Екатеринбурге. По словам Александра Беляева - руководителя центра развития образной памяти, такой эксперимент со своей памятью может провести любой из нас. Важно лишь знать специальные техники запоминания и периодически тренироваться.
Слайд 19Про число p — 3,1415926...
Гордый Рим трубил
победу Над твердыней Сиракуз; Но трудами Архимеда Много больше я горжусь. Надо нынче нам
заняться, Оказать старинке честь, Чтобы нам не ошибаться, Чтоб окружность верно счесть, Надо только постараться И запомнить все как есть Три — четырнадцать — пятнадцать — девяносто два ишесть!
С.Бобров
Слайд 20Мнемонические правила
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два
и шесть. Надо только постараться И запомнить всё как есть: Три, четырнадцать, пятнадцать, Девяносто
два и шесть. Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься, Это каждый должен знать. Можно просто постараться И почаще повторять: «Три, четырнадцать, пятнадцать, Девять, двадцать шесть и пять».Слайд 21
www.calend.ru/holidays/0/0/1919/
http://crow.academy.ru/dm/materials_/pi/mem.htm
http://ru.wikipedia.org/wiki/Pi
Теги