Разделы презентаций

ЕГЭ 2016, вариант - 1

Содержание

1.Ма­га­зин за­ку­па­ет цве­точ­ные горш­ки по опто­вой цене 100 руб­лей за штуку и про­да­ет с на­цен­кой 30%. Какое наи­боль­шее число таких горш­ков можно ку­пить в этом ма­га­зи­не на 1200 руб­лей? Ре­ше­ние.С уче­том на­цен­ки гор­шок

Слайды и текст этой презентации

Слайд 1ЕГЭ 2016г. Вар-1
Автор Магометова Х. Н.МБОУ «СОШ №1
с.Кизляр».

2016

ЕГЭ 2016г. Вар-1 Автор Магометова Х. Н.МБОУ «СОШ №1 с.Кизляр».2016

Слайд 21.Ма­га­зин за­ку­па­ет цве­точ­ные горш­ки по опто­вой цене 100 руб­лей за штуку

и про­да­ет с на­цен­кой 30%. Какое наи­боль­шее число таких горш­ков

можно ку­пить в этом ма­га­зи­не на 1200 руб­лей?


Ре­ше­ние.
С уче­том на­цен­ки гор­шок ста­нет сто­ить 100 + 0,3 


 100 = 130 руб­лей. Раз­де­лим 1200 на 130:
 

.

Зна­чит, можно будет ку­пить 9 горш­ков.
 
Ответ: 9.

1.Ма­га­зин за­ку­па­ет цве­точ­ные горш­ки по опто­вой цене 100 руб­лей за штуку и про­да­ет с на­цен­кой 30%. Какое наи­боль­шее

Слайд 32 . На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в

Сочи за каж­дый месяц 1920 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы,

по вер­ти­ка­ли - тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Для на­гляд­но­сти жир­ные точки со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­мень­шую сред­не­ме­сяч­ную тем­пе­ра­ту­ру в пе­ри­од с мая по де­кабрь 1920 года. Ответ дайте в гра­ду­сах Цель­сия.
 

 

Ре­ше­ние.
Из гра­фи­ка видно, что наи­мень­шая сред­не­ме­сяч­ная тем­пе­ра­ту­ра в пе­ри­од с пя­то­го по две­на­дца­тый месяц (с мая по де­кабрь) была в но­яб­ре и со­став­ля­ла 6 °C (см. ри­су­нок).
 
Ответ: 6.

2 . На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Сочи за каж­дый месяц 1920 года. По

Слайд 43.  
Век­тор
с концами в точке В(5; 3)

имеет ко­ор­ди­на­ты (3; 1). Най­ди­те ординату точки А
.
Ре­ше­ние.
Ко­ор­ди­на­ты век­то­ра равны

раз­но­сти ко­ор­ди­нат конца век­то­ра и его на­ча­ла. Ко­ор­ди­на­ты точки A вы­чис­ля­ют­ся сле­ду­ю­щим об­ра­зом: 5 − x = 3, 3 − y = 1. От­ку­да x = 2, y = 2.
 
Ответ: 2.
3.   Век­тор с концами в точке В(5; 3) имеет ко­ор­ди­на­ты (3; 1). Най­ди­те ординату точки А.Ре­ше­ние.Ко­ор­ди­на­ты

Слайд 54. Фаб­ри­ка вы­пус­ка­ет сумки. В сред­нем на 200 ка­че­ствен­ных сумок

при­хо­дит­ся че­ты­ре сумки со скры­ты­ми де­фек­та­ми. Най­ди­те ве­ро­ят­ность того, что

куп­лен­ная сумка ока­жет­ся ка­че­ствен­ной. Ре­зуль­тат округ­ли­те до сотых.
Ре­ше­ние.
По усло­вию из любых 200 + 4 = 204 сумок в сред­нем 200 ка­че­ствен­ных сумок. Зна­чит, ве­ро­ят­ность того, что куп­лен­ная сумка ока­жет­ся ка­че­ствен­ной, равна
 

 
Ответ: 0,98.

4. Фаб­ри­ка вы­пус­ка­ет сумки. В сред­нем на 200 ка­че­ствен­ных сумок при­хо­дит­ся че­ты­ре сумки со скры­ты­ми де­фек­та­ми. Най­ди­те

Слайд 65. Най­ди­те ко­рень урав­не­ния
.
Ре­ше­ние.
По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: −4.

5. Най­ди­те ко­рень урав­не­ния .Ре­ше­ние.По­сле­до­ва­тель­но по­лу­ча­ем:Ответ: −4.

Слайд 76.
В тре­уголь­ни­ке АВС, угол С
равен 90°,
– вы­со­та, угол

А= 34
. Най­ди­те угол ВСН
. Ответ

дайте в гра­ду­сах.

Ре­ше­ние.
углы А и ВСН

равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми, зна­чит,
 

.
Ответ: 34.

6. В тре­уголь­ни­ке АВС, угол Сравен 90°, – вы­со­та, угол А= 34 . Най­ди­те угол ВСН

Слайд 87.
Пря­мая
яв­ля­ет­ся ка­са­тель­ной к гра­фи­ку функ­ции






Ре­ше­ние.
Усло­вие ка­са­ния гра­фи­ка

функ­ции
и пря­мой
задаётся си­сте­мой тре­бо­ва­ний:
 

 
В нашем слу­чае имеем:
 

 
Ответ: 17.


Най­ди­те c.

7. Пря­мая яв­ля­ет­ся ка­са­тель­ной к гра­фи­ку функ­ции Ре­ше­ние.Усло­вие ка­са­ния гра­фи­ка функ­ции и пря­мой задаётся си­сте­мой тре­бо­ва­ний:  В нашем

Слайд 98.
Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки
па­рал­ле­ле­пи­пе­да
,

у ко­то­ро­го
.
Па­рал­ле­ле­пи­пед пря­мо­уголь­ный.
Ре­ше­ние.

Из ри­сун­ка видно, что мно­го­гран­ник яв­ля­ет­ся

по­ло­ви­ной дан­но­го па­рал­ле­ле­пи­пе­да. Сле­до­ва­тель­но, его объём равен по­ло­ви­не объёма ис­ход­но­го пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да:

 

 
 
Ответ: 120.

8. Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки па­рал­ле­ле­пи­пе­да , у ко­то­ро­го .Па­рал­ле­ле­пи­пед пря­мо­уголь­ный. Ре­ше­ние.Из ри­сун­ка видно,

Слайд 109.
Най­ди­те зна­че­ние вы­ра­же­ния
.
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:

.
Ответ: −6.

9. Най­ди­те зна­че­ние вы­ра­же­ния .Ре­ше­ние.Вы­пол­ним пре­об­ра­зо­ва­ния: .Ответ: −6.

Слайд 1110. Де­та­лью не­ко­то­ро­го при­бо­ра яв­ля­ет­ся квад­рат­ная рамка с на­мо­тан­ным на

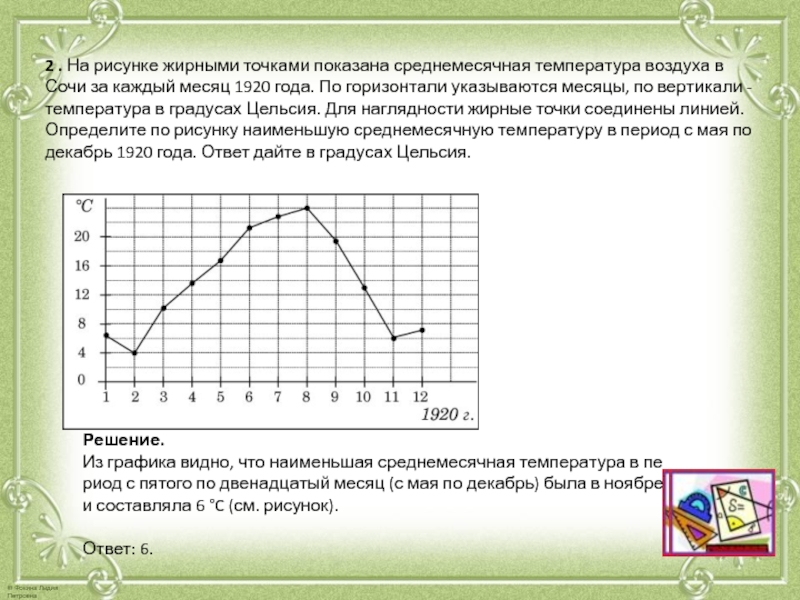
неe про­во­дом, через ко­то­рый про­пу­щен по­сто­ян­ный ток. Рамка по­ме­ще­на в

од­но­род­ное маг­нит­ное поле так, что она может вра­щать­ся. Мо­мент силы Ам­пе­ра, стре­мя­щей­ся по­вер­нуть рамку, (в Н

м) опре­де­ля­ет­ся фор­му­лой

, где

– сила тока в рамке,

Тл – зна­че­ние ин­дук­ции маг­нит­но­го поля,

раз­мер рамки,

– число вит­ков про­во­да в рамке,

– ост­рый угол между пер­пен­ди­ку­ля­ром к рамке и век­то­ром ин­дук­ции. При каком наи­мень­шем зна­че­нии угла

(в гра­ду­сах) рамка может на­чать вра­щать­ся, если для этого нужно, чтобы рас­кру­чи­ва­ю­щий мо­мент M был не мень­ше 0,75 Нм?


Ре­ше­ние.
За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства

на ин­тер­ва­ле

при за­дан­ных зна­че­ни­ях силы тока в рамке

, раз­ме­ра рамки

м, числа вит­ков про­во­да

и ин­дук­ции маг­нит­но­го поля

Тл:
 

.
Ответ: 30.

10. Де­та­лью не­ко­то­ро­го при­бо­ра яв­ля­ет­ся квад­рат­ная рамка с на­мо­тан­ным на неe про­во­дом, через ко­то­рый про­пу­щен по­сто­ян­ный ток.

Слайд 1211. Из одной точки кру­го­вой трас­сы, длина ко­то­рой равна 12

км, од­но­вре­мен­но в одном на­прав­ле­нии стар­то­ва­ли два ав­то­мо­би­ля. Ско­рость пер­во­го

ав­то­мо­би­ля равна 106 км/ч, и через 48 минут после стар­та он опе­ре­жал вто­рой ав­то­мо­биль на один круг. Най­ди­те ско­рость вто­ро­го ав­то­мо­би­ля. Ответ дайте в км/ч.
Ре­ше­ние.
Пусть ско­рость вто­ро­го ав­то­мо­би­ля равна км/ч.

За 4/5 часа пер­вый ав­то­мо­биль про­шел на 12 км боль­ше, чем вто­рой, от­сю­да имеем

Ответ: 91.

11. Из одной точки кру­го­вой трас­сы, длина ко­то­рой равна 12 км, од­но­вре­мен­но в одном на­прав­ле­нии стар­то­ва­ли два

Слайд 1312. Най­ди­те наи­боль­шее зна­че­ние функ­ции
на от­рез­ке
.
Ре­ше­ние.
Най­дем про­из­вод­ную за­дан­ной

функ­ции:
 

Най­дем нули про­из­вод­ной на за­дан­ном от­рез­ке:
 

 
Опре­де­лим знаки про­из­вод­ной

функ­ции на за­дан­ном от­рез­ке и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

В точке

за­дан­ная функ­ция имеет мак­си­мум, яв­ля­ю­щий­ся ее наи­боль­шим зна­че­ни­ем на за­дан­ном от­рез­ке. Най­дем это наи­боль­шее зна­че­ние:
 

.
Ответ: −3.

12. Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .Ре­ше­ние.Най­дем про­из­вод­ную за­дан­ной функ­ции:  Най­дем нули про­из­вод­ной на за­дан­ном от­рез­ке:

Слайд 17Информационные источники
http://urokidoma.org/?utm_source=reshuege&utm_medium=banner&utm_campaign=urokidoma&utm_content=top&utm_term=ud_banner5_728x90
http://решуегэ.рф/
http://решуегэ.рф/
http://решуегэ.рф/
© Гущин Д. Д., 2011—2015

Информационные источникиhttp://urokidoma.org/?utm_source=reshuege&utm_medium=banner&utm_campaign=urokidoma&utm_content=top&utm_term=ud_banner5_728x90http://решуегэ.рф/http://решуегэ.рф/http://решуегэ.рф/© Гущин Д. Д., 2011—2015

Похожие презентации

Первый признак равенства треугольников Первый признак равенства треугольников 373
Элементы статистики Элементы статистики 650
В начале было число... В начале было число... 242
Построение графика функции 10 класс Построение графика функции 10 класс 311
Формирование функциональной грамотности на уроках математики Формирование функциональной грамотности на уроках математики 475
Расчет пути и времени движения Расчет пути и времени движения 328
Старинные меры длины и веса Старинные меры длины и веса 361
Обыкновенные дроби 5 класс Обыкновенные дроби 5 класс 381
Сравнение углов Сравнение углов 417
Использование пакета программ Microsoft Office в повседневной работе педагога Использование пакета программ Microsoft Office в повседневной работе педагога 369
Десятичные дроби. Действия с десятичными дробями Десятичные дроби. Действия с десятичными дробями 291
Урок-путешествие. Километр 4 класс Урок-путешествие. Километр 4 класс 387
"?ыс?аша к?бейту" та?ырыбыны? жоспары 372
Задачи на увеличение и уменьшение числа (1 класс) Задачи на увеличение и уменьшение числа (1 класс) 471
Ломаная Ломаная 412
Виды вкладов и расчет накоплений Виды вкладов и расчет накоплений 335
Использование ИКТ на уроках математики Использование ИКТ на уроках математики 318
Ауданды олшеу Ауданды олшеу 506
Екі өрнектің кубтарының қосындысы Екі өрнектің кубтарының қосындысы 339
Числа-великаны Числа-великаны 785

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика