Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы статистики
Содержание
- 1. Элементы статистики
- 2. Слово « статистика» происходит от латинского status
- 3. 2. Статистика – это отрасль практической деятельности,
- 4. Случайная величина.Одно из самых важных понятий в
- 5. Статистическая информация о результатах наблюдений или экспериментов
- 6. Отдельные значения Хi ,
- 7. Игральный кубик бросили 12 раз и записали
- 8. Представим ряд данных 3,4,5,6,6,6,5,1,4,6,1,4 в виде таблицы
- 9. Относительная частота.Относительной частотой события А в данной
- 10. Рост каждой из 50 гимнасток одного клуба
- 11. Слайд 11
- 12. Полигоны частот Распределение случайных величин можно
- 13. В координатной плоскости на оси абсцисс будем
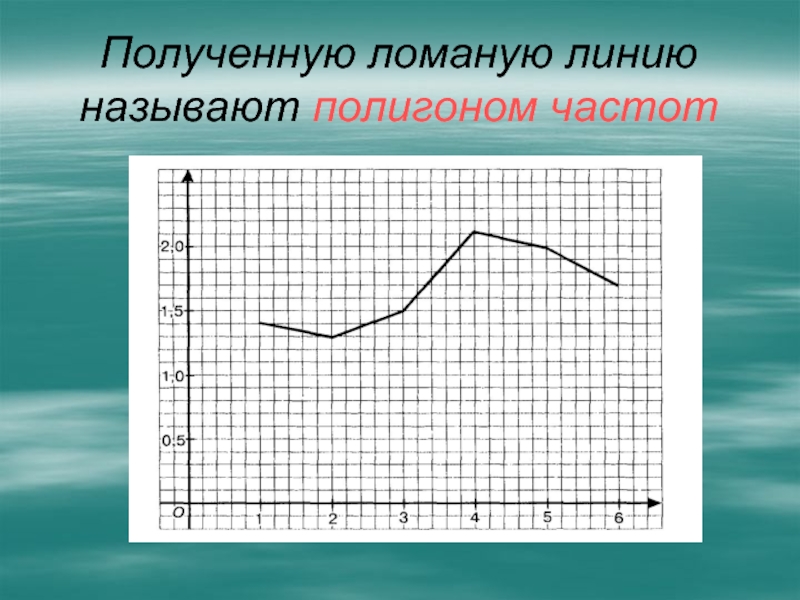
- 14. Полученную ломаную линию называют полигоном частот
- 15. Размах, мода, Медиана.Размах (R) – разность между
- 16. Даны таблицы: 1) распределения
- 17. Слайд 17
- 18. Заданные таблицами распределения величин Х и У
- 19. Рассмотрим ряд (1) 3,3,3,4,4,5,5,5,8,12.В ряду (1) 10
- 20. Рассмотрим ряд (2) 3, 3,
- 21. Найти размах, моду и медиану
- 22. Среднее значение Средним значением случайнойвеличины Х ( Х ) называют среднее арифметическое всех ее значений.
- 23. ЗадачаНа соревнованиях по фигурному катанию судьи поставили
- 24. Решение:Среднее арифметическое Х~5,32 характеризует средний уровень оценок.Размах
- 25. Выборочная дисперсия D(Х) есть среднее значение квадратовотклонений всех вариант от среднегозначения ряда.
- 26. Сравнить дисперсии выборок 4,6,8,9,8 и 6,8,10,12,9
- 27. ЗадачаДвух футболистов, один из которых участвовал в
- 28. Решение:Находим числовые характеристики двух выборок:Первый футболист:Второй футболист:Таким
- 29. Самостоятельная работа «Наибольшее и наименьшее значение. Размах».1.Укажите
- 30. Самостоятельная работа «Среднее арифметическое».1.На координатной прямой
- 31. Самостоятельная работа «Медиана. Мода».1. Найдите медианы
- 32. Скачать презентанцию
Слово « статистика» происходит от латинского status ( состояние, положение вещей).1. Статистика – это научное направление (комплекс наук), объединяющее принципы и методы работы с числовыми данными, характеризующими массовые явления.
Слайды и текст этой презентации
Слайд 1Элементы статистики.
Автор: Крячко Н.В.
учитель математики МБОУ «Лицей №3
г.Саров Нижегородской области
Слайд 2Слово « статистика» происходит от латинского status ( состояние, положение
вещей).
и методы работы с числовыми данными, характеризующими массовые явления.Слайд 32. Статистика – это отрасль практической деятельности, направленной на сбор,
обработку, анализ статистических данных.
3. Статистика –это совокупность статистических данных, характеризующих
какое –нибудь явление или процесс (например, статистика рождаемости и смертности в России, статистика успеваемости учащихся и т.п.).Слайд 4Случайная величина.
Одно из самых важных понятий в теории вероятностей –
случайная величина.
Случайной величиной называется переменная величина, значения которой зависят от
случайного исхода некоторого испытания.Слайд 5Статистическая информация о результатах наблюдений или экспериментов может быть представлена
в различных формах.
Простейшей из них является запись в порядке их
появления – запись в ряд:называемый простым статистическим рядом или выборкой.
Слайд 6Отдельные значения Хi , составляющие этот ряд,
называют вариантами или просто данными.
Количество вариант в ряду n называют
объемом ряда, или объемом выборки.Варианты в ряду могут иметь как различные, так и одинаковые значения.
Слайд 7Игральный кубик бросили 12 раз и записали выпавшие числа в
порядке их появления
3,4,5,6,6,6,5,1,4,6,1,4 ( n = 12 ).
Вариантами в ряду
являются Варианты имеют одинаковые значения.
Слайд 8Представим ряд данных 3,4,5,6,6,6,5,1,4,6,1,4 в виде таблицы
В первой строке
– значение случайной величины Х, во второй – частота значений
варианты М.Слайд 9Относительная частота.
Относительной частотой события А в данной серии испытаний называют
отношение частоты М события А к числу всех проведенных испытаний
N.W(A) =
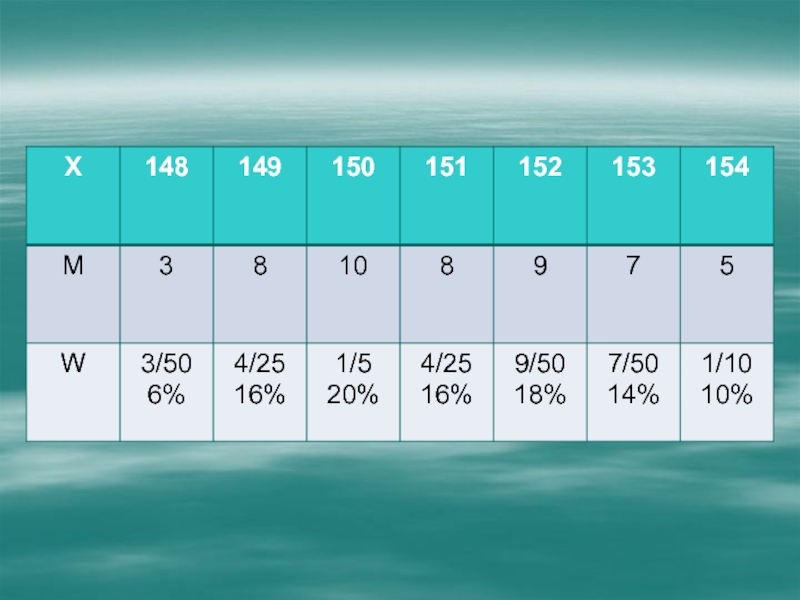
Слайд 10Рост каждой из 50 гимнасток одного клуба занесен в таблицу
По
имеющимся данным составить таблицу распределения значений роста гимнасток
1)
по частотам М; 2) по относительным частотам W.Слайд 12Полигоны частот
Распределение случайных величин можно задавать и демонстрировать
графически.
Рассмотрим пример.
В первом полугодии 2011 года завод получил
прибыль в 10 млн. рублей. Распределение прибыли по месяцам показано в таблицеСлайд 13В координатной плоскости на оси абсцисс будем отмечать номер месяца
(янв. – 1, февр. – 2 и т.д.). На оси
ординат будем отмечать прибыль завода (в млн. руб.).Отметим точки (1;1,4),(2;1,3),(3;1,5),(4;2,1),(5;2),(6;1,7) и соединим их последовательно отрезками
Слайд 15Размах, мода, Медиана.
Размах (R) – разность между наибольшим и наименьшим
значениями варианты.
Мода (Мо) – наиболее часто встречающееся значение варианты в
ряду.Медиана ( Ме) – это серединное значение упорядоченного ряда значений случайной величины.
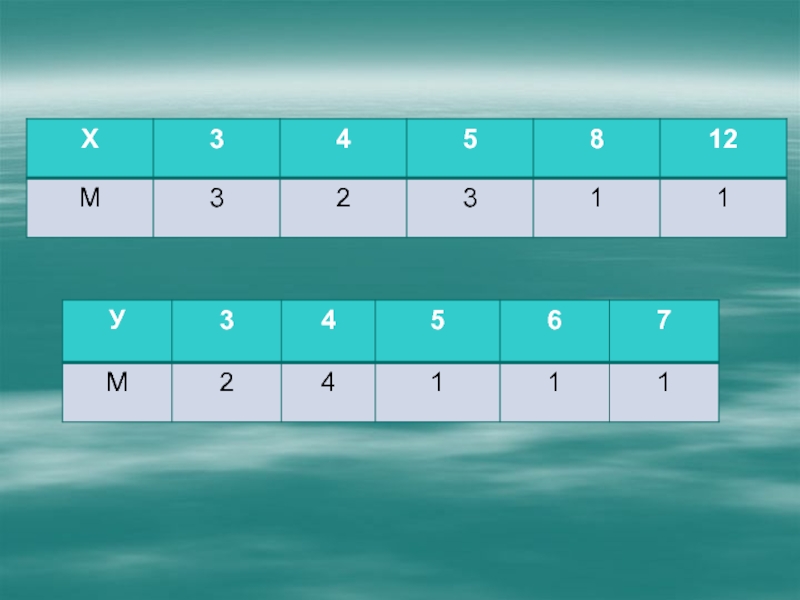
Слайд 16 Даны таблицы:
1) распределения случайной величины Х
– числа прочитанных за каникулы книг 10 девочками по
частотам М,2)распределения по частотам случайной величины У – числа прочитанных книг 9 мальчиками.
Слайд 18Заданные таблицами распределения величин Х и У могут быть записаны
в виде следующих рядов:
3, 3,
3, 4, 4, 5, 5, 5, 8, 12; (1)3, 3, 4, 4, 4, 4, 5, 6, 7 . (2)
Для совокупности (1) R = 12 – 3 =9,
Для совокупности (2) R = 7-3=4.
В ряду (1) две моды: Мо1=3, Мо2=5.
В ряду (2) : Мо = 4.
Слайд 19Рассмотрим ряд (1) 3,3,3,4,4,5,5,5,8,12.
В ряду (1) 10 членов – четное
число. Для него медиана равна среднему арифметическому
двух центральных значений пятого и шестого:Ме = (4+5):2=4,5.
Слайд 20 Рассмотрим ряд (2) 3, 3, 4, 4, 4,
4, 5, 6, 7.
В ряду (2) – нечетное число элементов.
Его медиана равна значению центрального пятого члена ряда:Ме=4.
Слайд 21Найти размах, моду и медиану
совокупности: -2, 3,
4, -3, 0, 1, 3, -2, -1, 2,
-2, 1.Решение:
Запишем данные в виде упорядоченного ряда: -3, -2, -2, -2, -1, 0, 1, 1, 2, 3, 3, 4.
R = 4 – (-3) = 7.
Мо = - 2.
Ме= (0+1):2=0,5.
Слайд 22Среднее значение
Средним значением случайной
величины Х ( Х ) называют
среднее арифметическое всех ее значений.
Слайд 23Задача
На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки:
5,2 5,4 5,5 5,4 5,1
5,1 5,4 5,5 5,3Для полученного ряда чисел найдите среднее арифметическое, размах, медиану и моду.
Что характеризует каждый из этих показателей?
Слайд 24Решение:
Среднее арифметическое Х~5,32 характеризует средний уровень оценок.
Размах А = хmax-хmin=5,5-5,1=0,4
характеризует разброс оценок.
Мода Мо=5,4 показывает оценку, которая встречается чаще других.
Медиана
Ме=5,4 показывает, что половина членов ряда не превосходит по величине 5,4.Слайд 25Выборочная дисперсия D(Х)
есть среднее значение квадратов
отклонений всех вариант от
среднего
значения ряда.
Слайд 26Сравнить дисперсии выборок 4,6,8,9,8 и 6,8,10,12,9
1) n=5;
2) n=5;
Дисперсия второй выборки больше.
Слайд 27Задача
Двух футболистов, один из которых участвовал в пяти игровых сезонах,
а другой – в шести, сравнить по результативности и стабильности
в забивании голов, если количество мячей, забитых первым футболистом по сезонам образует ряд: 17,21,20,16,15,19,а вторым: 17,20,18,21,14.
Слайд 28Решение:
Находим числовые характеристики двух выборок:
Первый футболист:
Второй футболист:
Таким образом, оба футболиста
показывают одинаковую результативность(среднее число голов за сезон), но первый футболист
более стабилен, так как дисперсия первой выборки меньше.Слайд 29Самостоятельная работа «Наибольшее и наименьшее значение. Размах».
1.Укажите наибольшее и наименьшее
значение и размах набора чисел : 0;-2;19.
2.Даны два набора чисел:
5;12;25 и 3;6;12;26. В каком из наборов размах больше?3.Дан набор чисел: 3;5;7. Какое число надо к нему добавить, чтобы размах нового набора стал равен 95.
4.К набору 3;4;5 добавьте ещё одно число, чтобы его наибольшее значение не изменилось.
а) выполните требование задачи так, чтобы размах остался прежним.
б) выполните требование задачи так, чтобы размах стал больше.
Слайд 30 Самостоятельная работа «Среднее арифметическое».
1.На координатной прямой отметьте точки 2;3;7
и их среднее арифметическое.
2.Добавьте к набору чисел 2;3;7 такое число,
чтобы среднее арифметическое осталось прежним.3. .Добавьте к набору чисел 2;3;7 такое число, чтобы среднее арифметическое стало равным 5.
4.Среднее арифметическое чисел 85;25;68;78 равно 64. Найдите:
а) среднее арифметическое - 85; - 25; - 68; - 78;
б) среднее арифметическое 170;50;136;156;
в) среднее арифметическое 80;20;63;73.
5. В первенстве школы по футболу команда 7А класса провела 17 матчей и забила 32 гола, пропустив при этом 15 мячей. Сколько мячей в среднем попадало в ворота противников этой команды за каждую игру в школьном первенстве?
Слайд 31 Самостоятельная работа «Медиана. Мода».
1. Найдите медианы наборов чисел:
686;478;834;706;843;698;549
686;478;834;706;843;698;549;112.2. Дан набор, в котором число 3 встречается 1 раз, число 4 – десять раз, а число 5 – сто раз. Других чисел в наборе нет. Укажите медиану данного набора.
3. Измеряя вес семи пришедших на урок учеников, учитель физкультуры получил ряд чисел: 51,53,59,52,55,54,51. Найдите разность между модой и медианой данного ряда.
4. В трёх баскетбольных командах измерили рост игроков. В первой команде средний рост составил 195 см, во второй команде медиана ростов равна 197 см, а в третьей команде самый низкий спортсмен имеет рост 192 см. В каждой команде 7 игроков. Из этих команд решено набрать новую команду, рост игроков в которой не меньше 193 см. Сколько человек наверняка попадут в эту команду?
Теги