Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фракталы
Содержание
- 1. Фракталы
- 2. Математика, если на нее правильно посмотреть,
- 3. Фракталы в природе
- 4. Понятие "фрактал".Понятия фрактал и фрактальная геометрия, появившиеся
- 5. Роль фракталов в машинной графике сегодня достаточно
- 6. Геометрические фракталы. Геометрические фракталыИменно с них и
- 7. Снежинка КохаИз геометрических фракталов очень интересным и
- 8. Треугольник Серпинского Для построения из центра
- 9. Лист
- 10. Алгебраические фракталы. Вторая большая группа фракталов -
- 11. Множство Мандельбротаобратимся к классике - множству Мандельброта.
- 12. Для всех точек на комплексной плоскости в
- 13. Все множество Мандельброта в полной красе у
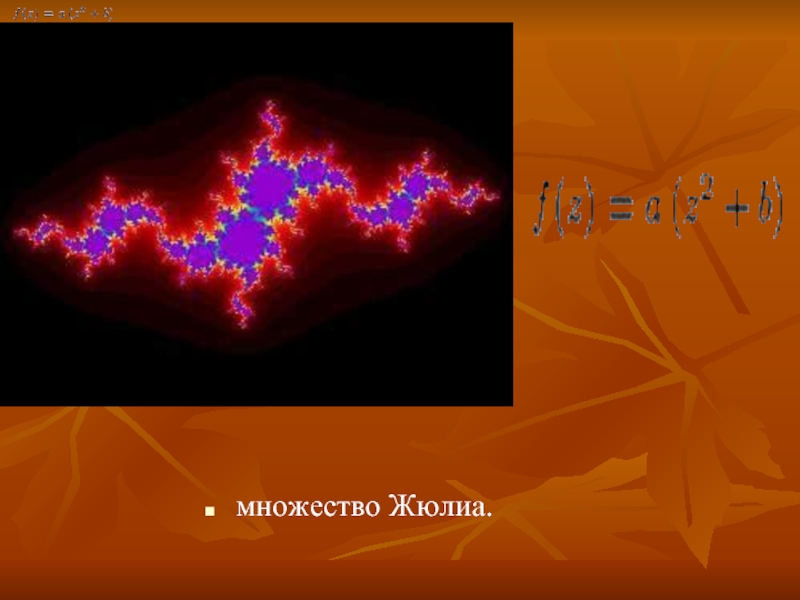
- 14. множество Жюлиа.
- 15. Галерея фракталов
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Скачать презентанцию
Математика, если на нее правильно посмотреть, отражает не только истину, но и несравненную красоту.
Слайды и текст этой презентации
Слайд 2
Математика,
если на нее правильно посмотреть,
отражает не только истину,
но и несравненную красоту.
Слайд 4Понятие "фрактал".
Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х,
с середины 80-х прочно вошли в обиход математиков и программистов.
Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую системуСлайд 5
Роль фракталов в машинной графике сегодня достаточно велика. Они приходят
на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать
линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.
Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"
Слайд 6Геометрические фракталы
. Геометрические фракталы
Именно с них и начиналась история фракталов.
Этот тип фракталов получается путем простых геометрических построений. Обычно при
построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фракталСлайд 7Снежинка Коха
Из геометрических фракталов очень интересным и довольно знаменитым является
первый - снежинка Коха. Строится она на основе равностороннего треугольника.
Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны. Получается, что наша бесконечная кривая покрывает ограниченную площадьСлайд 8Треугольник Серпинского
Для построения из центра равностороннего треугольника "вырежем" треугольник. Повторим
эту же процедуру для трех образовавшихся треугольников (за исключением центрального)
и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием.
Слайд 10Алгебраические фракталы
.
Вторая большая группа фракталов - алгебраические. Свое название они
получили за то, что их строят, на основе алгебраических формул
иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:С течением времени стремится к бесконечности.
Стремится к 0
Принимает несколько фиксированных значений и не выходит за их пределы.
Поведение хаотично, без каких либо тенденций.
Слайд 11Множство Мандельброта
обратимся к классике - множству Мандельброта.
Для его
построения нам необходимы комплексные числа. На всякий случай напомню, что
такое комплексные числа. Комплексное число - это число, состоящее из двух частей - действительной и мнимой, и обозначается оно a+bi. Действительная часть a это обычное число в нашем представлении, а вот мнимая часть bi интересней. i - называют мнимой единицей. Почему мнимой? А потому, что если мы возведем i в квадрат, то получим -1.Комплексные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень, нельзя только их сравнивать. Комплексное число можно изобразить как точку на плоскости, у которой координата Х это действительная часть a, а Y это коэффициент при мнимой части b.
Функционально множество Мандельброта определяется как Zn+1=Zn*Zn+C.
Слайд 12
Для всех точек на комплексной плоскости в интервале от -2+2i
до 2+2i выполняем некоторое достаточно большое количество раз Zn=Z0*Z0+C, каждый
раз проверяя абсолютное значение Zn. Если это значение больше 2, что рисуем точку с цветом равным номеру итерации на котором абсолютное значение превысило 2, иначе рисуем точку черного цвета. Все множество Мандельброта в полной красе у нас перед глазами.Черный цвет в середине показывает, что в этих точках функция стремится к нулю - это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. А самое интересное это границы множества. Они то и являются фрактальными. На границах этого множества функция ведет себя непредсказуемо - хаотично.
Слайд 13Все множество Мандельброта в полной красе у нас перед глазами
Справа-небольшой участок множества Мандельброта, увеличенное до размеров предыдущего рисунка.
Теги