Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции y=tgx и y=ctgx. Их свойства и графики
Содержание
- 1. Функции y=tgx и y=ctgx. Их свойства и графики
- 2. История развития тригонометрии. Первые Тригонометрические сведения были
- 3. Архимед Евклид
- 4. Название «тангенс», происходящее от латинского «tanger»
- 5. Аль-Батани Абу-ль-Вефа Мухамед-бен Мухаммед
- 6. Основные свойства функции y=tgx
- 7. Родина зарождения тригонометрии- Древняя Греция
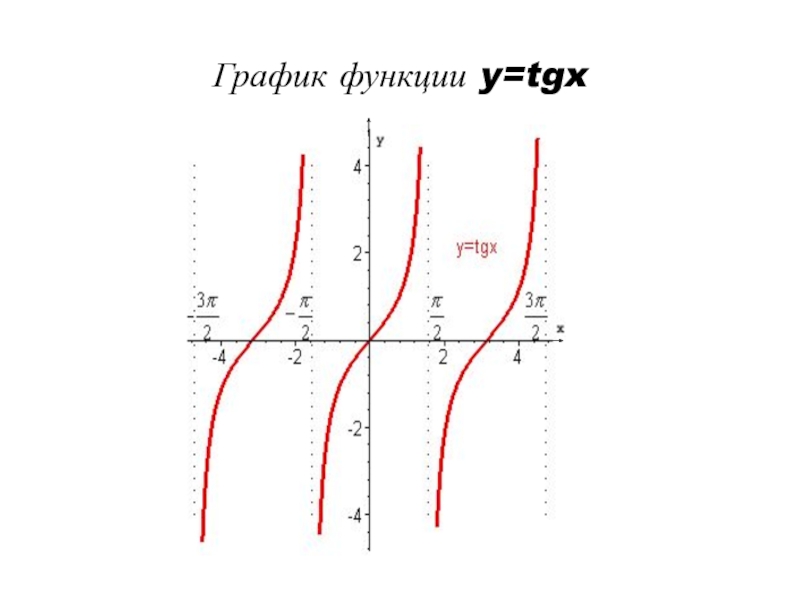
- 8. График функции y=tgx
- 9. Основные свойства функции y=ctgx
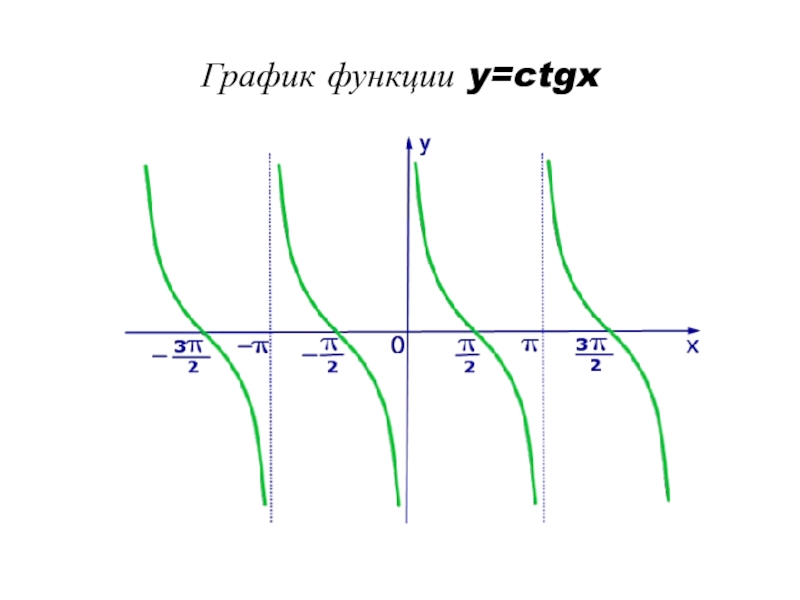
- 10. График функции y=ctgx
- 11. Графики функций y=tgx и y=ctgx
- 12. Применение Тригонометрические вычисления применяются практически во всех
- 13. Практическая часть
- 14. А)ВозрастаетБ) ВозрастаетВ) ВозрастаетГ) Возрастает
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
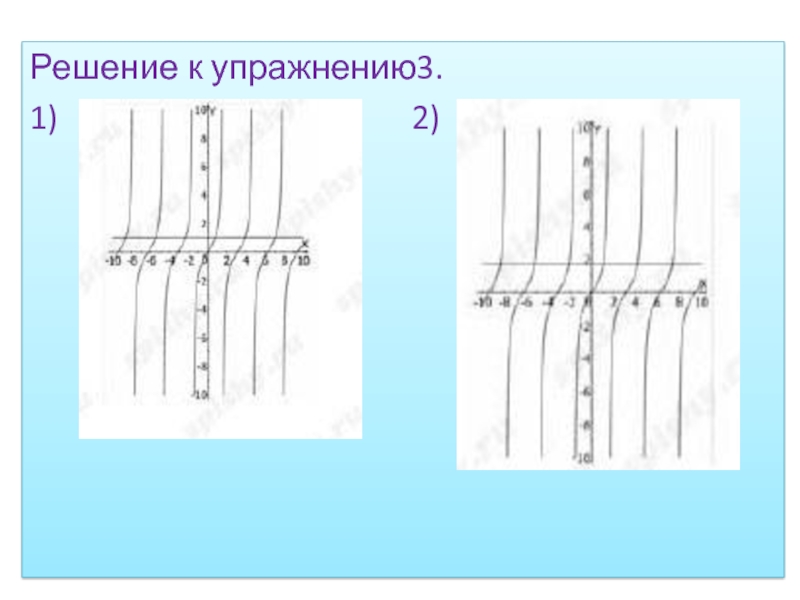
- 19. Решение к упражнению3.1)
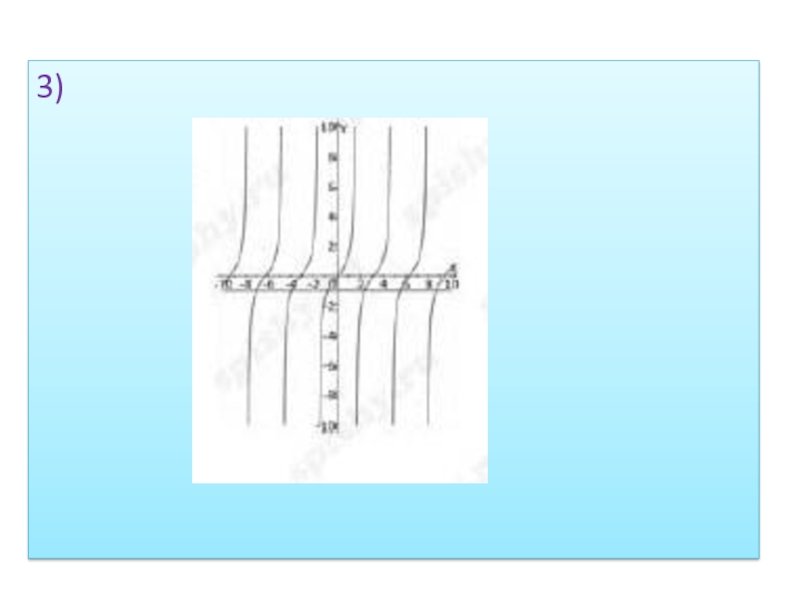
- 20. 3)
- 21. Спасибо за внимание!
- 22. Скачать презентанцию
История развития тригонометрии. Первые Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э. в работах великих
Слайды и текст этой презентации
Слайд 2История развития тригонометрии.
Первые Тригонометрические сведения были известны древним
вавилонянам и египтянам, но основы этой науки заложены в Древней
Греции встречающиеся уже в III веке до н.э. в работах великих математи- ков- Евклида, Архимеда, Апполония Пергского. Древнегреческие астро- номы успешно решали отдельные вопросы из тригонометрии, связан- ные с астрономией.
Слайд 4 Название «тангенс», происходящее от латинского «tanger» (касаться), появилось в
1583 г. Тангенсы возникли в связи с решением задачи об
определении длины тени. Тангенс (а также котангенс) введен в X веке Аль - Батани и Абу-ль-Вефа Мухамед-бен Мухаммед ,который составил таблицы синусов и тангенсов через 10`.
Слайд 12Применение
Тригонометрические вычисления применяются практически во всех областях геометрии, физики
и инженерного дела.
Большое значение имеет техника триангуляции, позволяющая измерять расстояния
до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
